Definisi, contoh dan latihan radio konvergensi diselesaikan

Dia Radius konvergensi dari satu siri kuasa adalah jejari lingkaran konvergensi yang mana siri ini menumpu. Lingkaran ini meluas dari nilai yang membatalkan asas kuasa ke singulariti terdekat fungsi yang berkaitan dengan siri ini.

Semua fungsi analisis f (z) Ia telah mengaitkan satu siri kuasa di sekitar titik bukan singular, yang dipanggil Siri Taylor:

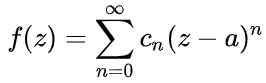
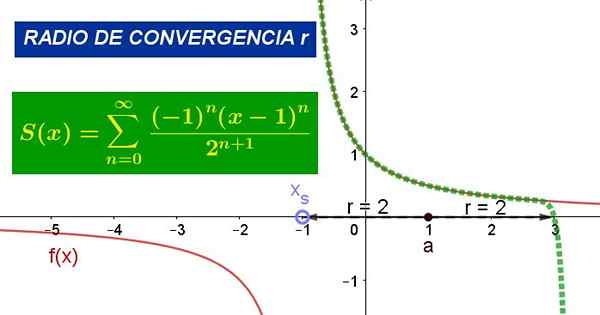
Rajah 1. Grafik menunjukkan siri kuasa sekitar nilai a = 1 untuk fungsi f (x). Jejari penumpuannya ialah r = 2. Sumber: Fanny Zapata.

Di mana ke Ia adalah pusat lingkaran penumpuan, z pemboleh ubah bebas fungsi dan c_n Mereka adalah pekali yang berkaitan dengan yang diperoleh dari fungsi F pada titik z = a.

Radius konvergensi r Ia adalah nombor sebenar positif yang mentakrifkan rantau ini:

| Z - a | < r

Di mana siri ini menumpu. Dari rantau itu siri Diverge, iaitu, ia memerlukan nilai tak terhingga. Apabila jejari konvergensi tidak terhingga, maka siri ini menumpu di seluruh satah kompleks.

[TOC]

Bagaimana radius konvergensi ditentukan?

Untuk siri yang menjadi konvergen, perlu nilai mutlak istilah berturut -turut akan berkurang apabila bilangan istilah sangat besar. Dalam cara matematik ia akan dinyatakan seperti berikut:

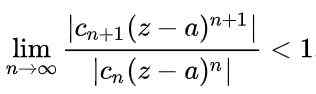
Menggunakan sifat -sifat had dalam ungkapan sebelumnya, ia diperolehi:

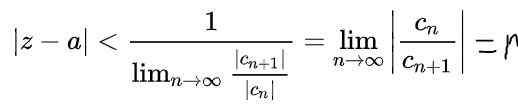
Di sini r Ia adalah jejari konvergensi dan | Z - a | < r Ia adalah bulatan sempadan terbuka di satah kompleks di mana siri ini menumpu. Sekiranya nilai ke dan pembolehubah z adalah nombor sebenar, maka selang terbuka konvergensi pada paksi sebenar akan menjadi: (A - r, a+r).

Siri Taylor

Siri Taylor fungsi f (x) Sekitar nilai ke Di mana fungsi ini mempunyai derivatif tak terhingga, ia adalah satu siri kuasa yang ditakrifkan sebagai:

Ia boleh melayani anda: Aksioma Kebarangkalian: Jenis, Penjelasan, Contoh, Latihan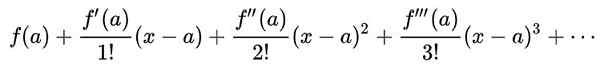

Di alam sekitar | X - a | < r, dengan r sebagaiRadius konvergensi siri, siri Taylor dan fungsi mesti f (x) Mereka bertepatan.

Sebaliknya, jejari penumpuan r Ia adalah jarak titik ke dan Singularity x_s lebih dekat ke titik ke, Menjadi titik tunggal nilai -nilai di mana had fungsi cenderung ke tak terhingga.

Iaitu, bila x → x_s Jadi F → ± ∞.

Contoh

Contoh 1

Menjadi S (x) Kuasa yang diberikan oleh ungkapan berikut:

S (x) = 1 - x + x²- x³+ x⁴-… .+(-1)ⁿ ⋅ xⁿ +… .

Untuk menentukan rantau di mana siri ini menumpu, kami mengira kuota antara istilah (n-beeimo + 1) dan istilah (n-eme):

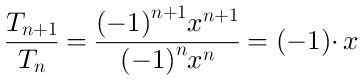
Nilai mutlak quotient anterior adalah | x | dan hadnya ketika N → ∞ ia juga  | x |.

Untuk siri ini menjadi konvergen, perlu:

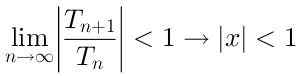
Jadi jejari konvergensi siri ini adalah R = 1, kerana ia menumpu nilai -nilai x yang berada pada jarak kurang dari 1 berkenaan dengan pusat x = 0.

Contoh 2

Anda ingin mencari siri Taylor fungsi f (x) = 1 / (1 + x) sekitar titik x = 0 dan tentukan jejari penumpuannya.

Untuk mencari siri ini, kami mengambil derivatif berturut -turut fungsi f (x), yang mana kami akan menunjukkan tiga yang pertama:

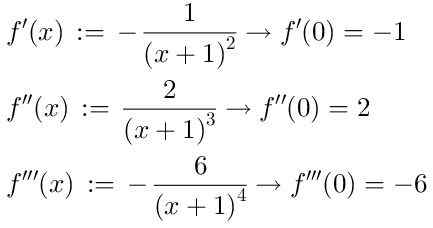
Mengambil kira bahawa istilah sifar siri siri Taylor adalah:

 f (0) = 1,

Pesanan pertama: F '(0)/1!

Pesanan kedua:

 F "(0)/2!

Pesanan Ketiga:

 f "(0)/3!

Dan sebagainya, siri Taylor fungsi yang diberikan adalah:

f (x) = 1 - x + x² - x³ + x⁴ -… .+(-1)ⁿ ⋅ xⁿ +… .

Boleh melayani anda: Segitiga sama: Ciri -ciri, sifat, formula, kawasan

Yang bertepatan dengan siri kuasa yang dikaji dalam Contoh 1.

Kami telah mengatakan bahawa jejari penumpuan siri Taylor adalah jarak dari pusat pengembangan dalam siri, yang dalam kes kami adalah nilai x = 0 sehingga keunikan pertama fungsi f (x). 

Memandangkan fungsi kami mempunyai keunikan (iaitu, tak terhingga) dalam x = -1, Jarak antara nilai -1 dan pusat pengembangan 0 adalah | -1 - 0 | = 1, Disimpulkan bahawa radius konvergensi siri Taylor adalah 1.

Hasil ini sepenuhnya bertepatan dengan yang diperolehi dalam Contoh 1 dengan kaedah lain.

Fakta bahawa zon penumpuan siri Taylor adalah selang terbuka (-1, 1) menunjukkan bahawa fungsi dan siri bertepatan dengan selang ini, tetapi tidak di luar yang sama.

Yang ditunjukkan dalam Rajah 2, di mana 41 syarat siri Taylor telah diambil, ditarik oleh garis biru yang berterusan, sementara fungsi asal ditunjukkan pada garis merah segmen.

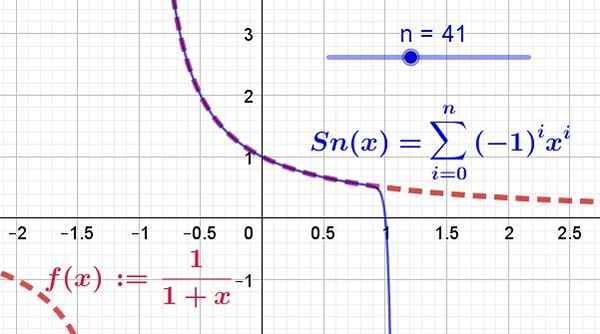Rajah 2. Fungsi f (x) (merah) dan siri kuasa (atau siri Taylor dalam warna biru) ditunjukkan. Ia dapat dilihat sebagai 41 syarat pertama siri berkumpul antara -1 dan 1. Di samping itu fungsi dan siri hanya bertepatan di rantau penumpuan. (Sumber: Fanny Zapata)

Latihan yang diselesaikan

- Latihan 1

Pertimbangkan fungsi yang sama f (x) = 1 / (1 + x) Contoh 2, tetapi kali ini diminta untuk mencari siri Taylor fungsi tersebut di sekitar titik a = 1.

Penyelesaian

Kami dapati syarat -syarat berturut -turut siri ini, bermula dengan istilah bebas iaitu f (1) = ½.

Koefisien seterusnya yang sepadan dengan istilah pesanan pertama ialah:

F '(1)/1! = -¼

Pesanan kedua ialah:

f "(1)/2! = 2/(2³ 2!)

Ikuti pekali pesanan ketiga:

Ia dapat melayani anda: Tetradecágon

F "(1)/3! = -6 / (2⁴ 3!)

Dan sebagainya. Siri Taylor akan menjadi:

SF (x) = ½ - 1/2² (X-1) + 1/2³(X-1)² - 1/2⁴ (X-1)³ + 1/2⁵ (X-1)⁴-…

- Latihan 2

Cari jejari konvergensi siri sebelumnya

Penyelesaian

Kami menulis istilah n-eme dan istilah n-alkaus lebih banyak:

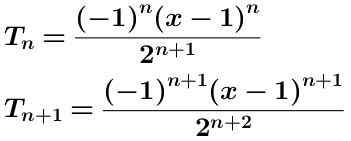Kami mengira kuota kedua -dua istilah yang ditunjukkan di bawah dipermudahkan:

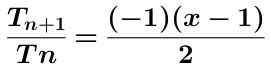
Nilai mutlak ungkapan sebelumnya diambil dengan mendapatkan:

| X - 1 | / 2

Walau bagaimanapun, untuk siri ini menjadi konvergen, adalah perlu bahawa jumlah sebelumnya adalah lebih rendah daripada unit, iaitu:

| X - 1 | < 2

Yang menunjukkan bahawa radius konvergensi di sekitar nilai x = 1 ialah:

R = 1

Sebaliknya, ungkapan sebelumnya bersamaan dengan ketidaksamaan berganda:

-2 < x - 1 < +2

Jika kita menambah +1 kepada setiap tiga ahli ungkapan sebelumnya, ia diperolehi:

-1 < x < 3

Yang merupakan selang konvergensi siri.

Rajah 1 menunjukkan fungsi asal dan siri Taylor fungsi tersebut di sekitar titik x = 1. Dalam angka itu dapat disahkan bahawa siri ini bertepatan dengan fungsi dalam persekitaran titik x = 1, tetapi dalam jejari konvergensi.

Rujukan

1. Yayasan CK-12. Siri Kuasa: Perwakilan Fungsi dan Operasi. Pulih dari: ck12.org.
2. Engler, a. 2019. Kalkulus integral. Universiti Kebangsaan Pantai.
3. Larson, r. 2010. Pengiraan pemboleh ubah. 9NA. Edisi. McGraw Hill.
4. Teks matematik percuma. Siri kuasa. Pulih dari: matematik.Liibretexts.org.
5. Wikipedia. Siri kuasa. Pulih dari: Adakah.Wikipedia.org.
6. Wikipedia. Radius konvergensi. Diperoleh dari: dalam.Wikipedia.org