Ciri -ciri Hak, Persamaan dan Contohnya

The garis serong Mereka adalah yang cenderung, sama ada berkenaan dengan permukaan rata atau garis lain yang menunjukkan alamat tertentu. Sebagai contoh, pertimbangkan tiga baris yang ditarik dalam satah yang muncul dalam angka berikut.

Kami tahu kedudukan relatif masing -masing kerana kami membandingkannya dengan garis rujukan, yang biasanya adalah X paksi yang menandakan mendatar.

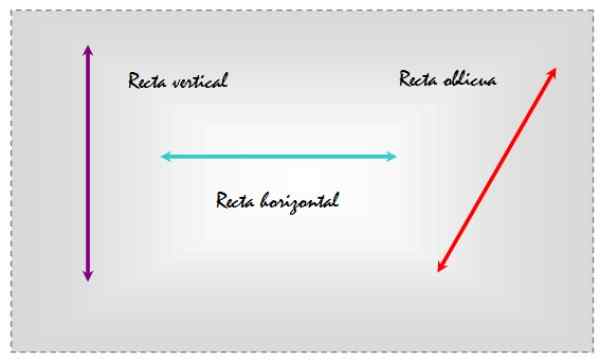
Rajah 1. Garis menegak, mendatar dan serong dalam satah yang sama. Sumber: f. Zapata.

Dengan cara ini, memilih rujukan mendatar, garis kiri adalah menegak, pusatnya mendatar dan yang di sebelah kanan adalah serong, kerana ia cenderung berkenaan dengan garis rujukan harian.

Sekarang, garis yang berada di satah yang sama, seperti permukaan kertas atau skrin, menduduki kedudukan yang berbeza antara satu sama lain, bergantung kepada sama ada mereka bersilang atau tidak. Dalam kes pertama mereka kering lurus, sementara di tempat kedua, mereka selari.

Sebaliknya, garisan pengeringan juga boleh menjadi garis lurus serong atau tegak lurus. Dalam kedua -dua kes, lereng garis adalah berbeza, tetapi garis -garis serong di antara mereka sendiri α dan β, selain 90º, manakala sudut yang ditentukan oleh garis tegak lurus sentiasa 90º.

Dalam angka berikut definisi ini diringkaskan:

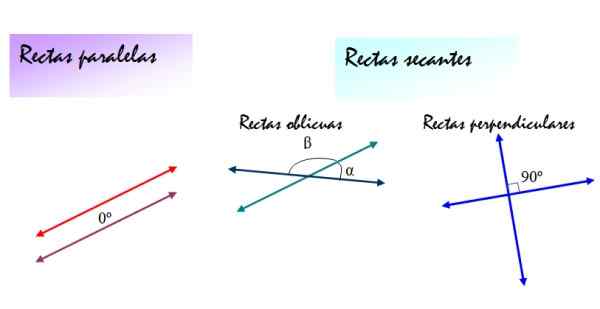Rajah 2. Kedudukan relatif antara garis: selari, serong dan tegak lurus berbeza pada sudut yang terbentuk antara satu sama lain. Sumber: f. Zapata.

[TOC]

Persamaan

Untuk mengetahui kedudukan relatif garis dalam satah, perlu mengetahui sudut yang mereka bentuk antara satu sama lain. Perhatikan bahawa garis adalah:

Boleh melayani anda: Pengiraan pendekatan menggunakan perbezaan

Selari: Sekiranya mereka mempunyai cerun yang sama (arah yang sama) dan tidak pernah bersilang, jadi mata mereka sama.

Kebetulan: Apabila semua mata mereka bertepatan dan oleh itu mempunyai cerun yang sama, tetapi jarak antara titik mereka adalah sifar.

Secantes: Sekiranya anting -anting anda berbeza, jarak antara titik mereka berbeza -beza dan persimpangan adalah satu titik.

Oleh itu, cara mengetahui jika dua baris dalam satah kering atau selari adalah melalui cerunnya. Kriteria paralelisme dan keseragaman garis adalah seperti berikut:

Menjadi dua baris l₁ dan l₂ kepunyaan pesawat, yang belum selesai masing -masing m₁ dan m₂. Garis ini selari jika m₁ = m₂ Dan mereka berserenjang ketika m₁= -1/m₂

Sekiranya mengetahui lereng dua baris dalam satah, tiada kriteria di atas dipenuhi, kami menyimpulkan bahawa garis adalah serong. Mengetahui dua titik garis, cerun dikira dengan segera, seperti yang akan kita lihat di bahagian seterusnya.

Anda boleh mengetahui sama ada dua baris kering atau selari mencari persimpangan mereka, menyelesaikan sistem persamaan yang membentuk: jika ada penyelesaiannya kering, jika tidak ada selari, tetapi jika penyelesaiannya tidak terhingga, garisnya adalah kebetulan.

Walau bagaimanapun, kriteria ini tidak memaklumkan kepada kami mengenai sudut antara garis -garis ini, walaupun mereka mempunyai persimpangan.

Untuk mengetahui sudut antara garis, dua vektor diperlukan atau dan v yang dimiliki oleh masing -masing. Oleh itu, adalah mungkin untuk mengetahui sudut yang mereka bentuk melalui produk skalar vektor, yang ditakrifkan dengan cara ini:

atau•V =atau.v.cos α

Persamaan garis dalam kapal terbang

Barisan dalam pesawat Cartesian boleh diwakili dalam beberapa cara, seperti:

Ia boleh melayani anda: Persamaan Parabola Umum (contoh dan latihan)

-Borang yang belum selesai: Yeah m Ia adalah cerun garis dan b Ia adalah persimpangan garis dengan paksi menegak, persamaan garis adalah y = mx +b.

-Persamaan umum untuk garis lurus: Kapak + oleh + c = 0, di mana M = a/b Ia adalah cerun.

Dalam satah Cartesian, garis menegak dan mendatar adalah kes -kes tertentu persamaan garis.

-Garis menegak: x = a

-Garis mendatar: y = k

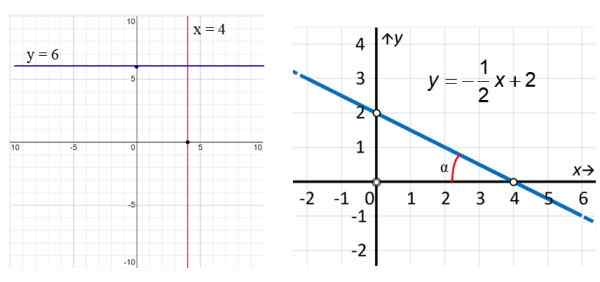Rajah 3. Di sebelah kiri garis menegak x = 4 dan garis mendatar y = 6. Di sebelah kanan contoh garis serong. Sumber: f. Zapata.

Dalam contoh Rajah 3, garis merah menegak mempunyai persamaan x = 4, manakala garis selari dengan paksi x (biru) mempunyai persamaan y = 6. Bagi garis yang betul, kita melihat bahawa ia adalah serong dan mencari persamaannya, kita menggunakan mata yang diserlahkan dalam angka: (0.2) dan (4.0) dengan cara ini:

M = (dan₂ - dan₁) / (X₂ - x₁) = (2 - 0) / (0 - 4) = - ½

Potongan garis ini dengan paksi menegak adalah y = 2, Seperti yang dinyatakan dari grafik. Dengan maklumat ini:

y = (-½) x+2

Menentukan sudut kecenderungan berkenaan dengan paksi x adalah mudah. Saya merasakan bahawa:

α = arctg (2/4) = 26.6th

Oleh itu sudut positif dari paksi x ke garisan adalah: 180º - 26.6th = 153.Ke -4

Contoh garis serong

Rajah 4. Contoh garis serong. Sumber: Ian Patterson Wrathful [CC oleh (https: // creativeCommons.Org/lesen/by/2.0)]. Menara Condong Pisa. Pixabay.

Garis serong muncul di banyak tempat, adalah masalah memberi perhatian untuk mencari mereka dalam seni bina, sukan, pendawaian bekalan elektrik, paip dan di banyak tempat. Secara semula jadi, garis serong juga hadir, seperti yang akan kita lihat di bawah:

Boleh melayani anda: peraturan derivasi (dengan contoh)

Sinar cahaya

Cahaya matahari merebak dalam garis lurus, tetapi bentuk bulat bumi mempengaruhi cara cahaya matahari mempengaruhi permukaan.

Dalam imej di bawah, kita dapat dengan jelas menghargai bahawa sinar solar mempengaruhi tegak lurus di kawasan tropika, tetapi sebaliknya mereka tiba secara serentak ke permukaan di kawasan yang sederhana dan di kutub.

Oleh itu, sinar matahari bergerak jauh lebih jauh melalui atmosfera dan juga haba merebak ke permukaan yang lebih besar (lihat angka). Hasilnya ialah kawasan yang dekat dengan tiang lebih sejuk.

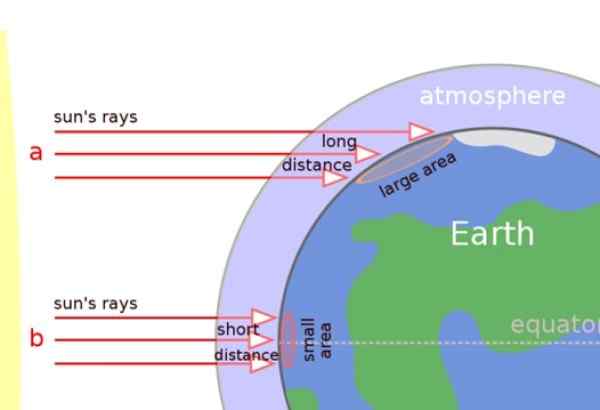Rajah 5. Sinar matahari secara serentak mempengaruhi zon sederhana dan tiang, namun mereka lebih atau kurang tegak lurus di kawasan tropika. Sumber: Wikimedia Commons.

Garis yang tidak berada dalam satah yang sama

Apabila dua baris tidak berada dalam satah yang sama, mereka masih boleh serong atau memuji, kerana mereka juga dikenali. Dalam kes ini, pengarahnya tidak selari, tetapi tidak tergolong dalam satah yang sama, garis -garis ini tidak mempunyai persimpangan.

Sebagai contoh, garis di angka yang betul jelas dalam pesawat yang berbeza. Sekiranya mereka melihat dari atas, diperhatikan bahawa mereka secara berkesan menyeberang, tetapi mereka tidak mempunyai titik yang sama. Di sebelah kanan kita melihat roda basikal, yang sinarnya kelihatan menyeberang ketika mereka melihat lurus ke depan.

Rajah 6. Garis serong yang dimiliki oleh pesawat yang berbeza. Sumber: Kiri F. Zapata, Pixabay Kanan.

Rujukan

1. Geometri. Pengarah Vektor Talian. Pulih dari: Juanbragado.adalah.
2. Larson, r. 2006. Pengiraan dengan geometri analisis. Ke -8. Edisi. McGraw Hill.
3. Matematik adalah permainan. Garis dan sudut. Pulih dari: juntadeandalucia.adalah.
4. Garis yang menyeberang. Pulih dari: Teacheraltuna.com.
5. Villena, m. Geometri analisis di R3. Diperolehi dari: DSPACE.Espol.Edu.Ec.