Matematik

Sistem koordinat segi empat tepat

Sistem koordinat segi empat tepat
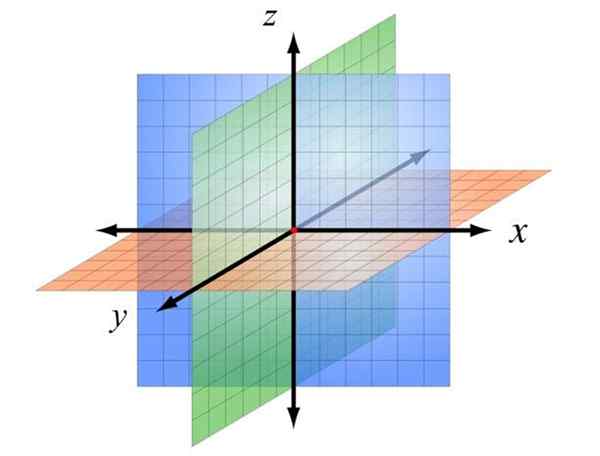
Sistem koordinat Cartesian dalam tiga dimensi. Sumber: Wikimedia Commons

Apakah sistem koordinat segi empat tepat?

Dalam Matematik dan Geometri, a Sistem koordinat segi empat tepat Ia berfungsi dengan tepat mencari titik di ruang angkasa. Untuk ini sudah cukup untuk memberikan tiga koordinat.

Pembinaan sistem dalam satah sangat mudah, hanya tiga baris yang akan menjadi paksi koordinat atau paksi Cartesian diperlukan: satu menegak, satu lagi mendatar dan ketiga yang memasuki atau meninggalkan kertas atau skrin.

Paksi ini saling berserenjang dan titik persimpangan adalah asal sistem.

Peruntukan ini ditunjukkan dalam angka di atas, di mana huruf telah diberikan kepada huruf x, dan, z, untuk membezakannya. Dengan cara ini tiga pesawat ditentukan, dengan asal berwarna merah.

Kapal terbang Xz, Berwarna biru, ia adalah satah skrin dan berada di hadapan mata pembaca. Kapal terbang Xy Ia oren, dan boleh dikaitkan dengan meja atau lantai. Akhirnya, kapal terbang zy Dalam hijau ia berserenjang dengan yang sebelumnya dan bahagian skrin atau kertas di dua wilayah.

Quadriculating setiap pesawat ini dan memberikan skala, anda boleh meletakkan titik di ruang angkasa yang memberikan koordinat masing -masing X dan z, Selalu mengikut urutan itu, untuk mengelakkan kekaburan.

Untuk apaIa melayani sistem koordinat segi empat tepat?

Sistem koordinat segi empat tepat berfungsi untuk memposisikan mana -mana titik dalam ruang atau dalam satah, cukup untuk menunjukkan tiga koordinat titik, dalam urutan x, y, z, z.

Ia boleh melayani anda: pemboleh ubah nominal: konsep dan contoh

Sekiranya titik milik pesawat, salah satu koordinat akan menjadi 0 dan jika ia berada di mana -mana paksi, dua koordinat akan menjadi 0, kecuali yang sepadan dengan lokasi titik, kecuali asal, yang, berkata sebelum ini, mempunyai koordinat (0.0.0).

Contoh berikut menjelaskan perkara di atas.

Contoh

Contoh 1

Sebarang titik P pada paksi x dinyatakan melalui koordinat p (x, 0, 0). Perhatikan bahawa asalnya, yang diserlahkan dengan warna merah dalam angka berikut, mempunyai koordinat atau (0, 0, 0).

Apabila titik di sebelah kanan asal, ia mempunyai koordinat x positif, sementara jika berada di sebelah kiri, ia adalah negatif. Sebagai contoh, P1 Blue Point mempunyai koordinat (6,0.0), manakala titik P2 dalam hijau, mempunyai koordinat (-9,0,0).

Contoh 2

Dalam angka berikut terdapat dua paksi, menjadi X paksi paksi mendatar dan Paksi y Menegak. Dengan ini sudah cukup untuk mewakili mata dalam pesawat, dua koordinat diperlukan. Asal atau titik (0.0).

Perhatikan bahawa pelupusan paksi membahagikan pesawat ke empat wilayah yang dipanggil kuadran. Paksi di atas dan di sebelah kanan asal ditetapkan dengan tanda positif, sementara di bawah dan di sebelah kiri mereka dibezakan dengan tanda negatif.

Kemudian, mata yang koordinatnya positif, sesuai dengan kuadran pertama atau kuadran i. Titik hijau mempunyai koordinat (2,3) dan berada di kuadran i.

Bagi bahagiannya, titik merah mempunyai koordinat (-3,1) dan berada di kuadran II, sementara koordinat titik biru adalah (-1.5; -2.5) dan ia berada di kuadran III.

Boleh melayani anda: pemfaktoran biasa: contoh dan latihan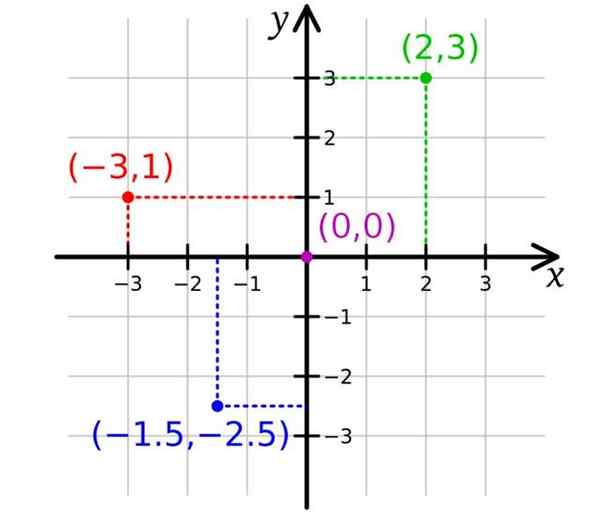 Pesawat Cartesian. Sumber: Wikimedia Commons

Contoh 3

Berikut adalah contoh titik di ruang angkasa. Koordinatnya adalah x = 6, y = 10 dan z = 8, oleh itu, p (6,10,8).

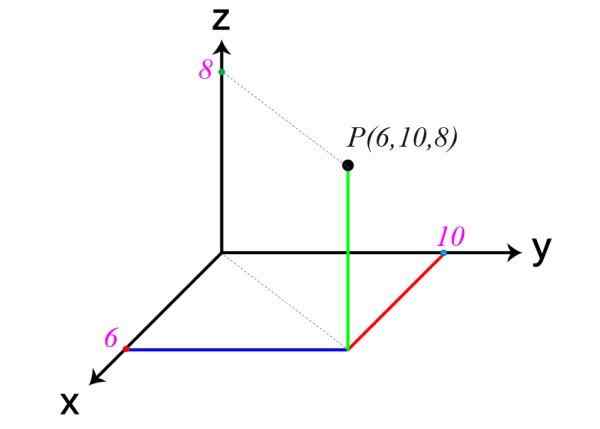Satu lagi contoh paksi Cartesian

Dalam angka permulaan, diberi amaran bahawa rancangan XY, XZ dan ZY membahagikan ruang ke dalam lapan wilayah, yang dipanggil Octavers. Titik P contohnya berada di ocant pertama.

Rujukan

  1. Alexander, d. (2013). Geometri. 5th. Edisi. Pembelajaran Cengage.
  2. Larson, r. (2012). Precalculation. Ke -8. Edisi. Pembelajaran Cengage.
  3. Stewart, J. (2007). Preccculment: Matematik untuk Pengiraan. 5th. Edisi. Pembelajaran Cengage.
  4. Pesawat Cartesian. Diperolehi dari: DL.Uncw.Edu.
  5. Weisstein, e. Koordinat Cartesian. Pulih dari: Mathworld.Wolfram.com