Kaedah Penyelesaian Persamaan, Contoh, Latihan

The Sistem Ecuation Mereka terdiri daripada dua atau lebih persamaan dengan beberapa pembolehubah yang mesti mempunyai penyelesaian yang sama. Mereka kerap, kerana dalam praktiknya terdapat banyak situasi yang bergantung kepada banyak faktor, yang berkaitan dengan beberapa cara.

Secara umum, sistem persamaan mempunyai bentuk berikut, di mana setiap fungsi mewakili salah satu syarat yang mesti dipenuhi oleh penyelesaiannya:

Rajah 1. Sistem persamaan terdiri daripada fungsi m dan n tidak diketahui. Sumber: f. Zapata.

Mari kita lihat contoh: Katakan anda perlu mengeluarkan lembaran kertas segi empat tepat yang kawasannya 180 cm² dan mempunyai perimeter 54 cm. Apa yang sepatutnya dimensi lembaran?

Untuk menjawab soalan yang kami ambil kira bahawa dimensi lembaran segi empat tepat adalah dua: lebar dan tinggi. Ini bermaksud bahawa kita mempunyai 2 pembolehubah yang akan kita berikan nama biasa x dan dan.

Dan pembolehubah ini mesti memenuhi kedua -dua syarat yang dikenakan pada masa yang sama:

-Keadaan pertama: Kawasan lamina adalah 180 cm². Ini akan menjadi fungsi pertama: f₁.

-Keadaan kedua: perimeter atau kontur lembaran mestilah 54 cm. Ini adalah fungsi kedua f₂.

Untuk setiap keadaan persamaan ditubuhkan menggunakan bahasa algebra. Kawasan A dari lembaran segi empat tepat diperoleh dengan mengalikan lebar:

A = x.y = 180 cm²

Dan perimeter P hasil daripada menambahkan sisi. Oleh kerana perimeter adalah jumlah sisi:

P = 2x + 2y = 54 cm

Sistem yang terhasil daripada dua persamaan dan dua orang yang tidak diketahui adalah:

Xy = 180

2 (x + y) = 54

Kami memerlukan dua nombor yang produknya adalah 180 dan bahawa produk berganda dari jumlahnya adalah 54, atau apa yang sama: ditambah harus memberi 27. Nombor ini adalah 12 dan 15.

Dalam bahagian Latihan yang Diselesaikan, kami akan menawarkan kaedah terperinci untuk mencari nilai -nilai ini, sementara pembaca dapat dengan mudah mengesahkan penggantian, yang berkesan memenuhi kedua -dua persamaan.

[TOC]

Contoh aplikasi sistem persamaan

Keadaan yang dicadangkan di atas mengandungi 2 pembolehubah, dan sekurang -kurangnya 2 persamaan diperlukan untuk mencari mereka. Terdapat sistem dengan banyak lagi pembolehubah, tetapi dalam apa jua keadaan, jika sistem mempunyai n Daripada jumlah ini, sekurang -kurangnya diperlukan n persamaan bebas (seseorang tidak boleh menjadi gabungan linear yang lain) untuk mencari penyelesaiannya, jika ia wujud.

Boleh melayani anda: tali (geometri): panjang, teorem dan latihan

Bagi aplikasi, mereka banyak. Berikut adalah beberapa di mana sistem persamaan menunjukkan kegunaan mereka:

-Cari arus yang beredar melalui litar melalui undang -undang Kirchoff.

-Di tanah dan pengangkutan udara untuk menetapkan jadual keluar dan ketibaan.

-Cari magnitud daya dalam sistem dinamik atau statik tertakluk kepada pelbagai interaksi.

-Untuk mengetahui jumlah item yang dijual untuk jangka waktu tertentu, atau di kilang -kilang, untuk menentukan dimensi objek untuk memenuhi syarat -syarat tertentu dari segi permukaan atau kelantangan.

-Semasa menentukan cara mengedarkan modal dalam beberapa pelaburan.

-Menetapkan kadar untuk pelbagai perkhidmatan, contohnya telekomunikasi atau menunjukkan dan ketahui jumlah wang yang dikumpulkan (lihat contoh diselesaikan 2)

Kaedah Penyelesaian Sistem Persamaan

Kaedah penggantian

-Persamaan dipilih dan salah satu pembolehubah dibersihkan.

-Kemudian anda perlu mengganti pemboleh ubah yang jelas dalam persamaan lain. Maka pembolehubah ini hilang dari sana dan jika sistem mempunyai dua persamaan dan dua orang yang tidak diketahui, ada persamaan dengan pembolehubah yang sudah jelas.

-Sekiranya sistem mempunyai lebih daripada dua pembolehubah, anda perlu membersihkan satu pertiga yang tidak diketahui dari persamaan lain dan menggantinya juga.

Contoh permohonan kaedah ini adalah pada tahun yang diselesaikan 1.

Kaedah pengurangan atau penghapusan

Kaedah ini terdiri daripada menambah atau menolak persamaan untuk menghapuskan satu atau lebih pembolehubah dan meninggalkan satu. Untuk melakukan ini, mudah untuk membiak persamaan dengan faktor seperti itu dengan menambahkan dengan persamaan lain, yang tidak diketahui hilang. Mari lihat contoh:

3x² - dan² = 11

Boleh melayani anda: Langkah -langkah kecenderungan pusat untuk data dikumpulkan: formula, latihan

x² + 4y² = 8

Kami membiak persamaan pertama dengan 4:

12x² - 4y² = 44

x² + 4y² = 8

Dengan menambahkan mereka yang tidak diketahui hilang dan, Menginap:

13x² = 52

x² = 4

Oleh itu x₁ = 2 dan x₂ = -2. Dengan nilai -nilai ini pembaca dapat mengesahkannya dan₁ = 1 dan₂ = -1

Kaedah penyamaan

Apabila sistem adalah dua persamaan dengan dua orang yang tidak diketahui:

-Yang tidak diketahui dipilih dan membersihkan kedua -dua persamaan.

-Hasilnya disamakan, yang membolehkan untuk mendapatkan satu persamaan dengan satu yang tidak diketahui.

-Persamaan ini diselesaikan dan hasilnya digantikan di salah satu penjelasan sebelumnya untuk mendapatkan nilai yang lain yang tidak diketahui.

Kaedah ini akan digunakan pada tahun yang diselesaikan 2 bahagian berikut.

Kaedah grafik

Kaedah ini terdiri daripada grafik lengkung yang setiap persamaan mewakili. Titik persimpangan adalah penyelesaian sistem. Contoh berikut menunjukkan penyelesaian grafik sistem:

x² + dan ² = 1

2x + 4y = 0

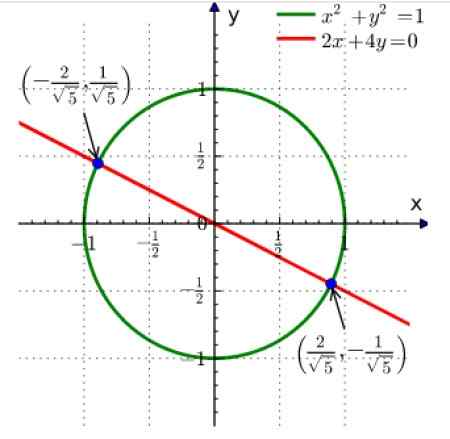Rajah 2. Penyelesaian grafik sistem persamaan serentak adalah untuk mencari persimpangan lengkung. Sumber: Wikimedia Commons.

Yang pertama persamaan adalah bulatan radius 1 yang difokuskan pada asal dan yang kedua adalah garis.

Persimpangan kedua -duanya adalah dua mata yang ditunjukkan dengan warna biru. Pembaca dapat mengesahkan bahawa dengan menggantikan koordinat mata dalam persamaan di atas, kesamaan diperolehi.

Latihan

- Latihan diselesaikan 1

Anda perlu mengeluarkan lembaran segi empat tepat di kawasan 180 cm² dan dengan perimeter 54 cm. Apa yang sepatutnya dimensi lembaran?

Penyelesaian

Sistem yang perlu diselesaikan adalah:

Xy = 180

2 (x + y) = 54

Persamaan kedua dapat dipermudahkan ke x + y = 27, oleh itu:

Xy = 180

x + y = 27

Salah satu yang tidak diketahui persamaan kedua dibersihkan:

y = 27 - x

Pelepasan digantikan pada yang pertama:

(27 -x) = 180

Memohon harta pengedaran:

-x² + 27x = 180

Mengalikan dengan (-1) di kedua-dua belah persamaan dan menghantar 180 ke sebelah kiri:

x² - 27x +180 = 0

Ia adalah persamaan darjah kedua dalam x, yang diselesaikan oleh formula:

Ia dapat melayani anda: sudut bertentangan dengan puncak (dengan senaman yang diselesaikan)

Dengan a = 1, b = -27 dan c = 180

 Penyelesaiannya adalah: x₁ = 15 cm dan x₂ = 12, oleh itu dimensi y adalah dan₁ = 12 cm dan dan₂ = 15 cm.

- Latihan diselesaikan 2

Taman hiburan mempunyai kadar berikut setiap pintu masuk: kanak -kanak 1.5 dan orang dewasa $ 4. Dalam satu hari terdapat 2200 pelawat, menaikkan $ 5050. Cari bilangan kanak -kanak dan orang dewasa yang melawat taman pada hari itu.

Rajah 3. Sistem persamaan berfungsi untuk memecah koleksi taman hiburan dalam sehari. Sumber: Pixabay.

Penyelesaian

Menjadi x Jumlah anak dan dan Bilangan orang dewasa. Kita boleh menubuhkan yang pertama persamaan mengetahui bahawa jumlah kedua -duanya mestilah 2200:

x + y = 2200.

Sekarang kita pergi dengan wang yang dikumpulkan. Harga tiket untuk kanak -kanak adalah 1.5 $ untuk setiap kanak -kanak, dengan mengalikan nilai ini dengan x, bilangan kanak -kanak, kami akan mempunyai jumlah untuk kemasukan kanak -kanak:

1.5x = wang yang dibangkitkan oleh tiket kanak -kanak

Dan jika kita melipatgandakan $ 4 setiap orang dewasa untuk pengunjung kuantiti dan dewasa, jumlah wang diperoleh oleh semua orang dewasa:

4y = wang yang dibangkitkan oleh tiket dewasa

Kami menambah ini untuk mendapatkan $ 5050:

1.5x + 4y = 5050

Sistem persamaan kami adalah:

x + y = 2200

1.5x + 4y = 5050

Mari kita selesaikannya dengan menyamakan kedudukan. Kami membersihkan pemboleh ubah dan persamaan pertama dan kedua:

y = 2200 - x

y = (5050 - 1.5 x) /4

Kami sama dengan kedua -dua ungkapan:

2200 - x = (5050 - 1.5x) /4

Kami mengalikan segala -galanya dengan 4 untuk menghapuskan pecahan:

8800 - 4x = 5050 - 1.5x

Kami mengumpulkan istilah dengan x di sebelah kiri dan nombor tulen di sebelah kanan:

-4x + 1.5x = 5050 - 8800

-2.5x = -3750

x = 1500 kanak -kanak.

Kami menggantikan nilai ini pada y = 2200 - x untuk mengetahui bilangan orang dewasa:

y = 2200 - 1500 = 700 orang dewasa.

Rujukan

1. CK-12. Sistem persamaan dan ketidaksamaan. Pulih dari: ck12.org.
2. Hoffman, J. Pemilihan masalah matematik. Jilid 2.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Stewart, J. 2006. Preccculment: Matematik untuk Pengiraan. 5th. Edisi. Pembelajaran Cengage.
5. Zill, d. 1984. Algebra dan trigonometri. McGraw Hill.