Mereka adalah segmen rectilineal yang mungkin dalam setiap poligon

Pepenjuru persegi

Segmen rectilineal yang mungkin dalam setiap poligon adalah Diagonal. Diagonal adalah segmen garisan yang ditarik dengan menyertai dua simpul yang tidak bersekongkol dari poligon. Dalam erti kata lain, garis pepenjuru bermula pada puncak angka dan berakhir dengan yang lain yang tidak akan datang.

Dalam imej di atas, pepenjuru persegi ditunjukkan dalam strok hitam, yang dapat dilihat, bergabung dengan dua sudut bertentangan.

Diagonal dari persegi mengukur sama, tetapi dalam rombus, dua pepenjuru mereka berbeza, ada yang lebih besar, lebih lama, dan lebih pendek, lebih pendek.

Cara mengira bilangan pepenjuru poligon?

Menentukan bilangan pepenjuru poligon boleh menjadi mudah ketika datang ke persegi atau rombus, tetapi sebagai bilangan sisi angka meningkat, ia menjadi lebih rumit untuk memvisualisasikan berapa banyak pepenjuru yang ada.

Inilah sebabnya formula mudah yang akan menjadikan proses ini lebih efisien digunakan dalam matematik:

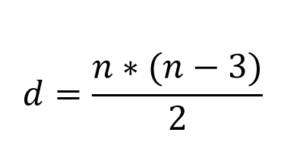
Harus diingat bahawa n adalah sama dengan bilangan sisi poligon, dan n mestilah lebih besar daripada 3. Kerana? (Terus membaca, jawapannya pada akhirnya).

Contoh 1

Kirakan jumlah pepenjuru octagon.

Octagon adalah poligon lapan orang biasa, ini bermaksud bahawa semua sisi dan sudut dalamannya sama.

Menggunakan formula sebelumnya, sudah cukup untuk menggantikan N selama lapan:

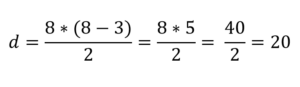
Dengan cara ini diketahui bahawa bilangan pepenjuru yang boleh diambil dari simpul poligon oktagon adalah 20.

Ia boleh melayani anda: media berwajaran: bagaimana ia dikira, contoh dan latihan

Tanpa formula, mungkin rumit untuk cuba mengira semua pepenjuru, bahkan mempunyai lukisan yang baik. Dan semakin tinggi jumlah sisi pada angka itu, semakin rumitnya.

Contoh 2

Kirakan panjang pepenjuru segi empat tepat dengan teorem pythagora.

Teorem Pythagoras menegaskan bahawa jumlah kuadrat kategori segitiga segi empat tepat, yang dipanggil A dan B, bersamaan dengan kuadrat hipotenus (sisi bertentangan dengan sudut kanan), yang dipanggil c.

Dalam notasi algebra ia akan menjadi:

ke² + b² = c²

Diagonal dari segi empat tepat membentuk segitiga segi empat tepat, yang boleh menggunakan teorem ini, di mana b adalah asas dan h ialah ketinggian.

Jika asasnya adalah 12 cm dan ketinggiannya adalah 7 cm, apabila menggantikannya adalah:

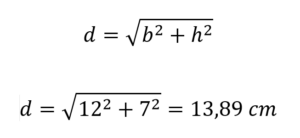
Oleh itu, panjang pepenjuru segi empat tepat adalah 13.89 sentimeter.

Poligon tanpa pepenjuru

Adakah mungkin ada poligon yang tidak mempunyai garis pepenjuru? Bagaimana keadaannya?

Teka -teki ini boleh digunakan untuk menembak rasa ingin tahu pada kanak -kanak dan menjadikannya menggambarkan pepenjuru angka:

Segitiga adalah poligon tiga -sisi dan mempunyai tiga sudut dalaman. Tetapi ia tidak mempunyai pepenjuru

Ya, segitiga tidak mempunyai pepenjuru.

Penjelasan

Segitiga adalah poligon tiga yang mempunyai tiga sudut dalaman. Tetapi segitiga adalah angka cembung yang tidak mempunyai garis pepenjuru, menjadi poligon matematik yang paling mudah dan paling menarik.

Kelihatan baik pada formula yang membolehkan anda mengira pepenjuru poligon:

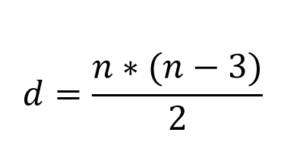
Ia segera diperhatikan bahawa dengan menggantikan n = 3, ia diperolehi sebagai hasil d = 0. Iaitu, segitiga tidak mempunyai pepenjuru, tidak ada cara untuk melukis. Tetapi poligon dengan n = 4, misalnya, mempunyai dua pepenjuru.

Boleh melayani anda: Decagon: biasa, tidak teratur, sifat, contoh