Jumlah sejarah, formula dan sifat Riemann, Latihan

The Riemann Sum Adalah nama yang menerima pengiraan anggaran integral yang ditetapkan, dengan jumlah yang bijak dengan nombor terma terhingga. Permohonan biasa adalah pendekatan kawasan fungsi dalam grafik.

Ia adalah ahli matematik Jerman Georg Friedrich Bernhard Riemann (1826-1866) yang ditawarkan untuk pertama kalinya definisi yang ketat tentang integral fungsi dalam selang waktu tertentu. Dia mengumumkannya dalam artikel yang diterbitkan pada tahun 1854. 

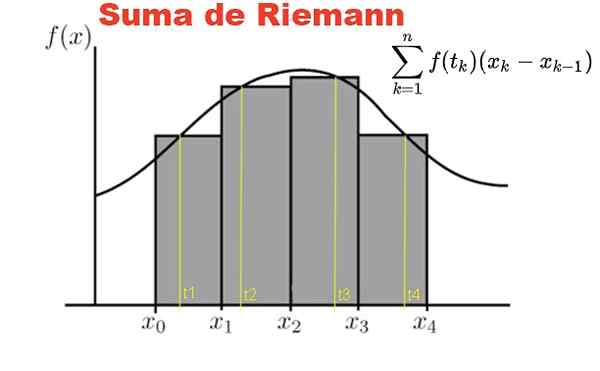
Rajah 1. Jumlah Riemann ditakrifkan pada fungsi F dan partition dalam selang [x0, x1]. Sumber: Fanny Zapata.

Jumlah Riemann ditakrifkan pada fungsi y = f (x), dengan x milik selang tertutup [a, b]. Pada selang ini partition p of n elements dibuat:

P = x₀= a, x₁, x₂,..., x_n= b

Ini bermakna bahawa selang dibahagikan seperti berikut:

 Di sini t_k adalah antara x_K-1 dan x_k:

x_K-1 ≤ t_k ≤ x_k

Rajah 1 menunjukkan jumlah riemann fungsi f dalam selang [x₀, x₄] Pada partition empat subintervals, segi empat tepat kelabu.

Jumlahnya mewakili jumlah kawasan segi empat tepat dan hasil jumlah ini adalah pendekatan berangka ke kawasan di bawah lengkung F, di antara abscissas x = x₀ y x = x₄.

Sudah tentu, pendekatan ke kawasan di bawah lengkungnya sangat bertambah baik sehingga jumlahnya n partition lebih besar.  Dengan cara ini jumlahnya menumpu ke kawasan di bawah lengkung, ketika nombornya n Partition cenderung ke tak terhingga.

[TOC]

Formula dan sifat

Riemann's Jumlah F (x) Riemann pada partition:

Boleh melayani anda: rhomboid: ciri -ciri, cara mengeluarkan perimeter dan kawasan

P = x₀= a, x₁, x₂,..., x_n= b

Ditakrifkan pada selang [a, b], ia diberikan oleh:

S (p, f) = Σ_{K = 1}ⁿ f (t_k) (x_k - x_K-1) 

Di mana t_k Ia adalah nilai dalam selang [x_k, x_K-1]. Dalam jumlah Riemann, selang lebar lebar biasanya digunakan Δx = (b - a)/n, di mana a dan b adalah nilai minimum dan maksimum abscissa, manakala n adalah bilangan subdivisi.

Dalam hal ini Jumlah kanan Riemann adalah:

SD (f, n) = [f (a+Δx)+f (a+2Δx)+...+f (a+(n-1) Δx)+f (b)]*Δx

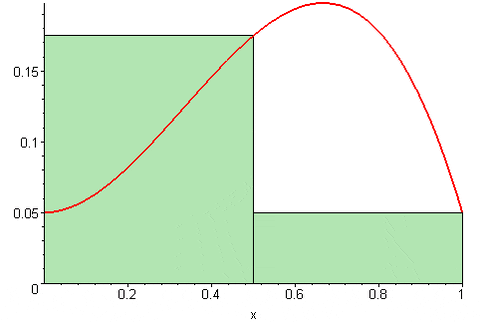Rajah 2. Jumlah kanan Riemann. Sumber: Wikimedia Commons. 09GlasGow09 [CC BY-SA (https: // creativeCommons.Org/lesen/by-sa/3.0)].

Sementara Jumlah kiri Riemann Ia dinyatakan sebagai:

Ya (f, n) = [f (a)+f (a+Δx)+...+f (a+(n-1) Δx)]*Δx

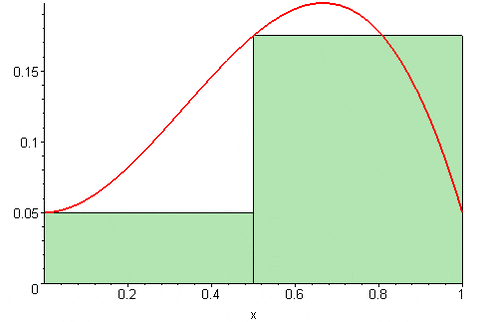Rajah 3. Jumlah Riemann pergi. Sumber: Wikimedia Commons. 09GlasGow09 [CC BY-SA (https: // creativeCommons.Org/lesen/by-sa/3.0)]

Akhirnya Riemann Central Sum adalah:

Sc (f, n) = [f (a+Δx/2)+f (a+3Δx/2)+...+f (b- Δx/2)]*Δx

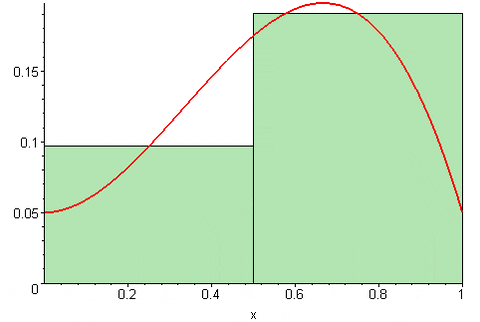Rajah 4. Jumlah Perantaraan Riemann. Sumber: Wikimedia Commons. 09GlasGow09 [CC BY-SA (https: // creativeCommons.Org/lesen/by-sa/3.0)]

Bergantung pada tempat t terletak_k Dalam selang [x_k, x_K-1] Jumlah Riemann dapat menaksir atau meremehkan nilai tepat kawasan di bawah lengkung fungsi y = f (x) (x). Iaitu, segi empat tepat dapat cemerlang dari lengkung atau sedikit di bawah ini.

Kawasan di bawah lengkung

Harta utama jumlah Riemann dan yang pentingnya menjadi, adalah bahawa jika bilangan subdivisi cenderung kepada tak terhingga, hasil dari jumlah itu menumpu kepada integral fungsi yang ditetapkan:

Ungkapan sebelumnya sepadan dengan definisi integral Riemann dan terpakai dengan syarat fungsi f berterusan dan lembut. Untuk lebih banyak fungsi tertentu terdapat definisi lain yang penting (Integral de Stieldjes dan Integral de Lebesgue).

Ia boleh melayani anda: ralat anggaran standard: Bagaimana ia dikira, contoh, latihan

Latihan yang diselesaikan

- Latihan 1

Kirakan nilai integral yang ditakrifkan antara a = -2 hingga b = +2 fungsi:

f (x) = x²

Gunakan sejumlah Riemann. Untuk melakukan ini, cari jumlah untuk partisi tetap selang [a, b] dan kemudian ambil had matematik untuk kes bahawa bilangan partition menyimpan ke tak terhingga. 

Penyelesaian

Ini adalah langkah -langkah untuk diikuti:

-Pertama, selang partition ditakrifkan sebagai: 

Δx = (b - a)/n. 

-Kemudian jumlah Riemann di sebelah kanan sepadan dengan fungsi f (x) adalah seperti ini:

-Sekarang mereka diganti A = -2 dan B =+2, supaya selang atau langkah Δx = 4/n. Maksudnya bahawa jumlah Riemann untuk fungsi f (x) = x² adalah:

-Kemudian binomial persegi dibangunkan: 

[-2 +(4i/n)]² = 4 - (16 i /n) + (4 /n)² Yo²

-Dan kemudian ia digantikan dengan teliti dalam jumlah:

-Langkah seterusnya adalah untuk memisahkan ringkasan dan keluarkan jumlah malar sebagai faktor umum bagi setiap jumlah. Adalah perlu untuk mengambil kira bahawa indeks itu adalah saya, oleh itu angka dan syarat dengan n Mereka dianggap tetap:

-Setiap jumlah dinilai, kerana bagi masing -masing terdapat ungkapan yang sesuai. Sebagai contoh, yang pertama ringkasan da n:

Yang kedua ialah:

 Dan yang ketiga ialah:

 -Menggantikan hasil ringkasan dalam jumlah Riemann, akhirnya diperoleh:

S (f, n) = 16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n²

-Akhirnya anda perlu mengira integral adalah:

= lim_N➝∞ [16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n²] =

= 16 -(64/2) + (64/3) = 16/3 = 5.333

Pembaca dapat mengesahkan bahawa ini adalah hasil yang tepat, yang dapat diperoleh dengan menyelesaikan integral dan menilai batas integrasi oleh peraturan barrow.

Boleh melayani anda: Cara menukar dari km/h a m/s? Latihan yang diselesaikan

- Latihan 2

Tentukan kira -kira kawasan di bawah fungsi: 

f (x) = (1/√ (2π) e^(-x2/2)

Antara x = -1 dan x =+1, menggunakan jumlah pusat Riemann dengan 10 partition. Bandingkan dengan hasil yang tepat dan anggaran perbezaan peratusan.

Penyelesaian

Langkah atau peningkatan antara dua nilai diskret berturut -turut adalah:

Δx = (1 - (-1)/10 = 0.2

Supaya partition p di mana segi empat tepat ditakrifkan adalah seperti ini:

P = -1,0; -0.8; -0,6; -0.4; -0,2; 0.0; 0.2; 0.4; 0.6; 0.8; 1.0

Tetapi seperti yang anda mahukan adalah jumlah pusat, fungsi f (x) akan dinilai pada pertengahan titik subintervals, iaitu dalam set:

T = -0.9; -0.7; -0.5; -0,3; -0,1; 0.1; 0.3; 0.5; 0.7; 0.9.

Jumlah Riemann (tengah) seperti ini:

S = F (-0.9)*0.2 +F (-0.7)*0.2 +F (-0.5)*0.2 +... +F (0.7)*0.2 +F (0.9)*0.2

Oleh kerana fungsi F adalah simetri, adalah mungkin untuk mengurangkan jumlahnya hanya 5 istilah dan hasilnya didarabkan oleh dua:

S = 2*0.2*f (0.1)+ F (0.3)+ F (0.5)+ F (0.7)+ F (0.9)

S = 2*0.2*0.397+ 0.381+ 0.352+ 0.312+ 0.266 = 0.683

Fungsi yang diberikan dalam contoh ini tidak lain adalah loceng Gauss yang terkenal (dinormalisasi, dengan purata sama dengan sifar dan sisihan piawai). Adalah diketahui bahawa kawasan di bawah lengkung dalam selang [-1,1] untuk fungsi ini adalah 0.6827.

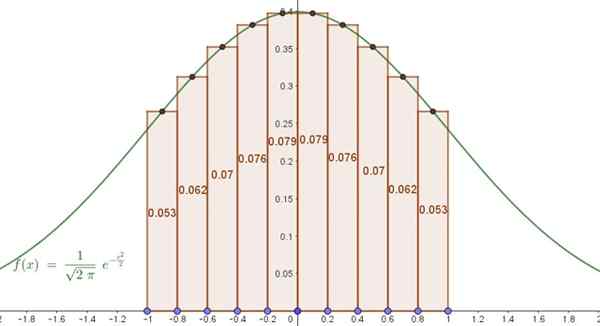Rajah 5. Kawasan di bawah loceng gauss anggaran dengan jumlah Riemann. Sumber: f. Zapata.

Ini bermakna penyelesaian anggaran dengan hanya 10 istilah bertepatan dengan penyelesaian yang tepat sehingga tiga perpuluhan. Kesalahan peratusan antara integral anggaran dan tepat ialah 0.07%.

Rujukan

1. Casteleiro, J. M., & Gómez-Alvarez, R. P. (2002). Pengiraan komprehensif (digambarkan ed.). Madrid: Editorial ESIC.
2. Unican. Sejarah konsep integral. Pulih dari: repositori.Unican.adalah
3. Uis. Riemann Sums. Pulih dari: matematik.Uis.Edu.co
4. Wikipedia. Riemann Sum. Pulih dari: Adakah.Wikipedia.com
5. Wikipedia. Integrasi Riemann. Pulih dari: Adakah.Wikipedia.com