Teorem Hijau, Demonstrasi, Aplikasi dan Latihan

Dia Teorem Hijau Ini adalah kaedah pengiraan yang digunakan untuk mengaitkan integral garis dengan kawasan ganda atau integral permukaan. Fungsi yang terlibat mesti dilambangkan sebagai vektor dan bidang yang ditakrifkan dalam trajektori c.

Sebagai contoh, ungkapan garis integral boleh menjadi sangat rumit untuk diselesaikan; Walau bagaimanapun, dalam melaksanakan teorem Green, integral berganda menjadi agak asas. Selalu penting untuk menghormati rasa positif trajektori, ini merujuk kepada arah jarum jam.

Teorem Hijau adalah kes tertentu dari Teorem Stokes, di mana unjuran fungsi vektor dijalankan dalam satah XY.

[TOC]

Definisi

Ekspresi Green teorem hijau adalah seperti berikut:

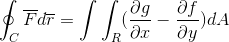
Dalam istilah pertama, garis integral yang ditakrifkan oleh trajektori "C" diperhatikan, skalar produk antara fungsi vektor "F" dan vektor "r".

C: Ini adalah trajektori yang ditakrifkan di mana fungsi vektor akan diproyeksikan selagi ia ditakrifkan untuk pesawat itu.

F: Fungsi vektor, di mana setiap komponennya ditakrifkan oleh fungsi seperti itu (f, g).

J: Ia adalah tangen vektor ke rantau r di mana integral ditakrifkan. Dalam kes ini ia dikendalikan dengan perbezaan vektor ini.

Dalam istilah kedua kita melihat teorem yang dibangunkan hijau, di mana integral ganda yang ditakrifkan di rantau r perbezaan derivatif separa G dan F diperhatikan, berkenaan dengan x dan dan masing -masing. Untuk pembezaan kawasan yang tidak lebih daripada produk kedua -dua perbezaan dimensi (dx.dy).

Teorem ini sesuai untuk integral ruang dan permukaan.

Demonstrasi

Untuk menunjukkan teorem hijau dengan cara yang mudah, tugas ini akan dipecah menjadi 2 bahagian. Pertama kita akan mengandaikan bahawa fungsi vektor f hanya mempunyai definisi dalam versor Yo. Manakala fungsi "g" sepadan dengan versor J akan sama dengan sifar.

Dapat melayani anda: berapa ratus ratus sepersepuluh? (Contoh)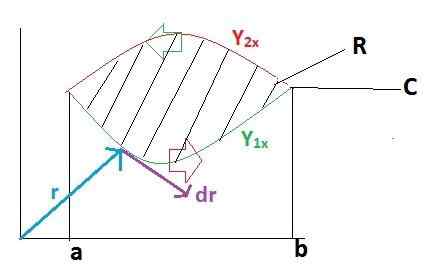Pengarang

F = f (x, y)Yo + G (x, y)J = f (x, y)Yo + 0

R = xYo + danJ

DR = DXYo + DyJ

Mula -mula kita membangunkan garis integral ke atas trajektori c, yang mana trajektori telah dikumpulkan dalam 2 bahagian yang pertama dari A ke B dan selepas B ke A.

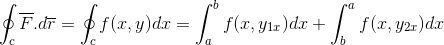
Takrif teorem asas pengiraan untuk integral yang ditetapkan digunakan.

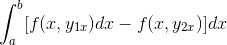
Ekspresi disusun semula dalam satu integral, dibuat sama dengan negatif dan susunan faktor -faktor yang diterbalikkan.

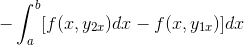
Dengan memerhatikan secara terperinci ungkapan ini, ia menjadi jelas bahawa apabila menggunakan kriteria fungsi primitif, ia adalah dengan kehadiran integral ungkapan yang diperoleh dari f berkenaan dengan dan. Dinilai dalam parameter

[Dan_1x , dan_2x]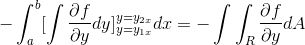

Sekarang sudah cukup untuk mengandaikan bahawa fungsi keseronokan vektor hanya ditakrifkan untuk g (x, y)J. Di mana semasa beroperasi dengan cara yang homologasi ke kes sebelumnya, ia diperolehi:

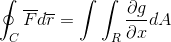
Akhirnya, demonstrasi 2 diambil dan bergabung dalam kes di mana fungsi vektor mengambil nilai untuk kedua -dua versor. Dengan cara ini ia ditunjukkan sebagai garis integral selepas menentukan dan dianggap sebagai trajektori satu dimensi, ia dapat dibangunkan sepenuhnya untuk pesawat dan ruang.

F = f (x, y)Yo + G (x, y)J

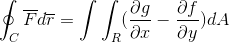
Dengan cara ini teorem hijau ditunjukkan.

Aplikasi

Aplikasi Teorema Hijau luas di cawangan fizik dan matematik. Ini meliputi sebarang permohonan atau penggunaan yang boleh diberikan kepada integrasi garis.

Kerja mekanikal yang dijalankan oleh daya F melalui trajektori C, boleh dibangunkan oleh garis integral yang dinyatakan sebagai integral ganda kawasan melalui teorem Green.

Boleh melayani anda: prisma pentagonal: ciri, bahagian, simpang, tepi, kelantangan

Momen inersia banyak badan yang tertakluk kepada daya luaran pada titik permohonan yang berlainan, juga bertindak balas terhadap integral yang boleh dibangunkan dengan teorem Green.

Ini mempunyai pelbagai fungsi dalam kajian rintangan bahan yang digunakan. Di mana nilai luaran dapat diukur dan diambil kira sebelum penjelasan pelbagai elemen.

Secara umum, teorem Green memudahkan pemahaman dan definisi bidang di mana fungsi vektor ditakrifkan berkenaan dengan rantau mengikut trajektori.

Sejarah

Ia diterbitkan pada tahun 1828 dalam kerja Analisis matematik terhadap teori elektrik dan magnet, Ditulis oleh ahli matematik British George Green. Ia meneroka bahagian yang cukup menentukan dalam penggunaan pengiraan dalam fizik, seperti konsep potensi, fungsi hijau dan aplikasi teorem auto yang bertajuk.

George Green merumuskan kerjaya pelajarnya pada usia 40 tahun, setakat ini seorang ahli matematik yang diajarkan sepenuhnya. Selepas belajar di University of Cambridge, penyelidikannya berterusan, membuat sumbangan dalam bidang akustik, optik dan hidrodinamik yang masih berkuatkuasa hari ini.

Hubungan dengan teorem lain

Teorem Hijau adalah kes khas, dan timbul dari 2 teorema yang sangat penting di cawangan pengiraan. Ini adalah teorem Kelvin-Stokes dan divergensi atau teorem Gausski.

Bermula dari mana -mana teorema anda boleh mencapai teorem hijau. Definisi dan proposisi tertentu diperlukan untuk membangunkan demonstrasi ini.

Latihan

- Latihan berikut menunjukkan cara mengubah garis integral menjadi integral ganda berkenaan dengan rantau r r.

Ekspresi asal adalah seperti berikut:

Boleh melayani anda: berapa bernilai x?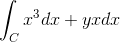

Dan mesti dinilai di rantau segi tiga yang menyertai mata (0, 0), (1, 0), (0, 1) dilambangkan oleh C. Untuk kes ini, rasa positif giliran akan dipertimbangkan.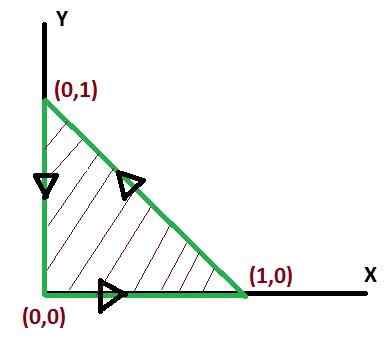

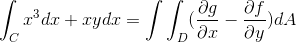
Di mana fungsi yang sepadan dengan f dan g diambil dari

f (x, y) = x³                      g (x, y) = yx

df/dy = 0 dg/dx = y

Adalah penting untuk menentukan fungsi yang membentuk had rantau C, untuk dapat memasang produk pembezaan yang akan meliputi sepenuhnya rantau ini.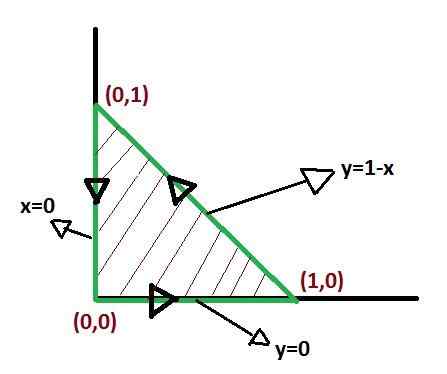

Tidak ada cara yang unik untuk menentukan had integrasi semasa menggunakan teorem hijau. Tetapi ada bentuk di mana integral setelah ditakrifkan dapat lebih mudah. Sedemikian rupa sehingga pengoptimuman had integrasi patut mendapat perhatian.

Untuk kes ini ungkapan ini dipertimbangkan: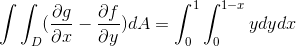

Di mana dalam menyelesaikan integral yang kita perolehi:

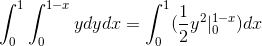
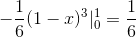
Nilai ini sepadan dengan unit padu ke rantau ini di bawah fungsi vektor dan di rantau segi tiga yang ditakrifkan oleh c.

Dalam hal garis integral tanpa melaksanakan kaedah hijau, perlu untuk memarameterkan fungsi di setiap bahagian di rantau ini. Iaitu, menjadikan 3 integral parameter untuk penyelesaian. Ini adalah bukti yang mencukupi mengenai keberkesanan yang disumbangkan oleh Robert Green dengan teoremnya kepada pengiraan.

Rujukan

1. Pengenalan kepada mekanik kontinum. W Michael Lai, David H. Rubin, Erhard Krempl, David Rubin Butterworth-Heinemann, 23 Julai. 2009
2. Kalkulus multivariable. James Stewart. Pembelajaran Cengage, 22 mar. 2011
3. Sejarah tidak rasmi teorem hijau dan idea yang berkaitan. James Joseph Cross. Jabatan Matematik, Universiti Melbourne, 1975
4. Tingkah laku haba menggunakan fungsi sayur. Kevin d. Cole, James V. Beck, a. Haji-sheikh, Bahman Luckouhi. Taylor & Francis, 16 Julai. 2010
5. Penggunaan Teorem Hijau ke Extrization of Integral Linear. Pusat Maklumat Teknikal Pertahanan, 1961