Toricelli Teorem

Apakah teorem Torricelli?

Dia Toricelli Teorem O Torricelli Prinsip menyatakan bahawa kelajuan cecair yang keluar melalui lubang di dinding tangki atau bekas, adalah sama dengan objek yang diperolehi yang jatuh secara bebas dari ketinggian yang sama dengan permukaan bebas cecair ke Lubang.

Teorem digambarkan dalam angka berikut:

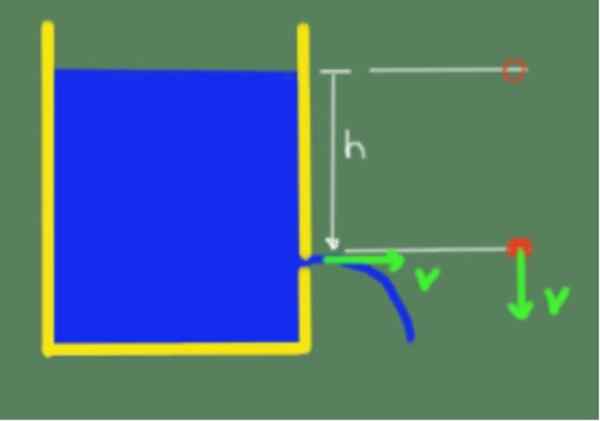Ilustrasi Teorem Torricelli. Sumber: Diri Diri.

Oleh kerana teorem Torricelli, kami dapat mengatakan bahawa kelajuan output cecair dengan lubang yang sampai ketinggian H di bawah permukaan bebas cecair diberikan oleh formula berikut:

Di mana g adalah pecutan graviti dan h ialah ketinggian dari lubang ke permukaan bebas cecair.

Penginjil Torricelli adalah ahli badan dan ahli matematik yang dilahirkan di bandar Faenza, Itali pada tahun 1608. Torricelli disebabkan oleh ciptaan barometer merkuri dan sebagai pengiktirafan terdapat unit tekanan yang dipanggil "Torr", bersamaan dengan milimeter merkuri (mm Hg).

Demonstrasi teorem

Dalam teorem Torricelli dan dalam formula yang memberikan kelajuan, ia mengandaikan bahawa kerugian yang disebabkan oleh kelikatan adalah hina, seperti dalam kejatuhan bebas, diandaikan bahawa geseran disebabkan oleh udara yang mengelilingi objek yang jatuh adalah tidak penting.

Anggapan sebelumnya adalah munasabah dalam kebanyakan kes dan juga membayangkan pemuliharaan tenaga mekanikal.

Untuk menunjukkan teorem, pada mulanya kita akan menemui formula kelajuan untuk objek yang dikeluarkan dengan kepantasan awal sifar, dari ketinggian yang sama dengan permukaan cecair di tangki.

Boleh melayani anda: Gelombang tiga -dimensi: konsep, jenis dan contoh

Prinsip pemuliharaan tenaga akan digunakan untuk mendapatkan kelajuan objek yang jatuh hanya apabila ketinggian telah jatuh h sama dengan yang dari lubang ke permukaan bebas.

Oleh kerana tidak ada kerugian geseran, adalah sah untuk menerapkan prinsip pemuliharaan tenaga mekanikal. Katakan objek yang jatuh mempunyai jisim m dan ketinggian h diukur dari tahap output bendalir.

Objek yang jatuh

Apabila objek dilepaskan dari ketinggian yang sama dengan permukaan bebas cecair, tenaganya hanya potensi graviti, kerana kelajuannya adalah sifar dan, oleh itu, tenaga kinetiknya adalah sifar. EP tenaga berpotensi diberikan oleh:

Ep = m g h

Apabila ia berjalan di hadapan lubang ketinggiannya adalah sifar, maka tenaga berpotensi adalah sifar, jadi ia hanya mempunyai tenaga kinetik yang diberikan oleh:

EC = ½ m v²

Oleh kerana tenaga dipelihara EP = EC dari apa yang diperoleh:

½ m v² = m g h

Membersihkan kelajuan v Formula Torricelli kemudiannya diperoleh:

Cecair yang keluar dari lubang

Seterusnya kita akan mendapati kelajuan output cecair melalui lubang, untuk menunjukkan bahawa ia bertepatan dengan yang hanya dikira untuk objek yang jatuh dengan bebas.

Untuk ini kita akan bergantung pada prinsip Bernoulli, yang tidak lebih dari pemuliharaan tenaga yang digunakan untuk cecair.

Prinsip Bernoulli dirumuskan seperti ini:

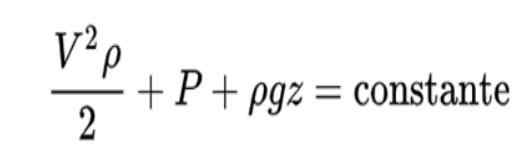
Tafsiran formula ini adalah seperti berikut:

• Istilah pertama mewakili tenaga kinetik bendalir per unit volume
• Yang kedua mewakili kerja yang dilakukan oleh tekanan per unit kawasan melintang
• Yang ketiga mewakili tenaga potensi graviti bagi setiap unit jumlah bendalir.

Boleh melayani anda: kelajuan serta -merta: definisi, formula, pengiraan dan latihan

Seperti yang kita mulakan dari premis yang merupakan cecair yang ideal, dalam keadaan tidak berkepala dengan kelajuan yang agak rendah, maka adalah penting untuk mengesahkan bahawa tenaga mekanikal per unit volum dalam bendalir adalah malar di semua wilayah atau bahagian melintang yang sama.

Dalam formula ini V adalah kelajuan cecair, ρ Ketumpatan bendalir, P tekanan dan z Kedudukan menegak.

Dalam angka yang muncul di bawah, formula Torricelli ditunjukkan berdasarkan prinsip Bernoulli.

Kami menggunakan formula Bernoulli pada permukaan bebas cecair yang kami nyatakan untuk (1) dan dalam lubang output yang kami nyatakan dengan (2). Tahap ketinggian sifar telah dipilih dengan lubang output.

Di bawah premis bahawa seksyen silang dalam (1) jauh lebih besar daripada dalam (2), kita kemudian dapat mengandaikan bahawa kelajuan penurunan cecair dalam (1) praktikal boleh diabaikan.

Inilah sebabnya V telah diletakkan₁= 0, tekanan yang cecair tertakluk dalam (1) adalah tekanan atmosfera dan ketinggian yang diukur dari lubang adalah h.

Untuk bahagian output (2) kita menganggap bahawa kelajuan output adalah v, tekanan yang cecair ke outlet juga tertakluk adalah tekanan atmosfera dan ketinggian output adalah sifar.

Nilai yang sepadan dengan bahagian (1) dan (2) digantikan dalam formula Bernoulli dan sama. Kesaksamaan adalah sah kerana kita mengandaikan bahawa cecair adalah ideal dan tidak ada kerugian geseran likat. Setelah semua istilah telah dipermudahkan, kelajuan diperolehi dalam lubang output.

Boleh melayani anda: kerdil merah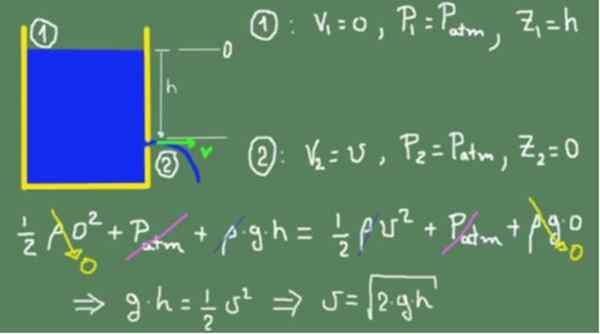

Kotak sebelumnya menunjukkan bahawa hasil yang diperoleh adalah sama dengan objek yang jatuh dengan bebas,

Dengan apa yang menunjukkan prinsip Torricelli.

Latihan yang diselesaikan

Latihan 1

Yo) Tiub saluran kecil tangki air adalah 3 m di bawah permukaan air. Kirakan kelajuan saluran air.

Penyelesaian:

Angka berikut menunjukkan bagaimana formula Torricelli digunakan untuk kes ini.

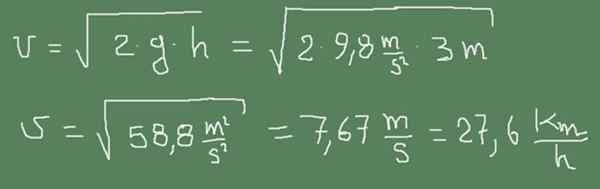
Latihan 2

Ii) Dengan mengandaikan bahawa tiub output tangki senaman sebelumnya mempunyai diameter 1 cm, hitung aliran keluar air.

Penyelesaian:

Alirannya adalah jumlah cecair yang keluar setiap unit masa, dan hanya dikira dengan mengalikan kawasan lubang output dengan kelajuan output.

Angka berikut menunjukkan butiran pengiraan.

Latihan 3

Iii) Tentukan bagaimana ketinggian permukaan air bebas dalam bekas jika diketahui

bahawa di lubang di bahagian bawah bekas, air sampai ke 10 m/s.

Penyelesaian:

Walaupun lubang berada di bahagian bawah bekas, formula Torricelli dapat digunakan.

Angka berikut menunjukkan perincian pengiraan.

Rujukan

1. Wikipedia. Toricelli Teorem.
2. Hewitt, ms. Sains Fizikal Konsep. Edisi Kelima.119.
3. Young, Hugh. 2016. Fizik Universiti Sears-Zansky dengan Fizik Moden. Edisi ke -14. Pearson. 384.