Jenis integral
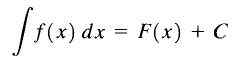
- 4279
- 1283
- Donnie Ryan
The Jenis integral bahawa kita berada dalam pengiraan adalah integral yang tidak terbatas dan integral yang ditetapkan. Walaupun integral yang ditakrifkan mempunyai lebih banyak aplikasi daripada integral yang tidak terbatas, pertama kali perlu belajar menyelesaikan integral yang tidak terbatas.
Salah satu aplikasi yang paling menarik dari integral yang ditakrifkan ialah pengiraan jumlah pepejal revolusi. Kedua -dua jenis integral mempunyai sifat linear yang sama dan juga teknik integrasi tidak bergantung kepada jenis integral.
Tetapi walaupun sangat serupa, terdapat perbezaan utama; Dalam jenis pertama integral hasilnya adalah fungsi (yang tidak spesifik) manakala dalam jenis kedua hasilnya adalah nombor.
Jenis asas integral
Dunia integral sangat luas, tetapi dalam hal ini kita dapat membezakan dua jenis integral asas, yang mempunyai kebolehgunaan yang besar dalam kehidupan seharian.
1- Integral tidak terbatas
Jika f '(x) = f (x) untuk semua x dalam domain f, kita mengatakan bahawa f (x) adalah antiderivatif, primitif atau integral f (x).
Sebaliknya, mari kita perhatikan bahawa (f (x)+c) '= f' (x) = f (x), yang menunjukkan bahawa integral fungsi tidak unik, kerana memberikan nilai yang berbeza kepada pemalar C kita akan memperoleh antiderivatif yang berbeza.
Atas sebab ini f (x)+c dipanggil integral tidak terbatas F (x) dan c dipanggil tetap integrasi dan kami menulisnya seperti berikut:
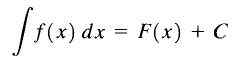 Integral tidak terbatas
Integral tidak terbatas Seperti yang dapat kita lihat, integral fungsi f (x) yang tidak terbatas adalah keluarga fungsi.
Contohnya, jika anda ingin mengira integral yang tidak terbatas pada fungsi f (x) = 3x², pertama antiderivatif f (x) mesti dijumpai terlebih dahulu.
Boleh melayani anda: trinomialSangat mudah untuk diperhatikan bahawa f (x) = x³ adalah antiderivatif, kerana f '(x) = 3x². Oleh itu, dapat disimpulkan bahawa
∫f (x) dx = ∫3x²dx = x³+c.
2- Integral yang ditakrifkan
Biarkan y = f (x) fungsi sebenar berterusan dalam selang tertutup [a, b] dan f (x) antiderivatif f (x). Ia dipanggil integral f (x) yang ditakrifkan antara had a dan b ke nombor f (b) -f (a), dan menandakan seperti berikut:
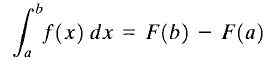 Teorem Pengiraan Fundamental
Teorem Pengiraan Fundamental Formula yang ditunjukkan di atas lebih dikenali sebagai "teorem asas pengiraan". Di sini "A" dipanggil had bawah dan "B" dipanggil had atas. Seperti yang dapat dilihat, integral pasti fungsi adalah nombor.
Dalam kes ini, jika integral f (x) = 3x² dikira dalam selang [0.3], nombor akan diperolehi.
Untuk menentukan nombor ini kita pilih f (x) = x³ sebagai antiderivatif f (x) = 3x². Kemudian, kita mengira F (3) -f (0) yang melemparkan kita sebagai hasilnya 27-0 = 27. Kesimpulannya, integral f (x) yang ditetapkan dalam selang [0.3] adalah 27.
Dapat diperhatikan bahawa jika g (x) = x³+3, maka g (x) dipilih, adalah antiderivatif f (x) yang berbeza dari f (x), tetapi ini tidak menjejaskan hasilnya sebagai g (3) -g (0) = (27+3)-(3) = 27. Atas sebab ini, dalam integral yang ditakrifkan, pemalar integrasi tidak muncul.
Salah satu aplikasi yang paling berguna bahawa jenis integral ini adalah bahawa ia membolehkan untuk mengira kawasan (jumlah) angka rata (revolusi pepejal), mewujudkan fungsi dan had integrasi yang mencukupi (dan paksi putaran).
Antara integral yang ditakrifkan, kita dapat mencari pelbagai sambungan seperti ini seperti garis integral, integral permukaan, integral yang tidak wajar, pelbagai integral, antara lain, semuanya dengan aplikasi yang sangat berguna dalam sains dan kejuruteraan.
Ia dapat melayani anda: perbezaan antara bulatan dan lilitan (dengan contoh)Rujukan
- Kishan, h. (2005). Kalkulus integral. Penerbit & Pengedar Atlantik.
- Purcell, e. J., Varberg, d., & Rigdon, s. Dan. (2007). Pengiraan (Kesembilan ed.). Prentice Hall.

