Formula menembak menegak, persamaan, contoh

Dia menembak menegak Ia adalah pergerakan yang berlaku di bawah tindakan bidang kuasa, biasanya graviti, dapat naik atau turun. Ia juga dikenali dengan nama Pelancaran menegak.

Contoh paling segera dibuang (atau turun jika disukai) bola dengan tangan anda, ya, pastikan untuk melakukannya secara menegak. Menghina rintangan udara, pergerakan yang mengikuti bola sesuai dengan model pergerakan rectilinear yang bervariasi seragam (MRUV).

Rajah 1. Bercakap bola secara menegak adalah contoh pukulan menegak yang baik. Sumber: Pexels.

Penangkapan menegak adalah pergerakan yang banyak dikaji dalam kursus pengantar fizik, kerana ia adalah contoh dari pergerakan dalam dimensi, Model yang sangat mudah dan berguna.

Model ini bukan sahaja boleh digunakan untuk mengkaji kinematik objek di bawah tindakan graviti, tetapi juga, seperti yang akan dilihat kemudian, menggambarkan pergerakan zarah di tengah -tengah medan elektrik seragam.

[TOC]

Formula dan persamaan

Perkara pertama yang diperlukan adalah sistem koordinat untuk menunjukkan asal dan labelkannya dengan huruf, yang dalam hal pergerakan menegak adalah huruf "dan".

Maka rasa positif dipilih +dan, yang biasanya naik dan makna -dan yang biasanya diturunkan (lihat Rajah 2). Semua ini melainkan siapa yang menyelesaikan masalah memutuskan sebaliknya, kerana pilihan lain adalah dengan positif arah arah pergerakan, apa pun ini.

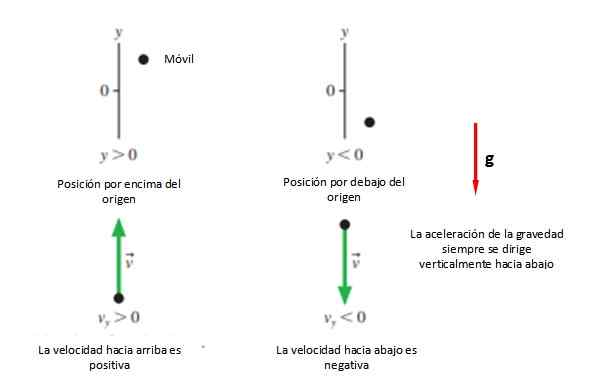Rajah 2. Konvensyen Tanda Biasa dalam Pukulan Menegak. Sumber: f. Zapata.

Walau apa pun, disarankan bahawa asalnya bertepatan dengan titik pelancaran dan_{Sama ada}, Kerana persamaan dipermudahkan, walaupun kedudukan yang dikehendaki dapat diambil untuk mulai mempelajari pergerakan tersebut.

Ia boleh melayani anda: Keadaan Keseimbangan Kedua: Penjelasan, Contoh, Latihan

Persamaan menembak menegak

Setelah sistem koordinat dan asalnya telah ditubuhkan, kami pergi ke persamaan. Magnitud yang menggambarkan pergerakan itu adalah:

-Halaju awal v_{Sama ada}

-Pecutan ke

-Kelajuan v

-Kedudukan awal x_{Sama ada}

-Kedudukan x

-Pemindahan Dx

-Masa t

Semua kecuali masa adalah vektor, tetapi kerana ia adalah pergerakan satu dimensi dengan arah tertentu, yang penting kemudian menggunakan tanda + atau - untuk menunjuk ke mana magnitud yang dipersoalkan. Dalam kes penembakan menegak, graviti selalu turun dan, melainkan dinyatakan sebaliknya, tanda diberikan -.

Terdapat persamaan yang disesuaikan untuk menembak menegak, menggantikan "x"Dengan"dan"Dan"ke"Dengan"g". Di samping itu, tanda (-) sepadan dengan graviti yang diarahkan:

1) Kedudukan: y = y_{Sama ada} + v_{Sama ada}.T - ½ g.t²

2) kelajuan: V = V_{Sama ada} - g.t

3) Kelajuan bergantung pada anjakan δdan: v² = v_{Sama ada}² - 2.g. Δdan

Contoh

Kemudian ada contoh permohonan untuk menembak menegak. Dalam resolusinya, berikut mesti diambil kira:

-"g"Ia mempunyai nilai malar yang rata -rata ialah 9.8 m/s² atau kira -kira 10 m/s² Sekiranya lebih disukai untuk memudahkan pengiraan apabila tidak terlalu tepat diperlukan.

-Bila v_{Sama ada} okey 0, Persamaan ini dikurangkan kepada orang -orang jatuh bebas.

-Sekiranya pelancaran selesai, objek perlu mempunyai kelajuan awal yang membolehkan anda bergerak. Sekali bergerak, objek mencapai ketinggian maksimum yang bergantung pada seberapa besar kelajuan awal. Sudah tentu lebih tinggi, mudah alih akan menghabiskan lebih banyak masa di udara.

-Objek kembali ke titik permulaan dengan kelajuan yang sama dengan yang dilancarkan, tetapi kelajuan ditujukan.

-Untuk pelancaran menegak ke bawah, semakin tinggi halaju awal, semakin cepat objek akan sampai ke tanah. Di sini jarak perjalanan ditetapkan mengikut ketinggian yang dipilih untuk pelancaran.

Boleh melayani anda: apa kekasaran relatif dan mutlak?

-Dalam tembakan menegak, masa yang mengambil mudah alih untuk mencapai ketinggian maksimum dikira dengan melakukan V = 0 Dalam persamaan 2) bahagian sebelumnya. Ini adalah masa maksimum t_Maks:

0 = v_{Sama ada} - g . t_Maks ⇒ t_Maks = v_{Sama ada} /g

-The ketinggian maksimum dan_Maks Ia dibersihkan dari persamaan 3) bahagian sebelumnya juga dilakukan V = 0:

0 = v_{Sama ada}² - 2.g. Δy ⇒ 0 = v_{Sama ada}² - 2.g. (dan_Maks - dan_{Sama ada}) ⇒ dan_Maks = y_{Sama ada}  + v_{Sama ada}² / 2 g

Yeah dan_{Sama ada} = 0, Ia dikurangkan menjadi:

dan_Maks = v_{Sama ada}² / 2 g

Diselesaikan Contoh 1

Bola dengan V dibuang ke atas secara menegak_{Sama ada} = 14 m/s, dari bahagian atas bangunan tinggi 18 m. Bola dibenarkan mengikuti hilirannya ke trotoar. Kira:

a) Ketinggian maksimum yang dicapai oleh bola berkenaan dengan tanah.

b) masa di udara (masa penerbangan).

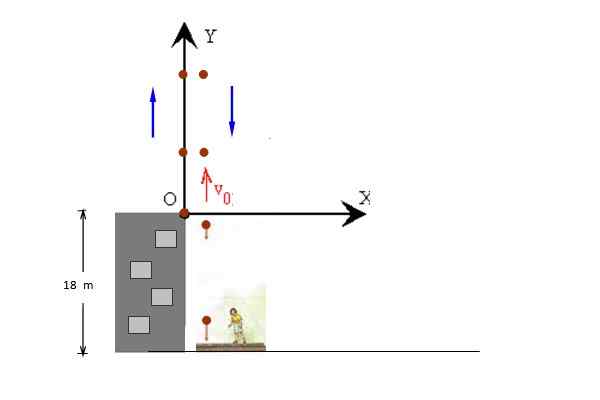Rajah 3. Bola dibuang secara menegak dari bumbung bangunan. Sumber: f. Zapata.

Penyelesaian

Dalam angka pergerakan kenaikan dan penurunan bola muncul secara berasingan untuk kejelasan, tetapi kedua -duanya berlaku di sepanjang garis yang sama. Kedudukan awal diambil pada y = 0, supaya kedudukan akhir adalah y = - 18 m.

a) Langkah maksimum yang diukur dari bumbung bangunan adalah dan_Maks = v_{Sama ada}² / 2 g Dan dari pernyataan itu dibaca bahawa kelajuan awal adalah +14 m/s, maka:

dan_Maks = (14 m/s)² / 2 x 9.8 m/s² = 10 m (Mengenai bumbung)

H_Maks = 10 m + 18 m = 28 m (Mengenai trotoar).

b) untuk mencari Jumlah masa Sama ada masa penerbangan Bertahan di udara bola akan digunakan persamaan y = y_{Sama ada} + v_{Sama ada}.T - ½ g.t², Dengan nilai dan tanda berikut:

y = - 18 m

dan_{Sama ada} = 0 m

v_{Sama ada} = +14 m/s

Mengganti:

- 18 = 14.T - ½ 9.8 .t²

- 4.9 t²+14.T + 18 = 0 

4.9 t²-14.T - 18 = 0

Ini adalah persamaan kedua yang mudah diselesaikan dengan bantuan kalkulator saintifik atau menggunakan resolusi. Penyelesaiannya adalah: 3.82 dan -0.96. Penyelesaian negatif dibuang kerana ia adalah masa yang tidak mempunyai makna fizikal.

Ia boleh melayani anda: Panas: Formula dan Unit, Ciri -ciri, Bagaimana Ia Diukur, Contohnya

Masa terbang bola adalah 3.82 saat.

Diselesaikan Contoh 2

Zarah yang dimuatkan positif dengan Q = +1.2 milicoulombs (mc) dan jisim M = 2.3 x 10 ^-10 Kg Ia diproyeksikan secara menegak, bermula dari kedudukan yang ditunjukkan dalam angka dan dengan kelajuan awal v_{Sama ada} = 30 km/s.

Antara plat yang dimuatkan terdapat medan elektrik Dan seragam, diarahkan secara menegak dan magnitud 780 N/C. Sekiranya jarak antara plat adalah 18 cm, adakah zarah akan bertembung dengan plat atas? Menghina tarikan graviti pada zarah, kerana ia sangat ringan.

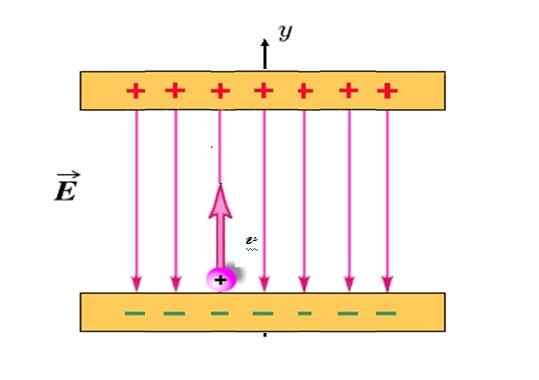Rajah 4. Zarah beban positif bergerak mirip dengan bola yang dilemparkan secara menegak ke atas, apabila ia direndam dalam medan elektrik angka. Sumber: diubahsuai oleh f. Wikimedia Commons Shoe.

Penyelesaian

Dalam masalah ini medan elektrik Dan adalah yang menghasilkan kekuatan F dan pecutan akibatnya. Dimuatkan secara positif, zarah sentiasa tertarik ke plat bawah, namun apabila ia diunjurkan secara menegak ke atas ia akan mencapai ketinggian maksimum dan kemudian kembali ke plat bawah, seperti bola dari contoh sebelumnya.

Dengan definisi medan elektrik:

E = f/q = m.A /Q ⇒ a = q.E / m

Adalah perlu menggunakan kesetaraan ini sebelum menggantikan nilai:

1 mc = 1 x 10^-3 C

Dengan ini pecutan adalah:

A = 1.2 x 10^-3 X 780/2.3 x 10 ^-10Cik² = 4.07 x 10⁹ Cik²

Untuk ketinggian maksimum formula bahagian sebelumnya digunakan, tetapi bukannya menggunakan "g"Nilai pecutan ini digunakan:

dan_Maks = v_{Sama ada}² / 2a = (30.000 m/s)²/2 x 4.07 x 10⁹ Cik² = 0.11 m = 11 cm

Jangan bertembung dengan plat atas, kerana ia adalah 18 cm dari titik permulaan, dan zarah sebaik sahaja ia menaikkan 11 cm.

https: // youuat.Be/kt08ntudzwq

Rujukan

1. Kirkpatrick, l. 2007. Fizik: Lihatlah dunia. 6^TA Edisi Singkat. Pembelajaran Cengage. 23 - 27.
2. Rex, a. 2011. Asas Fizik. Pearson. 33 - 36
3. Sears, Zemansky. 2016. Fizik universiti dengan fizik moden. 14^th. Ed. Jilid 1. 50 - 53.
4. Serway, r., Vulle, c. 2011. Asas Fizik. 9^na Ed. Pembelajaran Cengage. 43 - 55.
5. Wilson, J. 2011. Fizik 10. Pendidikan Pearson. 133 - 149.