Sifat transformasi linear, apakah penggunaan, jenis, contoh

A Transformasi linear, yang akan kita panggil, mengaitkan unsur -unsur dua ruang vektor V dan W, memberikan setiap vektor v milik v vektor tunggal W yang dimiliki oleh W, melalui operasi tertentu.

Transformasi ini memenuhi dua syarat:

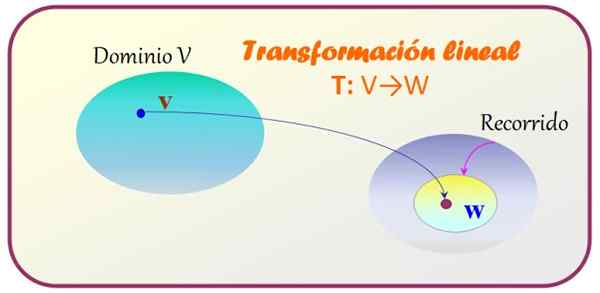
Rajah 1. Transformasi linear digunakan untuk vektor ruang vektor v untuk mendapatkan vektor lain milik ruang vektor w. Sumber: f. Zapata.

-Keadaan 1

Ia merujuk kepada penambahan, supaya transformasi t -linear perlu dipenuhi:

T (v + W) = T (v) + T (W)

-Keadaan 2

Keadaan kedua mewakili homogeniti dalam pendaraban skalar oleh vektor:

T (cv) = c ⋅T (v)

Transformasi linear, seperti namanya, bertanggungjawab untuk pemetaan atau mengubah unsur -unsur v ke dalam unsur -unsur w.

Notasi untuk fungsi juga digunakan dalam kes transformasi linear, oleh itu, domain v adalah set elemen (vektor) yang akan diubah, manakala codominium atau laluan adalah set yang dihasilkan.

Contoh transformasi linear ialah:

Untuk menunjukkan bahawa huruf t akan digunakan. Transformasi akan digunakan pada vektor v komponennya adalah x dan y, yang telah diwakili oleh matriks lajur tunggal. Hasilnya adalah vektor lain W komponennya adalah x dan 0, juga diwakili oleh matriks lajur.

Oleh itu, ini adalah transformasi ruang vektor r r r R² Ke arah ruang vektor r², Itu secara ringkasnya ditulis seperti ini:

T: r² → R²         

Sekiranya kita mempunyai vektor:

Transformasi mengembalikan kita:

Dan sebagainya dengan mana -mana vektor². Dalam Contoh 1, ia akan disahkan bahawa transformasi ini linear.

[TOC]

Sifat transformasi linear

Katakan transformasi linear V dalam W, di mana vektor v dan atau Mereka tergolong dalam V, maka sifat -sifat berikut dipenuhi:

Harta 1

T (0) = 0

Di mana 0 adalah vektor null.

Harta 2

T (-v) = - t (v)

Harta 3

T (atau  - v) = T (atau) - t (v)

Harta 4

Menjadi v = c₁v₁ + c₂v₂ +… . +  c_nv_n

 Jadi:

T (c₁v₁ + c₂v₂ +… . +  c_nv_n) = c₁ T (v₁) + c₂ T (v₂) +.. . +  c_n T (v_n)

Unsur transformasi linear

Biarkan V dan W sudah disebutkan ruang vektor di mana transformasi linear t mengubah unsur -unsur v hingga w. Kita boleh menentukan unsur -unsur berikut:

-C nukleus atau kernel: Ia adalah subset domain yang dilambangkan olehnya N (t) Sama ada Ker (T) dan memahami semua elemen v seperti itu:

T (v) = 0.

Transformasi linear t (v) = 0 dipanggil transformasi null.

Secara semulajadi vektor null v = 0 Memenuhi pula dengan keadaan ini, tetapi kernel terdiri daripada seluruh vektor non -null yang juga memenuhinya, untuk t yang diberikan.

Boleh melayani anda: Fungsi Berkembang: Cara Mengenalpasti, Contoh, Latihan

-Imej t: Ia adalah set vektor milik W yang merupakan imej sekurang -kurangnya beberapa vektor dalam v. Ia dilambangkan sebagai Im t) Dan ia adalah subset ruang vektor w.

Unsur -unsur ini akan membantu kita mengklasifikasikan transformasi linear kemudian.

Apakah transformasi linear untuk?

Pada mulanya, transformasi linear berfungsi dengan ruang vektor, dibentuk oleh vektor. Ramai kali kita mengaitkan vektor dengan kekuatan dan magnitud fizikal lain, namun dalam pemprosesan imej digital, piksel boleh diwakili oleh vektor.

Dalam hal ini, imej dapat dimanipulasi oleh transformasi linear yang mudah untuk mendapatkan kesan yang dikehendaki, contohnya memproyeksikan, berputar, mencari imej cermin atau mengubah saiznya tanpa mengubah dimensi relatif.

Transformasi linear juga digunakan secara meluas dalam ekonomi dan membuat keputusan, contohnya untuk mengetahui jumlah bahan mentah yang diperlukan untuk mengeluarkan kumpulan produk tertentu.

Bilangan kepingan yang diperlukan untuk memasang pelbagai model yang dihasilkan oleh sebuah kilang, dapat dikerjakan melalui susunan matriks, seperti yang akan kita lihat kemudian.

Jenis Transformasi Linear (Klasifikasi)

Seperti fungsi, transformasi linear boleh:

-Injective atau monomorfisme

-Bijak atau Epimorfisme

-Terlalu banyak atau Isomorfisme

Di samping itu adalah jenis berikut:

-Endomorphisms

-Automorphisms.

Transformasi linear injektif

Biarkan ruang v dan w vektor dan transformasi linear t: v → w. T adalah injak ketika:

Ker (T) = 0

Transformasi overjective linear

Jika V dan W adalah ruang vektor seperti T: V → W, dikatakan bahawa T adalah bijective apabila:

Im (t) = w

Transformasi linear Bijjective

Transformasi linear T: V → W adalah Bijektif apabila kedua -dua injak dan berlebihan. Oleh itu ia dipenuhi bahawa:

Ker (T) = 0 dan Im (t) = w

Endomorphisms

Mereka adalah transformasi linear di mana domain dan codominium bertepatan.

Automorphisms

Transformasi linear semacam ini adalah endomorfisme bijektif.

Transformasi linear khas

Pengendali linear

Transformasi linear T: V → V, yang keluar dari ruang vektor ke ruang vektor yang sama dipanggil Pengendali linear.

Transformasi sifar

Disebutkan di atas, transformasi sifar adalah penting untuk mencari kernel transformasi linear:

Ia dapat melayani anda: Tetradecágon

T: v → w seperti t (v) = 0 Bagi apa apa v.

Transformasi identiti

T: v → v seperti t (v) = v  Bagi apa apa v.

Transformasi yang ditakrifkan oleh matriks

T: v → w seperti t (v) = Av, di mana A adalah matriks dan v Ia adalah vektor lajur.

Funtion lineal

Fungsi linear jenis y = mx adalah transformasi linear. Ambil contoh y = 3x dan lihat apakah ia memenuhi dua syarat permulaan, menguji dengan dua nilai a dan b mana -mana:

F (a+b) = 3 (a+b) = 3a+3b = f (a)+f (b)

f (ka) = 3 (ka) = k ⋅ (3a) = k ⋅F (a)

Memang ia adalah transformasi linear.

Aplikasi

Transformasi linear mempunyai aplikasi matematik, seperti:

-Menyelaras putaran gandar.

-Dalam penyelesaian sistem persamaan pembezaan linear.

-Masalah nilai diri dan autovery.

Dan mereka juga mempunyai aplikasi dalam bidang sains lain, contohnya dalam mekanik, mekanik kuantum dan ekonomi, antara lain.

Contoh transformasi linear

Contoh 1

Dalam banyak masalah mekanik kita perlu mencari unjuran vektor v milik ruang, di atas kapal terbang tertentu. Vektor ini v boleh mewakili contoh kekuatan.

Katakan anda mahu memproyeksikan vektor v = Pada satah xy. Kita boleh menentukan transformasi linear yang diberikan oleh matriks berikut:

Apabila kita memohon kepada vektor v Kami mendapat vektor yang komponen Z dibatalkan. Secara geometri ia diwakili, dengan unjuran v Di pesawat XY sebagai vektor merah dengan dua komponen.

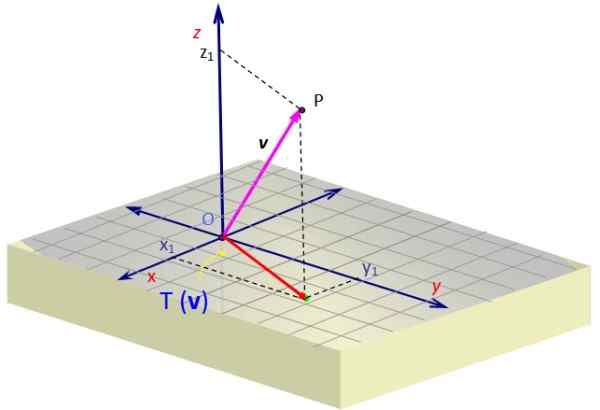Rajah 2. Unjuran vektor di ruang angkasa, yang diperoleh melalui transformasi linear. Sumber: f. Zapata.

Contoh 2

Katakan anda mempunyai kilang yang menghasilkan tiga jenis kereta mainan: C1, C2 dan C3, yang mana anda pada gilirannya memerlukan tiga jenis kepingan dalam kuantiti tertentu untuk mengeluarkan setiap jenis kereta:

-Paksi atau sekeping

-Roda atau sekeping b

-Casis atau sekeping c

Untuk setiap jenis kereta, bilangan kepingan berbeza, kerana model berbeza. Kami dapat menampung jumlah dalam matriks 3 × 3, di mana lajur diketuai oleh jenis kereta, dan pangkatnya sesuai dengan jumlah kepingan yang diperlukan untuk menghuraikan setiap model.

Ini adalah contoh transformasi yang diberikan oleh matriks yang akan menjadi seperti ini:

Sekiranya kilang menerima pesanan pembelian tertentu, yang terdiri daripada x Jumlah C1, dan  C2 dan z Dari C3, berapa keping A, B dan C perlu disediakan untuk memasang gerai pesanan?

Ia dapat melayani anda: apakah ungkapan algebra dan yang paling kerap?

Kita mesti mencari transformasi linear t (x) seperti itu:

Untuk mendapatkan vektor dan:

Yang akan memberi kita jumlah bahagian yang mesti kita ada. Pada tahun yang diselesaikan 2 kita menilai keberkesanan transformasi linear untuk mencari jumlah bahagian yang diperlukan untuk memenuhi pesanan tertentu.

Latihan yang diselesaikan

- Latihan 1

Periksa bahawa transformasi berikut T: r² → R² Ia linear:

Penyelesaian

Untuk melakukan ini, anda mesti memastikan bahawa transformasi memenuhi kedua -dua syarat yang diterangkan pada mulanya, pertama penambahan dan kemudian produk skalar untuk vektor. Oleh itu, anda mesti mengambil dua vektor v dan  atau kepunyaan r², menulisnya dengan notasi matriks atau menentukan komponen.

Vektor ini adalah:

v = x₁, dan₁

atau = x₂, dan₂

Keadaan pertama

-Ingat bahawa vektor ditambah komponen komponen, ia mesti disahkan bahawa:

T (v+atau) = T (v) + T (atau)

T (v+atau) = T (x₁+ x₂ ; dan₁ + dan₂)

Dari sini diperolehi:

T (x₁+ x₂ ; dan₁ + dan₂) = (x₁+ x₂; 0)

-Sebaliknya, apabila menggunakan transformasi kepada setiap vektor secara berasingan:

T (x₁,dan₁) + T (x₂,dan₂) = (x₁,0) + (x₂,0)

Dengan menambahkan vektor yang dihasilkan, ia diperoleh dengan berkesan:

W = (X₁+ x₂; 0)

Oleh kerana kedua -dua keputusan adalah sama, keadaan pertama berpuas hati.

Keadaan kedua

Sekarang kita akan mengesahkan bahawa dengan mendarab dengan scler c, ia boleh keluar dari transformasi:

T (cv) = c ⋅T (v)

Sean:

v = x₁, dan₁

c.v = C ⋅x₁, C ⋅Y₁

Jadi:

T (cv) = T (c ⋅x₁, C ⋅y₁ ) = (C ⋅x₁ , 0)

Tetapi kita tahu bahawa dari langkah sebelumnya T (T (v) = T (x₁, dan₁ ) = (X₁ , 0).

Oleh kerana kedua -dua ungkapan adalah sama, keadaan kedua juga dipenuhi dan transformasi adalah linear.

- Latihan 2

Kilang kereta mainan memasang tiga model kenderaan: C1, C2 dan C3, yang mana anda memerlukan kepingan A, B dan C yang masing -masing gandar, roda dan casis. Jumlah yang diperlukan adalah dalam jadual berikut:

Kilang telah diminta menyediakan 12 model C1, 22 C2 dan 16 C3. Berapa banyak keping A, B dan C diperlukan untuk menyelesaikan pesanan?

Penyelesaian

Transformasi linear t (x) = y digunakan, yang hasilnya adalah produk antara matriks:

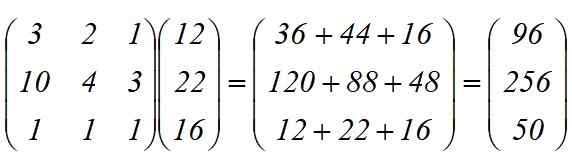
Mereka diperlukan secara total:

-96 paksi

-256 roda

-50 casis.

Rujukan

1. Algebra dan geometri analisis. Teras dan imej. Klasifikasi transformasi linear. Pulih dari: aga.frba.Utn.Edu.ar.
2. Grossman, s. 2012. Algebra linear. Ke -7. Edisi. McGraw Hill.
3. Gutiérrez, e. 2014. Algebra linear dan aplikasinya. Kumpulan Editorial Patria.
4. Larson, r. 2016. Asas aljabar linear. 6th. Edisi. Pembelajaran Cengage.
5. Wikipedia. Aplikasi linear. Pulih dari: Adakah.Wikipedia.org.