Vektor unit ciri, bagaimana untuk mengeluarkannya, contohnya

The vektor unit adalah mereka yang modul, magnitud atau saiznya sama dengan nilai berangka satu. Vektor unit berguna untuk menunjukkan arah vektor bukan lain.

Ingatlah bahawa vektor adalah entiti matematik yang secara matematik mewakili magnitud fizikal yang bergantung kepada arah, seperti kekuatan, kelajuan, pecutan dan lain -lain.

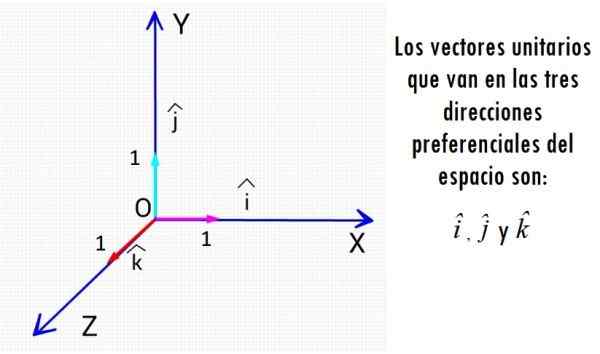
Vektor unit yang paling terkenal adalah tiga vektor yang pergi ke arah paksi Cartesian. Sumber: f. Zapata.

Tidak kira magnitud fizikal yang dikaitkan, vektor unit adalah entiti yang kurang unit ukuran dan saiznya selalu 1, nombor murni.

Sebagai contoh, kelajuan zarah yang bergerak pada 3 m/s dan masuk ke arah positif paksi X Cartesian dilambangkan: v = (3 m/s) Yo, di mana huruf berani digunakan untuk menandakan jumlah vektor. Dalam contoh ini modul v Ia adalah 3 m/s dan modul vektor unit Yo adalah 1 (tanpa unit).

[TOC]

Modul, arah dan makna

Diberikan yang penting. Pada masa mewakili jumlah vektor, perlu dengan jelas menunjukkan aspek -aspek ini.

Sekarang, vektor unit boleh mempunyai arahan dan makna yang lebih disukai, tetapi magnitud mestilah sama dengan 1.

Vektor unit digunakan untuk menunjukkan alamat peribadi di ruang angkasa atau dalam pesawat. Jika, sebagai contoh, kita perlu bekerja dengan semua daya yang bertindak di sepanjang paksi mendatar, kerana vektor unit ke arah itu membantu kita membezakan daya ini dari orang lain yang diarahkan ke arah yang berbeza.

Dan untuk membezakannya dari vektor bukan -unit, berani biasanya digunakan dalam cetakan dan meletakkan aksen circumflex di atas, sebagai contoh:

Ia boleh melayani anda: Teori Negeri pegun: Sejarah, Penjelasan, Berita

Untuk lirik tulisan tangan, sudah cukup untuk meletakkan circumflejo untuk memahami bahawa ia adalah vektor unit.

Ciri -ciri vektor unit

Secara matematik vektor unit:

Ia adalah elemen yang dimiliki oleh ruang vektor ℛ dimensi n, sehingga |v| = 1, di mana bar bermaksud "modul".

Oleh itu, kita dapat menetapkannya:

-Modul vektor kesatuan selalu 1, tidak kira sama ada kekuatan, kelajuan atau vektor lain.

-Vektor unit mempunyai arah tertentu, serta arah, seperti vektor unit dalam arah menegak, yang mungkin masuk atau turun.

-Vektor unit mempunyai titik asal. Apabila diwakili oleh sistem koordinat Cartesian, titik tersebut bertepatan dengan asal sistem: (0.0) jika ia adalah satah atau (0.0.0) jika vektor berada dalam ruang tiga dimensi.

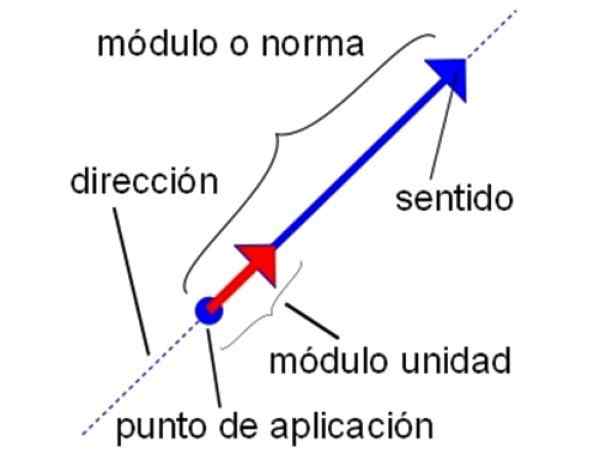Ciri -ciri vektor unit. Sumber: Wikimedia Commons.

-Juga dengan vektor unit, semua operasi jumlah, penolakan dan pendaraban vektor yang dibuat oleh vektor biasa boleh dilakukan. Oleh itu, sah untuk membiak vektor unit dengan skalar, serta menjalankan produk titik dan produk silang.

-Dengan vektor unit ke arah tertentu, vektor lain juga boleh dinyatakan yang juga berorientasikan ke arah itu.

Vektor unit di ruang angkasa

Untuk menyatakan mana -mana vektor di ruang angkasa atau dalam satah, anda boleh menggunakan satu set vektor kesatuan yang berserenjang antara satu sama lain, yang membentuk asas ortonormal. Setiap satu daripada tiga arah keutamaan ruang mempunyai vektor unit sendiri.

Mari kembali kepada contoh kekuatan yang diarahkan sepanjang paksi mendatar. Ini adalah paksi x, yang mempunyai dua kemungkinan: arah ke kanan dan arah ke kiri. Katakan terdapat vektor unit pada paksi x dan diarahkan ke kanan, yang boleh kita nyatakan melalui mana -mana bentuk ini:

Boleh melayani anda: model atom Thomson: ciri -ciri, postulates, zarah subatomik

Mana -mana daripada mereka sah. Sekarang, anggap kekuatan F₁ magnitud 5 n di sepanjang paksi ini dan diarahkan ke kanan, daya sedemikian boleh dinyatakan sebagai:

Sekiranya daya diarahkan sepanjang paksi x tetapi ke arah yang bertentangan, iaitu, ke kiri, maka tanda negatif boleh digunakan untuk menetapkan perbezaan ini.

Sebagai contoh, kekuatan 8 n magnitud, yang terletak di paksi x dan diarahkan ke kiri akan menjadi seperti ini:

Atau lebih:

Dan untuk vektor yang tidak diarahkan di sepanjang paksi Cartesian, terdapat juga cara untuk mewakili mereka dari segi vektor unit ortogonal, melalui komponen Cartesian mereka.

Cara mengeluarkan/mengira vektor unit?

Untuk mengira vektor unit ke arah mana -mana vektor sewenang -wenang v, Formula berikut digunakan:

Di mana:

Ia adalah modul atau magnitud vektor v, yang persegi dikira seperti ini:

|v|² = (v_x)² +  (v_dan)²+  (v_z)²

Vektor sewenang -wenang dari segi vektor unit

Sebagai alternatif vektor v Ia boleh dinyatakan seperti berikut:

Iaitu, produk modulnya oleh vektor unit yang sepadan. Inilah yang telah dilakukan sebelum ini, ketika bercakap tentang kekuatan 5 n magnitud yang diarahkan sepanjang paksi x positif.

Perwakilan grafik

Secara grafik, apa yang dikatakan dilihat dalam imej ini, di mana vektor v Ia berwarna biru dan vektor unit yang sepadan ke arahnya berwarna merah.

Dalam contoh ini, vektor v Ia mempunyai magnitud yang lebih besar daripada vektor unit, tetapi penjelasannya bahkan sah jika ini tidak berlaku. Dengan kata lain, kita boleh mempunyai vektor yang contohnya 0.25 kali vektor unit.

Boleh melayani anda: Berat (fizikal): pengiraan, unit, contoh, latihan

Contoh vektor unit

Vektor unit tegak lurus i, j dan k

Seperti yang telah kita lihat sebelumnya, vektor unit tegak lurus Yo, J dan k Mereka sangat berguna untuk mewakili mana -mana vektor lain dalam pesawat atau ruang, dan menjalankan operasi vektor. Dari segi vektor tersebut, vektor sewenang -wenang V diwakili sebagai:

v = v_x Yo + v_dan J + v_z k

Di mana v_x, v_dan dan v_z adalah komponen segi empat tepat vektor v, yang mendaki -bold tidak digunakan untuk mewakili mereka dalam teks bercetak-.

Undang -undang Coulomb

Vektor kesatuan sering muncul dalam fizik. Di sana kita mempunyai undang -undang Coulomb, sebagai contoh, yang secara kuantitatif menggambarkan interaksi antara dua caj elektrik tertentu.

Ia menunjukkan bahawa daya F daya tarikan atau penolakan antara beban ini adalah berkadar dengan produk mereka, berkadar songsang dengan kuadrat jarak yang memisahkannya dan diarahkan ke arah vektor unit yang bergabung dengan beban.

Vektor ini biasanya diwakili oleh:

Dan undang -undang Coulomb adalah seperti ini, dalam bentuk vektor:

Di mana k Ia adalah pemalar elektrostatik, q₁ dan q₂ Mereka adalah beban dan r Ia adalah jarak yang memisahkan mereka.

Latihan diselesaikan

Cari vektor unit ke arah vektor v = 5Yo + 4J -8k, Diberikan dalam unit sewenang -wenang.

Penyelesaian

Takrif vektor kesatuan di atas digunakan di atas:

Tetapi pertama -tama anda perlu mengira modul vektor, yang mempunyai tiga komponen, ditentukan oleh:

|v|² = (v_x)² +  (v_dan)² +  (v_z)²

Menginap:

|v|² = (5)² +  (4)² +  (-8)²= 25 + 16 + 64 = 105

Oleh itu modul v adalah:

|v| = √105

Vektor kesatuan dicari adalah semata -mata:

Yang akhirnya membawa kita ke:

v = 0.488 Yo + 0.390 J - 0.781 k

Rujukan

1. Bauer, w. 2011. Fizik untuk Kejuruteraan dan Sains. Jilid 1. MC Graw Hill.
2. Bedford, 2000. Ke. Mekanik untuk Kejuruteraan: Statik. Addison Wesley.
3. Figueroa, d. (2005). Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 1. Kinematik. Diedit oleh Douglas Figueroa (USB).
4. GiMbattista, a. 2010. Fizik. 2. Ed. McGraw Hill.
5. Resnick, r. (1999). Fizikal. Vol. 1. Edisi ke -3. dalam bahasa Sepanyol. Syarikat Editorial Continental s.Ke. daripada c.V.