X Squared

Kami menerangkan apa yang X Squared, sifat, contoh dan latihannya diselesaikan

Kawasan kuadrat "x" adalah x kuadrat. Sumber: f. Zapata.

Operasi algebra "X Squared"Ia dijalankan dengan mengalikan jumlah" x "dengan sendirinya dua kali. Ia adalah sebahagian daripada operasi potentiasi, dan dalam simbol matematik, ia dinyatakan dengan cara ini:

x ∙ x = x²

Ini adalah kes pemberdayaan tertentu, di mana "x" mewakili asas Dan "2" adalah eksponen. Sekiranya dalam operasi istilah x muncul², Ia dibaca dengan tepat sebagai "x kuadrat" atau "x persegi dinaikkan".

Sememangnya, eksponen lain mungkin, sebagai contoh, jika eksponen adalah 3, maka kuasa ditulis sebagai:

x ∙ x ∙ x = x³

Dan baca sebagai "x ke tiga", "X dibesarkan ke kiub" atau hanya "x ke kiub".

Secara umum, eksponen yang asasnya tinggi boleh menjadi nombor, yang dipanggil "n" dan dalam kes itu, kuasa yang sama ditulis:

xⁿ = x ∙ x ∙ x ∙ ... ∙ x

Di sini titik -titik yang menggalakkan menunjukkan bahawa "x" mesti didarab dengan sendirinya "n", iaitu, seberapa banyak kali eksponen menunjukkannya.

Beberapa contoh mudah "X Squared", dengan nombor, adalah yang berikut:

3² = 3 ∙ 3 = 9

(-4)² = (-4) ∙ (-4) = 16

Kemudian, pelbagai aplikasi diterangkan yang perlu.

Sifat potentiasi

Secara umum, produk dari apa -apa jumlah dengan sendirinya, n kali, ia dipanggil potentiation. Pengiraan X Squared hanya satu kes tertentu potentiation, dua kes lain muncul apabila anda ingin menaikkan jumlah kepada eksponen 1, memperoleh hasil yang sama:

Boleh melayani anda: Undang -undang eksponen

Oleh kerana operasi ini kerap, untuk bekerja dengan pangkalan dan eksponen, beberapa peraturan operasi mudah diikuti, dipanggil Undang -undang eksponen, yang disenaraikan di bawah:

Undang -undang eksponen

Dalam apa yang berikut, "x" adalah asas dan "n" dan "m" adalah eksponen.

1.- Produk kuasa asas yang sama

Dengan mengalikan dua (atau lebih) kuasa asas yang sama, asasnya dinaikkan kepada jumlah eksponen diperoleh:

xⁿ∙ x^m = x^n+m

Dalam kes x tinggi, peraturan ini digunakan seperti berikut, menggantikan n dan m untuk 1:

x¹∙ x¹ = x¹⁺¹ = x²

2.- Bahagian Kuasa Pangkalan Sama Sama

Dengan membahagikan kuasa asas yang sama, asasnya diperoleh, dibangkitkan kepada penolakan antara eksponen pengangka dan penyebut:

xⁿ ÷ x^m = x^N-m

Oleh kerana pembahagian oleh 0 tidak ditakrifkan, ia mesti dipenuhi dengan syarat bahawa x ≠ 0.

3.- Kuasa Kekuatan

Hasil kuasa kuasa adalah sama dengan asas yang ditinggikan dengan produk eksponen:

(x^m)ⁿ = x^m∙n

Ia boleh diperoleh lagi x persegi, ketika melakukan m = 1 dan n = 2:

(x¹)² = x^1∙2 = x²

4.- Eksponen negatif

Untuk eksponen negatif, operasi yang akan dilakukan adalah:

Setiap kali x ≠ 0. Perhatikan bahawa, dalam kes ini, kuasa menjadi pecahan dengan pengangka yang sama dengan 1.

5.- Eksponen pecahan

Eksponen pecahan boleh ditulis sebagai akar nth asas:

Dengan syarat bahawa n berbeza dari 0. Nilai ini menjadi indeks akar, manakala m menjadi eksponen kuantiti di bawah akar, yang dalam kes ini adalah x.

Boleh melayani anda: apakah panduannya? (Geometri)

Produk dan kuota pangkalan yang berbeza

Apabila anda perlu meningkatkan produk dan quotients asas "x" dan "y" yang berbeza, peraturan ini diikuti:

1.- Kuasa produk

Untuk melaksanakan kuasa ini, setiap amaun dinaikkan kepada eksponen n dan produk yang dihasilkan ditubuhkan:

(x ∙ y)ⁿ = xⁿ ⋅ danⁿ

2.- Nisbah Kota

Sekali lagi, setiap jumlah mesti dibangkitkan kepada eksponen n secara berasingan dan menubuhkan kuota yang hasilnya, mengikuti peraturan bahawa jumlah "y" adalah berbeza dari 0, dalam hal positif "n":

(x ÷ y)ⁿ = xⁿ ÷ yⁿ

Apabila "n" adalah negatif, berhati -hati mesti diambil, kerana harta 4 bahagian sebelumnya, pengangka menjadi penyebut. Dalam kes ini, kedua -dua jumlahnya harus berbeza dari 0, kerana pembahagian oleh 0 harus dielakkan di semua kos.

Contoh

Contoh 1: Squares of Natural Number

Kuadrat sepuluh nombor semulajadi adalah:

• 1²= 1 × 1 = 1
• 2²= 2 × 2 = 4
• 3²= 3 × 3 = 9
• 4²= 4 × 4 = 16
• 5²= 5 × 5 = 25
• 6²= 6 × 6 = 36
• 7²= 7 × 7 = 49
• 8²= 8 × 8 = 64
• 9²= 9 × 9 = 81
• 10²= 10 × 10 = 100

Contoh 2: kuadrat nombor negatif

Bekas nombor negatif sentiasa positif, kerana dua jumlah tanda yang sama didarabkan, oleh itu:

(-x) · (-x) = x ∙ x = x²

Sebagai contoh:

(-2) · (-2) = (-2)² = 4

Contoh 3: persegi jumlah dan perbezaan

Selalunya perlu untuk mengira kuadrat jumlah dua kuantiti, atau perbezaannya, operasi yang dimasukkan ke dalam kategori produk terkenal.

Operasi ini diselesaikan dengan petunjuk yang diberikan dan bantuan harta pengedaran:

Persegi jumlah

Biarkan dua "x" dan "y" jumlah, dan anda ingin mencari kuadrat jumlahnya (x + y)²:

Boleh melayani anda: hierarki operasi

(x + y)² = (x + y) ∙ (x + y) = x ∙ x + x ∙ y + y ∙ x + y ∙ y = x² + 2x ∙ y + dan²

Ungkapan ini berbunyi seperti ini: "persegi yang pertama, ditambah dengan produk ganda yang pertama untuk yang kedua ditambah persegi yang kedua".

Persegi perbezaan

Ia diselesaikan secara analog, tetapi dengan mengambil kira tanda negatif:

(x - y)² = (x - y) ∙ (x - y) = x ∙ x - x ∙ y + y ∙ x - y ∙ y = x² - 2x ∙ dan + dan²

Contoh 4: Kawasan persegi

Dataran adalah poligon 4 -sided, yang mempunyai ukuran yang sama. Biarkan ℓ menjadi pengukuran sampingan, maka kawasan A dari angka diberikan oleh:

A = ℓ²

Contoh 5: Teorem Pythagoras

Teorem ini digunakan untuk segitiga segi empat tepat, yang mana dua bahagiannya membentuk sudut lurus. Sisi ini dikenali sebagai "kategori" dan bahagian yang tinggal adalah "hipotenus".

Teorem menetapkan bahawa kuadrat hypotenusa sama dengan jumlah kuadrat kategori. Memanggil "a" dan "b" kepada kategori, dan "c" kepada hipotenus, teorem ditulis sebagai:

c² = a² + b²

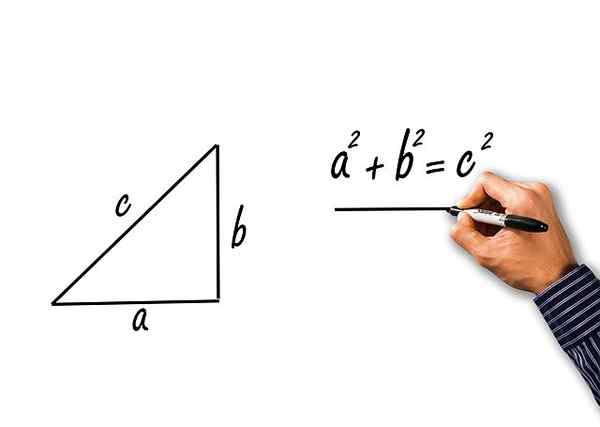Teorem Pythagoras untuk segitiga segi empat tepat kucing a dan b, dan hypotenusa c

Latihan yang diselesaikan

Latihan 1

Kirakan kuadrat hipotenus yang kaki mengukur 3 dan 5 unit.

Penyelesaian

Menurut teorem Pythagoras, persegi hipotenus adalah:

c² = a² + b²

Menggantikan nilai:

c² = 3² + 5²= (3 × 3) + (5 × 5) = 9 + 25 = 34

Latihan 2

Tentukan kawasan persegi sisi ℓ = 6 cm

Penyelesaian

A = ℓ² = (6 cm)² = 36 cm²