Konsep analisis mesh, kaedah, contoh

Dia Analisis mesh Ia adalah teknik yang digunakan untuk menyelesaikan litar elektrik rata. Prosedur ini juga boleh muncul dalam kesusasteraan dengan nama kaedah arus litar o Kaedah Arus mesh (atau gelung).

Asas kaedah analisis litar elektrik ini dan lain -lain adalah undang -undang Kirchhoff dan Undang -undang Ohm. Undang -undang Kirchhoff pada gilirannya, adalah ungkapan dua prinsip pemuliharaan yang sangat penting dalam fizik untuk sistem terpencil: kedua -dua caj elektrik dan tenaga dipelihara.

Rajah 1. Litar adalah sebahagian daripada peranti yang tidak terhitung jumlahnya. Sumber: Pixabay.

Di satu pihak, caj elektrik berkaitan dengan arus, yang bergerak beban, sementara dalam litar tenaga dikaitkan dengan voltan, yang merupakan ejen yang bertanggungjawab untuk melakukan kerja yang diperlukan untuk memastikan beban bergerak.

Undang -undang ini, yang digunakan untuk litar rata, menghasilkan satu set persamaan serentak yang mesti diselesaikan untuk mendapatkan nilai semasa atau voltan.

Sistem persamaan dapat diselesaikan dengan teknik analisis yang sudah diketahui, seperti Peraturan Cramer, yang memerlukan pengiraan penentu untuk mendapatkan penyelesaian sistem.

Bergantung pada bilangan persamaan, mereka diselesaikan menggunakan kalkulator saintifik atau perisian matematik. Di rangkaian terdapat juga banyak pilihan yang ada.

[TOC]

Istilah penting

Sebelum menjelaskan bagaimana ia berfungsi, kita akan bermula dengan menentukan istilah ini:

Cawangan: Seksyen yang mengandungi elemen litar.

Nod: titik yang menghubungkan dua atau lebih cawangan.

Riben: Ia adalah bahagian tertutup litar, yang bermula dan berakhir dengan nod yang sama.

Mesh: gelung yang tidak mengandungi sebarang ikatan lain di dalamnya (Mesh penting).

Kaedah

Analisis messeal adalah kaedah umum yang berfungsi untuk menyelesaikan litar yang unsur -unsurnya disambungkan secara siri, selari atau bercampur, iaitu, apabila jenis sambungan tidak dibezakan dengan jelas. Litar mestilah rata, atau sekurang -kurangnya mungkin untuk membayarnya.

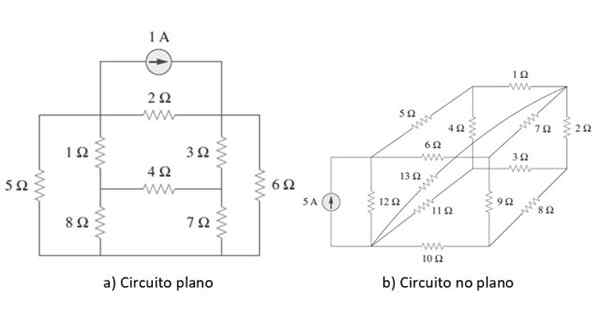Rajah 2. Litar rata dan bukan -flat. Sumber: Alexander, C. 2006. Asas Litar Elektrik. Ke -3. Edisi. MC Graw Hill.

Contoh setiap jenis litar ditunjukkan dalam angka di atas. Sebaik sahaja titik itu dijelaskan, bermula, kami akan menggunakan kaedah ini ke litar mudah sebagai contoh di bahagian seterusnya, tetapi sebelum kita mengkaji secara ringkas undang -undang Ohm dan Kirchhoff.

Undang -undang ohm: Sean V Voltan, R rintangan e Yo Arus unsur rintangan ohmik, di mana voltan dan arus berkadar terus, rintangan menjadi pemalar berkadar:

Boleh melayani anda: graviti API: skala dan klasifikasi minyak mentah

V = i.R

Undang -undang Kirchhoff Voltan (LKV): Dalam mana -mana trajektori tertutup yang dilalui dalam satu arah, jumlah algebra voltan adalah sifar. Ini termasuk voltan kerana sumber, perintang, induktor atau kapasitor: Σ e = Σ r_Yo. Yo

Kirchhoff semasa (LKC): Di mana -mana nod, jumlah algebra arus adalah sifar, dengan mengambil kira bahawa arus yang masuk diberikan tanda dan yang lain keluar. Dengan cara ini: Σ i = 0.

Dengan kaedah arus mesh, tidak perlu.

- Langkah -langkah untuk menggunakan analisis mesh

Kami akan mula menerangkan kaedah untuk litar 2 meshes. Prosedur ini boleh dilanjutkan kemudian untuk litar yang lebih besar.

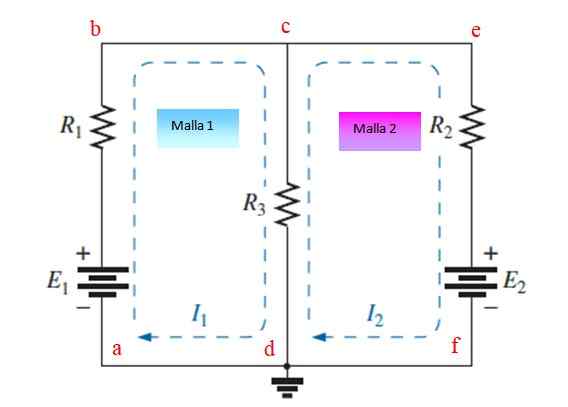Rajah 3. Litar dengan rintangan dan sumber yang diatur dalam dua jejaring. Sumber: f. Zapata.

Langkah 1

Berikan dan lukis arus bebas untuk setiap mesh, dalam contoh ini Yo₁ dan Yo₂. Mereka boleh ditarik dalam jadual atau juga anti -horary.

Langkah 2

Sapukan undang -undang ketegangan kirchhoff (LTK) dan undang -undang ohm untuk setiap mesh. Potensi jatuh diberikan tanda (-) sementara kenaikan diberikan tanda (+).

Abcda mesh

Bermula dari titik A dan mengikuti makna arus, kita dapati kenaikan potensi dalam bateri e1 (+), kemudian kejatuhan r dalam r₁ (-) dan kemudian jatuh lagi dalam r₃ (-).

Pada masa yang sama, rintangan r r₃ Ia juga diseberang oleh semasa i₂, Tetapi ke arah yang bertentangan, oleh itu ia mewakili kenaikan (+). Persamaan pertama adalah seperti ini:

Dan₁-R₁.Yo₁ -R₃.Yo₁ + R₃.Yo₂ = 0

Segera pemfaktoran dan istilah -istilah yang mempromosikan:

- (R₁+R₃) Yo₁ +R₃Yo₂ = -E₁  (Persamaan 1)

CEFDC mesh 

Bermula dari titik dan dan mengikuti makna arus adalah penurunan potensial R₂ (-), yang lain jatuh Dan₂, Oleh kerana arus memasuki tiang bateri + dan akhirnya jatuh lagi R₃ (-), pada masa yang sama semasa Yo₁ Ia melintasi R₃ Ke arah yang bertentangan (+).

Persamaan kedua, dengan tanda -tanda yang ditunjukkan, tetap dengan cara ini:

- R₂ Yo₂ - Dan₂ -R₃ Yo₂ +R₃ Yo₁= 0

R₃Yo₁ - (R₂ +R₃₎ Yo₂ = E₂  (Persamaan 2)

Perhatikan bahawa terdapat dua persamaan dengan dua yang tidak diketahui dan₁ dan saya₂.

Langkah 3

Maka sistem persamaan yang terbentuk diselesaikan.

Latihan yang diselesaikan

Untuk memulakan, adalah penting untuk mengambil kira perkara berikut:

-Arus ikatan atau mesh dapat diberikan arah sewenang -wenang.

-Kepada setiap mesh penting - atau "tetingkap" - bahawa litar mesti diberikan arus.

Boleh melayani anda: proses isocoric

-Arus mesh dipanggil dengan huruf modal untuk membezakannya dari arus yang beredar di cawangan, walaupun dalam beberapa kes arus yang beredar melalui cawangan boleh sama dengan mesh.

- Contoh 1

Cari arus yang beredar melalui setiap rintangan dalam litar dalam Rajah 3, jika elemen mempunyai nilai berikut:

R₁ = 20 Ω; R₂ = 30 Ω; R₃ = 10 Ω; Dan₁ = 12 V; Dan₂ = 18 v

Penyelesaian

Di tempat pertama adalah perlu untuk memberikan arus mesh dan₁ dan saya₂ dan ambil sistem persamaan seperti yang disimpulkan dalam bahagian sebelumnya, kemudian gantikan nilai yang diberikan dalam pernyataan:

- (R₁+R₃) Yo₁ +R₃Yo₂ = -E₁  (Persamaan 1)

R₃Yo₁ - (R₂ +R₃₎ Yo₂ = E₂     (Persamaan 2)

-

-(20+30) Yo₁ + 10i₂ = -12

10i₁ - (30 +10) i₂ = 18      

--

-lima puluhYo₁ + 10i₂ = -12

10i₁ - 40 i₂ = 18      

Kerana ia adalah sistem persamaan 2 x 2, ia dapat dengan mudah diselesaikan dengan pengurangan, mendarabkan dengan 5 persamaan kedua untuk menghapuskan yang tidak diketahui Yo₁:

-lima puluhYo₁ + 10 i₂ = -12

50i₁ - 200 i₂ = 90

-     

-190 i₂= 78

Yo₂ = - 78/180 a = - 0.41 a

Arus segera dibersihkan Yo₁ mana -mana persamaan asal:

Yo₁ = (18 + 40 i₂) / 10 = (18 + 40 x (-0.41)) / 10 = 0.16 a

Tanda negatif semasa semasa Yo₂ bermaksud bahawa arus dalam 2 mesh beredar bertentangan dengan lukisan.

Arus dalam setiap rintangan adalah seperti berikut:

Untuk rintangan R₁ Semasa beredar Yo₁ = 0.16 a dalam erti kata yang ditarik, dengan perlawanan R₂ Semasa beredar Yo₂ = 0.41 a bertentangan dengan yang ditarik, dan untuk rintangan R₃ beredar Yo₃ = 0.16- (-0.41) a = 0.57 a ke bawah.

Penyelesaian sistem dengan kaedah Cramer

Dalam cara matriks, sistem dapat diselesaikan seperti berikut:

Langkah 1: Kirakan δ

 Penting: Apabila δ = 0, sistem tidak mempunyai penyelesaian, ia adalah sistem yang tidak serasi.

Langkah 2: Kirakan δ₁

Lajur pertama digantikan oleh terma bebas sistem persamaan, mengekalkan urutan di mana sistem itu pada asalnya dibangkitkan:

Langkah 3: Kirakan i₁

Yo₁ = Δ₁/Δ = 300/1900 = 0.16 a

Langkah 4: Kirakan δ₂

 Langkah 5: Kirakan i₂

Yo₂ = Δ₂/Δ = -780/1900 = -0.41 a

- Contoh 2

Tentukan arus dan voltan melalui setiap rintangan dalam litar berikut, melalui kaedah arus mesh:

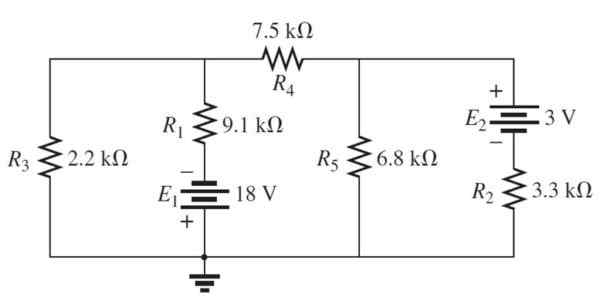Rajah 4. 3 litar mesh. Sumber: Boylestad, r. 2011. Pengenalan kepada Analisis Litar.2. Edisi. Pearson.

Penyelesaian

Tiga arus mesh ditarik, seperti yang ditunjukkan dalam angka berikut, dalam deria sewenang -wenang. Sekarang jejaring berjalan dari mana saja:

Ia boleh melayani anda: Imantation: Apa yang terdiri, kaedah dan contoh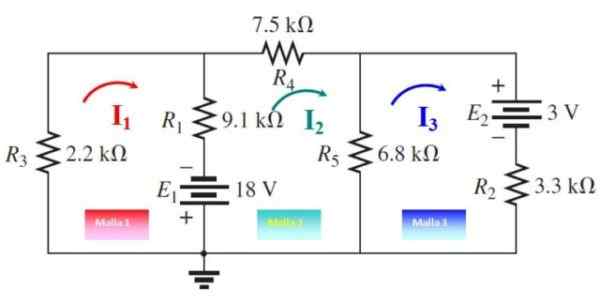 Rajah 5. Arus mesh untuk latihan 2. Sumber: f. Zapata, diubahsuai dari Boylestad.

Mesh 1

-9100.Yo₁+18-2200.Yo₁+9100.Yo₂= 0

-11300 i₁ + 9100.Yo₂ = -18

Mesh 2       

-(7500 +6800 +9100) .Yo₂ + 9100.Yo₁+6800.Yo₃-18 = 0

9100.Yo₁ - 23400.Yo₂ + 6800.Yo₃ = 18

Mesh 3  

-(6800 + 3300) i₃ + 6800.Yo₂ - 3 = 0

6800.Yo₂ - 10100.Yo₃ = 3

Sistem Persamaan

-11300 i₁ + 9100.Yo₂ + 0.Yo₃= -18

9100.Yo₁ - 23400.Yo₂ + 6800.Yo₃ = 18

0.Yo₁ + 6800.Yo₂ - 10100.Yo₃ = 3

Walaupun bilangannya besar, ia cepat diselesaikan dengan bantuan kalkulator saintifik. Ingat bahawa persamaan mesti dipesan dan tambahkan sifar di tempat -tempat di mana yang tidak diketahui tidak muncul, seperti yang terdapat di sini.

Arus mesh adalah:

Yo₁ = 0.0012 A; Yo₂ = -0.00048 A; Yo₃ = -0.00062 a

Arus Yo₂ dan Yo₃ Mereka beredar ke arah yang bertentangan dalam angka itu, kerana mereka ternyata negatif.

Jadual arus dan voltan dalam setiap rintangan

Rintangan (Ω)	Semasa (amp)	Voltan = i.R (volt)
9100	Yo1 -Yo2 = 0.0012-(-0.00048) = 0.00168	lima belas.3
3300	0.00062	2.05
2200	0.0012	2.64
7500	0.00048	3.60
6800	Yo2 -Yo3= -0.00048-(-0.00062) = 0.00014	0.95

Penyelesaian Peraturan Cramer

Oleh kerana mereka adalah sejumlah besar, mudah untuk menggunakan notasi saintifik untuk bekerja dengan mereka secara langsung.

Pengiraan i₁

Anak panah warna dalam penentu 3 x 3 menunjukkan bagaimana mencari nilai berangka, mengalikan nilai yang ditunjukkan. Mari kita mulakan dengan mendapatkan pendakap pertama dalam penentu δ:

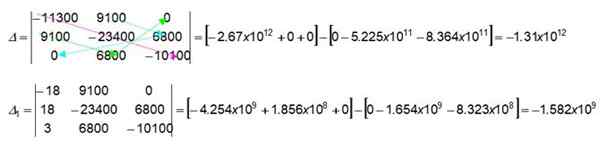
(-11300) x (-23400) x (-10100) = -2.67 x 10¹²

9100 x 0 x 0 = 0

9100 x 6800 x 0 = 0

Kami segera mendapatkan pendakap kedua dalam penentu yang sama, yang berfungsi dari kiri ke kanan (untuk kurungan ini anak panah berwarna tidak ditarik dalam angka itu). Kami menjemput pembaca untuk mengesahkannya:

0 x (-23400) x 0 = 0

9100 x 9100 x (-10100) = -8.364 x 10^sebelas

6800 x 6800 x (-11300) = -5.225 x 10^sebelas

Dengan cara yang sama, pembaca juga boleh mengesahkan nilai untuk penentu Δ₁.

Penting: Antara kedua kurungan selalu ada tanda negatif.

Akhirnya arus diperoleh Yo₁ melalui Yo₁ = Δ₁ / Δ

Yo₁ = -1.582 x 10⁹/-1.31 x 10¹² = 0.0012 a                                   

Pengiraan i₂

Prosedur boleh diulang untuk dikira Yo₂, Dalam kes ini, untuk mengira penentu δ₂ Lajur kedua penentu δ digantikan oleh lajur istilah bebas dan nilainya dijumpai, mengikut prosedur yang dijelaskan.

Walau bagaimanapun, seperti yang rumit kerana bilangan besar, terutamanya jika tidak ada kalkulator saintifik, yang paling mudah adalah untuk menggantikan nilai Yo₁ sudah dikira, dalam persamaan berikut dan jelas:

-11300 i₁ + 9100.Yo₂ + 0.Yo₃= -18 → 9100 i₂= -18 + 11300 i₁ → i₂ = -0.00048 a

Pengiraan i3

Sekali dengan nilai Yo₁ dan Yo₂ Di tangan, Yo₃ Ia ditemui secara langsung dengan penggantian.

Rujukan

1. Alexander, c. 2006. Asas Litar Elektrik. Ke -3. Edisi. MC Graw Hill.
2. Boylestad, r. 2011. Pengenalan kepada Analisis Litar.2. Edisi. Pearson.
3. Figueroa, d. (2005). Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 5. Interaksi elektrik. Diedit oleh Douglas Figueroa (USB).
4. Garcia, l. 2014. Elektromagnetisme. 2. Edisi. Universiti Perindustrian Santander.
5. Sears, Zemansky. 2016. Fizik universiti dengan fizik moden. Ke -14. Ed. Jilid 2.