Pertempuran tidak elok dalam dimensi dan contoh

The Kejutan tidak elok atau perlanggaran tidak elok adalah interaksi ringkas dan sengit antara dua objek di mana jumlah pergerakan dipelihara, tetapi bukan tenaga kinetik, yang mana peratusan berubah menjadi beberapa jenis tenaga yang lain.

Kejutan atau perlanggaran adalah kerap. Zarah subatomik bertembung pada kelajuan yang sangat tinggi, sementara banyak sukan dan permainan terdiri daripada perlanggaran berterusan. Malah galaksi mampu berlanggar.

Rajah 1. Perlanggaran kereta ujian. Sumber: Pixabay

Sebenarnya jumlah pergerakan dipelihara dalam apa -apa jenis perlanggaran, selagi zarah -zarah itu bertembung oleh sistem bertebat. Jadi dalam pengertian ini tidak ada masalah. Sekarang, objek mempunyai tenaga kinetik yang berkaitan dengan pergerakan yang mereka ada. Apa yang boleh berlaku dengan tenaga itu ketika terhempas?

Daya dalaman yang berlaku semasa pertembungan antara objek adalah sengit. Apabila dinyatakan bahawa tenaga kinetik tidak dipelihara, ini bermakna ia berubah menjadi jenis tenaga lain: contohnya, dalam tenaga bunyi (perlanggaran peranti mempunyai bunyi tersendiri).

Lebih banyak kemungkinan penggunaan tenaga kinetik: haba oleh geseran, dan tentu saja ubah bentuk yang tidak dapat dielakkan yang dialami oleh objek ketika berlanggar, seperti badan kereta dalam angka di atas.

[TOC]

Contoh perlanggaran tidak elok 

- Dua jisim plastik yang bertembung dan bertemu bersama, bergerak seperti satu keping selepas kemalangan.

- Bola getah yang melantun ke dinding atau lantai. Bola berubah apabila memberi kesan kepada permukaan.

Tidak semua tenaga kinetik berubah menjadi jenis tenaga lain, kecuali dalam beberapa pengecualian. Objek boleh kekal dengan jumlah tenaga ini. Kemudian kita akan melihat bagaimana mengira peratusan.

Apabila kepingan yang bertembung dikaitkan, perlanggaran itu dipanggil sempurna tidak elok, dan kedua -duanya biasanya bergerak bersama.

Perlanggaran yang tidak jelas dalam dimensi

Perlanggaran angka menunjukkan dua objek yang berbeza m₁ dan m₂, saling bergerak dengan kelajuan v_i1 dan v_I2 masing -masing. Segala -galanya berlaku pada mendatar, iaitu, ia adalah perlanggaran dalam dimensi, yang paling mudah untuk dikaji.

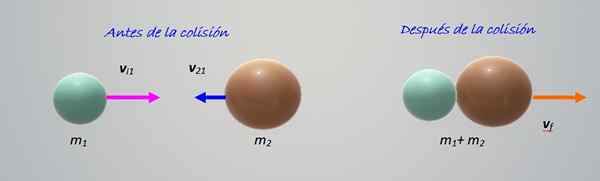Rajah 2. Perlanggaran antara dua zarah dari pelbagai orang. Sumber: Diri Diri.

Objek berlanggar dan kemudian bersatu pindah ke kanan. Ia adalah perlanggaran yang tidak sempurna, jadi sudah cukup bahawa kita menyimpan jumlah pergerakan:

P_{Sama ada} = P_F

Jumlah pergerakan adalah vektor yang unitnya n.s. Dalam situasi yang diterangkan, notasi vektor dapat dibebaskan dengan kerana ia adalah perlanggaran dalam dimensi:

Ia boleh melayani anda: Eksperimen Fizik Mudah (University Primer)

Mv_{Sama ada} = mv_F

Jumlah pergerakan sistem adalah jumlah vektor jumlah pergerakan setiap zarah.

m₁ v_i1  + m₂ v_I2 = (m₁ + m₂) v_F

Kelajuan akhir diberikan oleh:

v_F = (m₁ v_i1  + m₂ v_I2)/ (M₁ + m₂)

Pekali pemulihan

Terdapat jumlah yang dapat menunjukkan betapa elastik adalah perlanggaran. Ia mengenai pekali pemulihan, yang ditakrifkan sebagai nisbah negatif antara kelajuan relatif zarah selepas kemalangan dan kelajuan relatif sebelum kemalangan.

Biarkan awak₁ dan anda₂ Kelajuan zarah masing -masing pada mulanya. Dan menjadi v₁ dan v₂ kelajuan akhir masing -masing. Secara matematik pekali restitusi boleh dinyatakan seperti berikut:

Koefisien pengembalian adalah jumlah tambahan, kerana ia adalah nisbah antara kelajuan. Tetapi maklumat yang diberikan sangat menarik:

- Jika ε = 0 bersamaan dengan menyatakan bahawa v₂ = v₁. Ini bermaksud bahawa kelajuan akhir adalah sama dan pertembungan tidak elok, seperti yang diterangkan dalam bahagian sebelumnya.

- Bila ε = 1 bermaksud bahawa kelajuan relatif baik sebelum dan selepas kemalangan tidak berubah, dalam hal ini pertembungan elastik.

- Dan jika 0 < ε < 1 parte de la energía cinética de la colisión se transforma en alguna otra de las energías mencionadas anteriormente.

Cara menentukan pekali pengembalian?

Koefisien pengembalian bergantung kepada kelas bahan yang terlibat dalam perlanggaran. Ujian yang sangat menarik untuk menentukan bagaimana elastik adalah bahan untuk membuat bola adalah menjatuhkan bola di permukaan tetap dan mengukur ketinggian pemulihan.

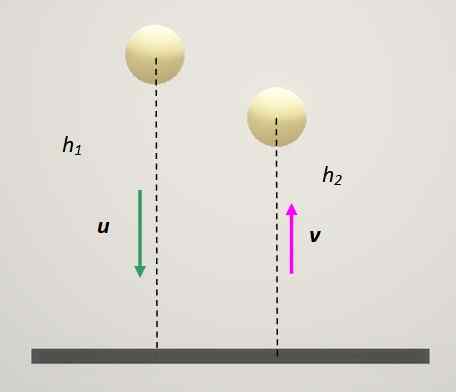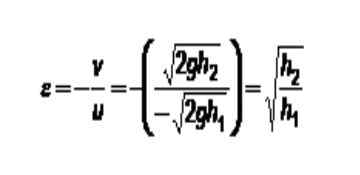
Rajah 3. Kaedah untuk menentukan pekali restitusi. Sumber: Diri Diri.

Dalam kes ini, plat tetap selalu mempunyai kelajuan 0. Jika indeks 1 ini diberikan kepada ini dan bola adalah: Indeks 2 kekal:

Kelajuan awal bergantung pada ketinggian h₁ dari mana dia jatuh:

Tanda negatif menunjukkan arah ke bawah. Dan kelajuan akhir berkaitan dengan ketinggian maksimum h₂ yang sampai dalam pemulihan:

Menggantikan pekali restitusi yang anda ada:

Letupan

Pada mulanya ia telah dicadangkan bahawa semua tenaga kinetik dapat diubah dengan bergerak ke jenis tenaga lain. Lagipun, tenaga tidak dimusnahkan. Adakah mungkin objek yang datang dengan pergerakan bertabrakan dan bergabung bersama membentuk satu objek yang tiba -tiba berehat? Ini tidak begitu mudah dibayangkan.

Ia boleh melayani anda: Dinamik: Sejarah, Kajian, Undang -undang dan Teori Apa

Namun, mari kita bayangkan apa yang berlaku ke belakang, seperti dalam filem yang dilihat di belakang. Kemudian objek pada mulanya berehat dan kemudian meletupkan pemecahan ke beberapa bahagian. Keadaan ini sangat mungkin: ia adalah letupan.

Supaya letupan dapat dianggap sebagai perlanggaran yang tidak sempurna yang dilihat ke belakang dalam masa. Jumlah pergerakan juga dipelihara, dapat mengesahkannya:

P_{Sama ada} = P_F

Contoh yang diselesaikan

-Latihan 1

Dikenali dari pengukuran bahawa pekali pengembalian keluli adalah 0.90. Bola keluli dijatuhkan dari 7 m tinggi pada pinggan tetap. Kira:

a) Sehingga ketinggian apa yang akan melantun.

b) Berapa lama masa antara hubungan pertama dengan permukaan dan yang kedua.

Penyelesaian

a) Persamaan yang sebelum ini disimpulkan dalam bahagian mengenai penentuan pekali restitusi digunakan:

Ketinggian lenyap h₂:

0.90² . 7 m = 5.67 m

b) Meningkatkan 5.67 meter kelajuan yang diberikan oleh:

Dari mana:

Dan masa yang diperlukan untuk mencapai ketinggian ini adalah:

t _Maks = v_{Sama ada}/ g = (10.54/9.8 s) = 1.08 s.

Masa yang diperlukan untuk kembali adalah sama, oleh itu jumlah masa untuk memuat naik 5.67 meter dan kembali ke titik permulaan adalah dua kali ganda masa maksimum:

t_penerbangan = 2.15 s.

-Latihan 2

Angka ini menunjukkan blok kayu massa yang tergantung pada selebihnya benang panjang l sebagai pendulum. Ini dipanggil pendulum balistik dan berfungsi untuk mengukur kelajuan v kemasukan jisim jisim m. Semakin tinggi kelajuan yang mana peluru memberi kesan kepada blok, pada ketinggian yang lebih tinggi h ini akan dibina.

Peluru imej tertanam di blok, oleh itu ia adalah kejutan yang tidak jelas.

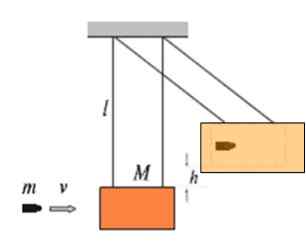Rajah 4. Pendulum balistik.

Menganggap bahawa 9 9.72 g kesan terhadap blok jisim 4.60 kg, maka set naik ke 16.8 cm kedudukan keseimbangan. Apakah kelajuannya v peluru?

Penyelesaian

Semasa perlanggaran jumlah pergerakan dipelihara dan atau_F Ia adalah kelajuan set, apabila peluru telah tertanam di blok:

P_{Sama ada} = P_F

Blok pada mulanya berehat, sementara peluru diarahkan ke sasaran dengan kelajuan v:

m.v + m.0 = (m + m) u_F

 

Ia tidak diketahui atau_F Malah, tetapi selepas perlanggaran, tenaga mekanikal dipelihara, ini menjadi jumlah tenaga potensi graviti dan tenaga kinetik k:

Boleh melayani anda: Jumlah vektor: kaedah grafik, contoh, latihan yang diselesaikan

Tenaga Mekanikal Awal = Tenaga Mekanikal Akhir

Dan_mo = E_Mf

Atau_{Sama ada} + K_{Sama ada} = U_F + K_F

Tenaga potensi graviti bergantung pada ketinggian di mana set mencapai. Untuk kedudukan keseimbangan ketinggian awal adalah yang diambil sebagai tahap rujukan, oleh itu:

Atau_{Sama ada} = 0

Terima kasih kepada peluru, set mempunyai tenaga kinetik K_{Sama ada}, yang menjadi tenaga potensi graviti apabila set mencapai ketinggian maksimumnya h. Tenaga kinetik diberikan oleh:

K = ½ mV²

Pada mulanya tenaga kinetik adalah:

K_{Sama ada} = (1/2) (m+m) u_F²

Ingat bahawa peluru dan blok membentuk objek massa tunggal M+ m. Tenaga potensi graviti apabila mereka mencapai ketinggian maksimum adalah:

Atau_F = (m + m) gh

Oleh itu:

K_{Sama ada} = U_F

(1/2) (m+m) u_F² = (m + m) gh

Sekarang hasil ini diganti dalam ekspresi ke v yang dibersihkan pada mulanya, dari pemuliharaan jumlah pergerakan:

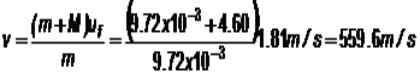
-Latihan 3

Objek angka meletup dalam tiga serpihan: dua jisim yang sama m dan satu lebih besar jisim 2m. Angka ini menunjukkan kelajuan setiap serpihan selepas letupan. Apakah objektif awal objek?

Rajah 5. Batu yang meletup dalam 3 serpihan. Sumber: Diri Diri.

Penyelesaian

Masalah ini memerlukan penggunaan dua koordinat: x dan dan, Kerana dua serpihan mempunyai kelajuan menegak, sementara baki mempunyai kelajuan mendatar.

Jumlah jisim objek adalah jumlah jisim semua serpihan:

M = m + m + 2m = 4m

Jumlah pergerakan dipelihara pada paksi x dan pada paksi y, ia dicadangkan secara berasingan:

1. 4m. atau_x= m v₃
2. 4m. atau_dan = m. 2v₁ - 2m. v₁

Perhatikan bahawa serpihan besar bergerak ke bawah dengan kelajuan V1, untuk menunjukkan fakta ini tanda negatif telah diletakkan.

Dari persamaan kedua ia segera mengikutinya atau_dan = 0, Dan yang pertama jelas UX dengan segera:

Objektif awal objek adalah u_{Sama ada} = u_x = v₃/4.

Rujukan

1. Giancoli, d.  2006. Fizik: Prinsip dengan aplikasi. 6^th. Ed Prentice Hall. 175-181
2. Rex, a. 2011. Asas Fizik. Pearson. 135-155.
3. Serway, r., Vulle, c. 2011. Asas Fizik. 9^na Pembelajaran Cengage. 172 -182
4. Tipler, ms. (2006) Fizik untuk Sains dan Teknologi. Edisi ke -5. Jilid 1. Editorial kembali. 217-238
5. Tippens, ms. 2011. Fizik: Konsep dan aplikasi. Edisi ke -7. Macgraw Hill. 185 -195