Jenis litar semasa, aplikasi, contoh

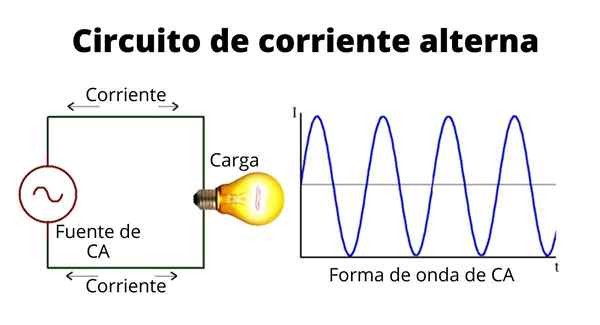
The Litar semasa berselang -seli Sama ada Litar CA Mereka terdiri daripada gabungan unsur -unsur rintangan, induktif dan kapasitif, digabungkan dengan sumber voltan alternatif, yang biasanya sinusoidal.

Apabila menggunakan voltan, arus pembolehubah ditubuhkan untuk masa yang singkat, yang dipanggil arus sementara, yang memberi laluan kepada arus pegun sinusoidal.

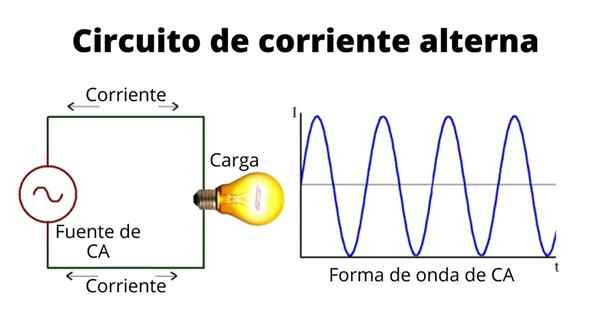Litar semasa berselang

Arus sinusoidal mempunyai nilai -nilai yang bergantian antara positif dan negatif, berubah menjadi selang masa yang tetap yang ditentukan oleh kekerapan yang telah ditetapkan sebelumnya. Bentuk arus dinyatakan sebagai:

I (t) = i_m Sen (ωt --φ)

Di mana saya_m Ia adalah arus maksimum atau amplitud semasa, Ω adalah kekerapan, t Sudah tiba masanya dan φ perbezaan fasa. Unit -unit yang biasa digunakan untuk arus adalah amps (a) dan submulitnya, seperti milliamperium dan microamperium.

Bagi bahagiannya, masa diukur dalam beberapa saat, kerana kekerapan adalah Hertzios atau Hertz, Hz disingkat, sementara perbezaan fasa adalah sudut yang biasanya diukur dalam radians, walaupun kadang -kadang kadang -kadang terjadi dalam darjah. Baik ini mahupun radian dianggap unit.

Simbol yang digunakan untuk sumber voltan alternatif

Lazimnya voltan alternatif dilambangkan dengan gelombang di dalam bulatan, untuk membezakannya dari voltan langsung, yang dilambangkan oleh dua garis yang tidak sama rata dan selari.

[TOC]

Jenis litar semasa berselang

Terdapat banyak jenis litar semasa yang berselang -seli, bermula dengan litar paling mudah yang ditunjukkan dalam angka berikut. Dari kiri ke kanan mereka mempunyai:

-Hormat dengan rintangan r

-Litar dengan gegelung l

-Litar dengan kondensator c.

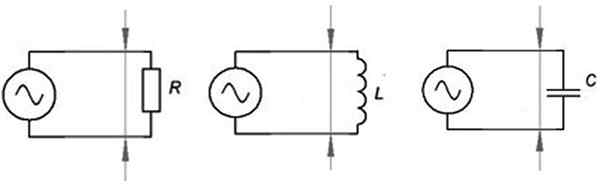Dari kiri ke kanan: litar kapasiti yang rintangan, induktif dan terakhir. Sumber: f. Zapata.

Litar dengan elemen rintangan

Dalam litar dengan rintangan r yang disambungkan ke sumber voltan alternatif, voltan rintangan ialah v_R = V_m Sen ωt. Oleh undang -undang ohm, yang juga sah untuk litar semata -mata rintangan semasa berselang -seli:

V_R = I_R∙ r

Oleh itu arus maksimum i_m = V_m /R.

Kedua -dua arus dan voltan berada dalam fasa, yang bermaksud bahawa mereka mencapai nilai maksimum mereka, dan juga 0, pada masa yang sama.

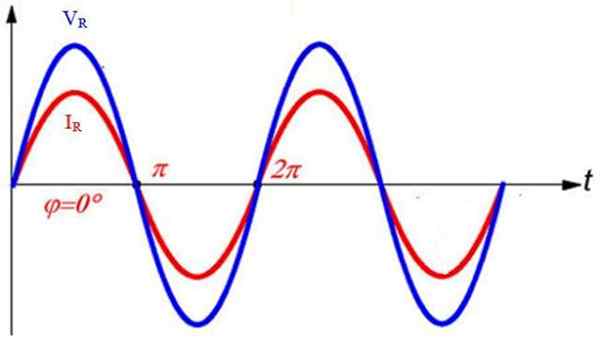Dalam litar semasa bergantian semata -mata, arus dan rintangan berada dalam fasa. Sumber: f. Zapata.

Litar elemen induktif

Dalam gegelung l, voltan adalah v_L = V_m Sen ωt dan berkaitan dengan arus dalam induktor melalui persamaan:

Mengintegrasikan:

Untuk sifat alasan trigonometri, i_L Ia ditulis dari segi dosa sebagai:

Yo_L = I_m dosa (ωt - ½ π)

Boleh melayani anda: satelit semula jadi

Kemudian, voltan dan arus sudah lapuk, yang terakhir ditangguhkan ½ π = 90º berkenaan dengan voltan (arus bermula sebelum ini, iaitu T = 0 s titik permulaan). Ini dilihat dalam angka berikut berbanding dengan sinusoid i_L dan v_L:

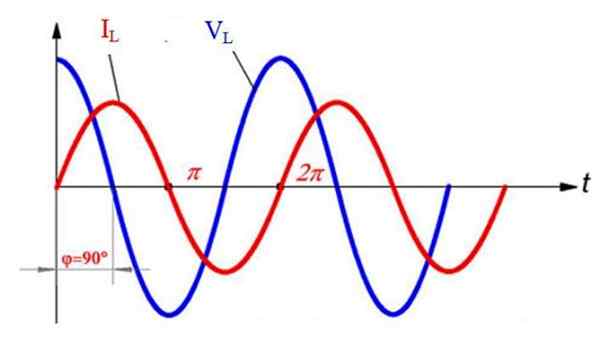Voltan dan arus alternatif dalam litar semasa berselang -seli yang semata -mata induktif. Sumber: f. Zapata.

Reaktansi induktif

Reaktan induktif ditakrifkan sebagai x_L = ΩL, meningkat dengan kerap dan mempunyai dimensi rintangan, oleh itu, dalam analogi dengan undang -undang ohm:

V_L = I_L ∙ x_L

Litar dengan elemen kapasitif

Untuk con casser c yang disambungkan ke sumber semasa yang berselang -seli, ia dipenuhi bahawa:

Q = C ∙ V_C = C ∙ v_m Sen ωt

Semasa dalam kondensor memperoleh beban berkenaan dengan masa:

Yo_C= ωc ∙ v_m cos ωt

Tetapi cos ωt = sin (ωt + ½ π), kemudian:

Yo_C = Ωcv_m dosa (ωt+ ½ π)

Dalam kes ini, kemajuan semasa ke voltan dalam ½ π, seperti yang dapat dilihat dari grafik.

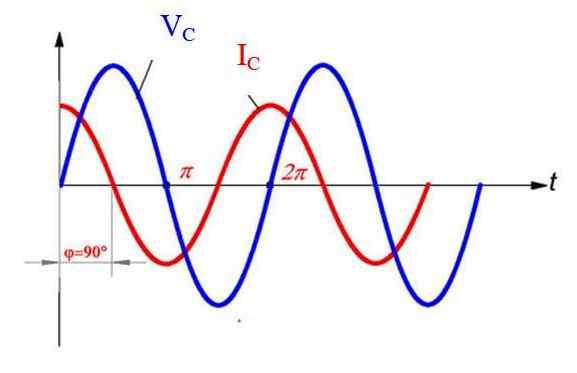Voltan dan arus dalam litar alternatif dengan elemen kapasitif semata -mata. Sumber: f. Zapata.

Reaktansi kapasitif

Reaktansi kapasitif boleh ditulis x_C = 1/Ωc, berkurangan dengan kekerapan dan juga mempunyai unit rintangan, iaitu, ohm. Dengan cara ini, undang -undang ohm seperti ini:

V_C = X_C.Yo_C

Aplikasi

Michael Faraday (1791-1867) adalah yang pertama untuk mendapatkan arus yang secara berkala mengubah maknanya, melalui eksperimen induksi, walaupun pada hari-hari awal, hanya arus langsung digunakan.

Pada akhir abad ke -19, perang arus yang terkenal, antara Thomas hingga. Edison, Defender Penggunaan Arus Langsung dan George Westinghouse, penyokong arus berselang. Akhirnya ini adalah yang dimenangi oleh ekonomi, kecekapan dan kemudahan penghantaran dengan kerugian kecil.

Atas sebab ini setakat ini, arus yang datang ke rumah dan industri adalah semasa berselang -seli, walaupun penggunaan arus langsung tidak pernah hilang sepenuhnya.

Arus seli digunakan untuk hampir segala -galanya, dan dalam banyak aplikasi, perubahan arah arus seli yang berterusan tidak relevan, seperti mentol lampu, besi atau tanduk masak, kerana pemanasan unsur rintangan itu tidak bergantung pada arah pergerakan beban.

Sebaliknya, hakikat bahawa perubahan semasa yang bermaksud dengan kekerapan tertentu adalah asas motor elektrik dan pelbagai aplikasi yang lebih spesifik, seperti yang berikut:

Ia dapat melayani anda: penyebaran bunyi

Litar pelfming

Litar yang terdiri daripada sumber alternatif yang disambungkan ke rintangan dan kapasitor bersiri dikenali sebagai litar siri RC dan digunakan untuk menghapuskan garis yang tidak diingini dalam litar lain, atau juga menambah beberapa kesan khas untuk ini.

Mereka juga berfungsi sebagai pembahagi voltan dan untuk menyesuaikan diri di stesen radio (lihat Contoh 1 di bahagian seterusnya).

Litar jenis jambatan

Litar jambatan yang diberi makan arus berganti boleh digunakan untuk mengukur kapasiti atau induktansi, dengan cara yang sama bahawa jambatan wheatstone digunakan, litar semasa langsung yang terkenal yang mampu mengukur nilai rintangan yang tidak diketahui.

Contoh litar semasa berselang

Di bahagian sebelumnya, litar semasa yang paling mudah digambarkan, walaupun sudah tentu, unsur -unsur asas yang diterangkan di atas, dan juga yang lain sedikit lebih kompleks seperti diod, penguat dan transistor, untuk menamakan beberapa, boleh digabungkan untuk mendapatkan pelbagai kesan.

Contoh 1: Litar RLC

Salah satu litar yang paling biasa di Ac Ia adalah yang merangkumi rintangan r, gegelung atau induktor l dan siri kapasitor atau kondensor dengan sumber semasa.

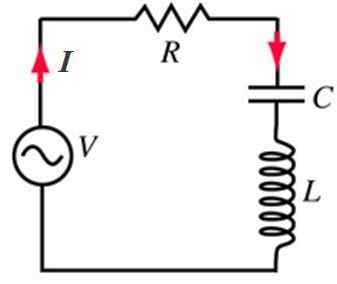Litar RLC dalam siri diberi makan dengan sumber semasa yang berselang -seli. Sumber: f. Zapata.

Litar siri RLC bertindak balas terutamanya kepada kekerapan sumber alternatif yang mereka makan. Itulah sebabnya salah satu aplikasi yang paling menarik adalah seperti litar yang ditala radio.

Isyarat radio kerap menjana arus dengan kekerapan yang sama dalam litar yang direka khas untuk berfungsi sebagai penerima, dan amplitud arus ini adalah maksimum jika penerima ditala dengan kekerapan itu, melalui kesan yang dipanggil resonans.

Litar penerimaan berfungsi sebagai penala kerana ia direka supaya isyarat frekuensi yang tidak diingini menghasilkan arus yang sangat kecil, yang tidak dikesan oleh penceramah radio dan oleh itu tidak boleh didengar. Sebaliknya, ke frekuensi resonans, amplitud arus mencapai maksimum dan kemudian isyarat jelas didengar.

Kekerapan resonans berlaku apabila reaksi induktif dan kapasitif litar disamakan:

X_L = X_C

1/ωc = ΩL

Ω² = 1/lc

Stesen radio dengan isyarat frekuensi Ω dikatakan "ditala", dan nilai l dan c dipilih untuk kekerapan tertentu.

Ia boleh melayani anda: usaha biasa: Apa yang terdiri daripada, bagaimana ia dikira, contohnya

Contoh 2: Litar RLC selari

Litar RLC selari juga mempunyai respons tertentu mengikut kekerapan sumber, yang bergantung kepada reaksi setiap elemen, yang ditakrifkan sebagai alasan antara voltan dan arus.

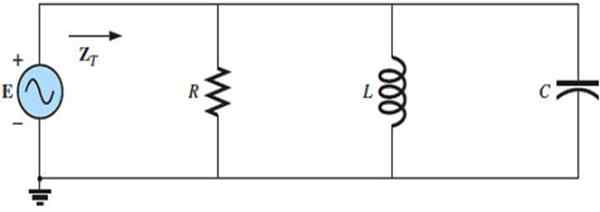Litar RLC secara selari dihubungkan dengan sumber semasa yang berselang -seli. Sumber: f. Zapata.

Latihan diselesaikan

Dalam litar LRC dalam siri 1 bahagian sebelumnya, rintangan bernilai 200 ohm, induktansi 0.4 jam dan kondensor adalah 6 μF. Bagi bahagiannya, bekalan kuasa adalah voltan amplitud alternatif yang sama dengan 30 V, selalunya 250 rad/s. Diminta untuk mencari:

a) reaksi setiap elemen

b) Nilai modul impedans litar.

c) amplitud semasa

Penyelesaian kepada

Reaksi masing -masing dikira dengan formula:

X_C = 1/ωc = 1/(250 rad/s x 6 x10^-6 F) = 666.67 ohm

X_L = ΩL = 250 rad/s x 0.4 H = 100 ohm

Dan reaksi rintangan bersamaan dengan nilainya dalam ohm:

X_R = R = 200 ohm

Penyelesaian b

Impedans Z ditakrifkan sebagai sebab antara voltan dan arus dalam litar, sama ada dalam siri atau selari:

Z = v_m / Yo_m

Impedans diukur dalam ohm, serta rintangan atau reaksi, tetapi merujuk kepada pembangkang terhadap laluan arus induktansi dan kapasitor, memandangkan sebagai tambahan kepada kesan tertentu, seperti melambatkan atau memajukan voltan, juga mereka juga mempunyai rintangan dalaman tertentu.

Ia dapat ditunjukkan bahawa untuk litar siri RLC, modul impedans diberikan oleh:

Apabila menilai nilai yang diberikan dalam pernyataan, ia diperolehi:

Penyelesaian c

Dari:

Z = v_m / Yo_m

Ia perlu;

Yo_m = V_m / Z = 30V / 601 ohms = 0.05 a.

Tema minat

Perbezaan antara arus bergantian dan langsung

Rujukan

1. Alexander, c. 2006. Asas Litar Elektrik. Ke -3. Edisi. MC Graw Hill.
2. Boylestad, r. 2011. Pengenalan kepada Analisis Litar.2. Edisi. Pearson.
3. Figueroa, d. (2005). Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 6. Elektromagnetisme. Diedit oleh Douglas Figueroa (USB).
4. Sears, Zemansky. 2016. Fizik universiti dengan fizik moden. Ke -14. Ed. Jilid 1. Pearson.
5. Serway, r., Jewett, J. (2008). Fizik untuk Sains dan Kejuruteraan. Jilid 1. Ke -7. Ed. Pembelajaran Cengage.