Bagaimana mendapatkan sudut segitiga? (Contoh)

Terdapat pelbagai cara Kirakan sisi dan sudut segitiga. Ini bergantung pada jenis segitiga yang anda kerjakan.

Pada kesempatan ini, ia akan ditunjukkan bagaimana untuk mengira sisi dan sudut segitiga yang betul, dengan mengandaikan bahawa data segitiga tertentu dengan kenalan dengan kenalan.

Unsur -unsur yang akan digunakan adalah:

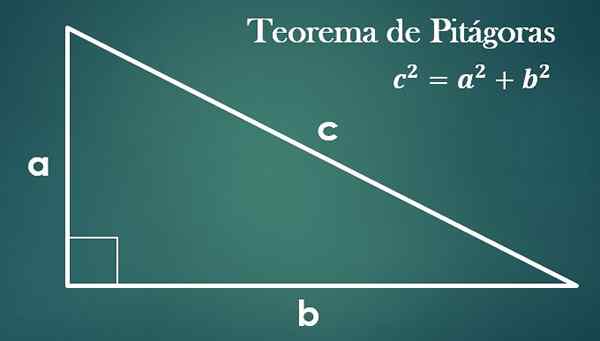
- Teorem Pythagoras

Memandangkan segitiga segi empat tepat dengan "a", "b" dan hypotenusa "c", memang benar bahawa "c² = a²+b²".

- Kawasan segitiga

Formula untuk mengira kawasan mana -mana segitiga adalah a = (b × h)/2, di mana "b" adalah panjang asas dan "h" panjang ketinggian.

- Sudut segitiga

Jumlah tiga sudut dalaman segitiga adalah 180 °.

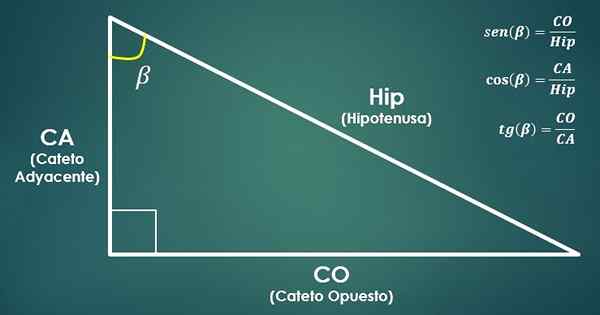
- Fungsi Trigonometrik:

Pertimbangkan segitiga yang betul. Kemudian, fungsi trigonometri ditakrifkan sinus, kosinus dan tangen sudut beta (β) seperti berikut:

sin (β) = co/hip, cos (β) = ca/hip dan tan (β) = co/ca.

Cara mengira sisi dan sudut segitiga yang betul?

Memandangkan segitiga segi empat tepat ABC, situasi berikut boleh dibentangkan:

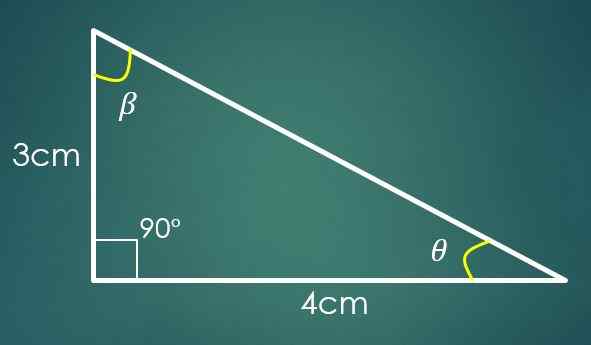
1- Dua kaki dikenali

Jika Cateto "A" mengukur 3 cm dan Cateto "B" berukuran 4 cm, maka untuk mengira nilai "C" teorem Pythagoras digunakan. Dengan menggantikan nilai "A" dan "B" ia diperolehi bahawa C² = 25 cm², yang menunjukkan bahawa C = 5 cm.

Sekarang, jika sudut β bertentangan dengan kategori "B", maka dosa (β) = 4/5. Apabila menggunakan fungsi terbalik payudara, dalam kesamaan terakhir ini diperolehi bahawa β = 53,13º. Dua sudut dalaman segitiga sudah diketahui.

Biarkan θ menjadi sudut yang masih diketahui, maka 90º+53.13º+θ = 180 °, di mana ia diperolehi yang θ = 36.87º.

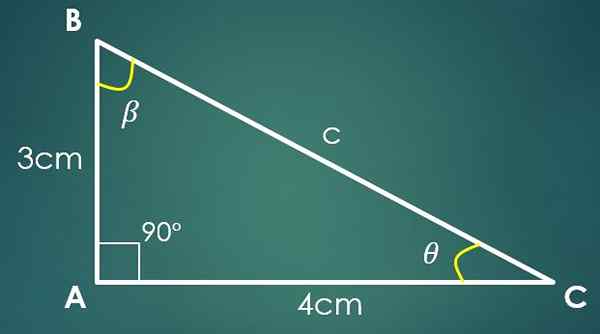
Dalam kes ini, tidak perlu bagi pihak yang diketahui untuk menjadi dua kaki, perkara penting adalah untuk mengetahui nilai mana -mana dua pihak.

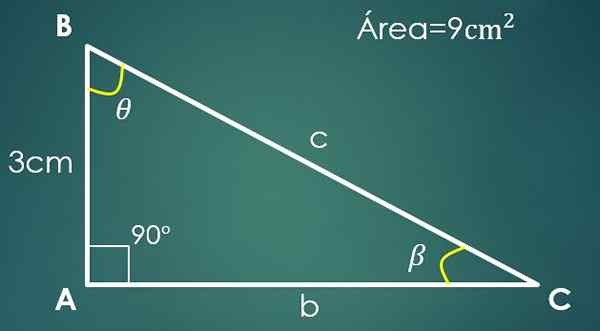
2- Kaki dan kawasannya dikenali

Biarkan a = 3 cm kaki yang diketahui dan 9 cm² kawasan segitiga.

Dalam segi empat segi empat tepat kategori boleh dianggap sebagai asas dan yang lain sebagai ketinggian (kerana mereka berserenjang).

Katakan bahawa "a" adalah asas, oleh itu, 9 = (3 × h)/2, di mana ia diperolehi bahawa kategori lain berukuran 6 cm. Untuk mengira hipotenus, teruskan seperti dalam kes sebelumnya, dan diperolehi bahawa C = √45 cm.

Sekarang, jika sudut β bertentangan dengan cateto "A", maka dosa (β) = 3/√45. Apabila membersihkan β diperoleh bahawa nilainya ialah 26.57º. Anda hanya perlu mengetahui nilai sudut ketiga θ.

Ia dipenuhi bahawa 90 °+26.57º+θ = 180 °, di mana ia disimpulkan bahawa θ = 63.43º.

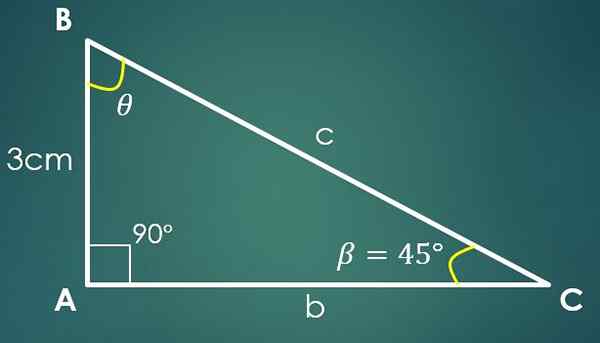
3- Sudut dan Cateto dikenali

Biarkan β = 45 ° sudut yang diketahui dan a = 3 cm kaki yang diketahui, di mana Cateto "A" menentang sudut β. Menggunakan formula tangen, diperoleh bahawa Tg (45 °) = 3/ca, di mana ternyata Ca = 3 cm.

Menggunakan teorem pythagoras, diperolehi bahawa c² = 18 cm², iaitu, c = 3√2 cm.

Telah diketahui bahawa sudut berukuran 90 ° dan β mengukur 45 °, dari sini disimpulkan bahawa sudut ketiga berukuran 45 °.

Dalam kes ini, bahagian yang diketahui tidak perlu menjadi kaki, ia boleh menjadi mana -mana tiga sisi segitiga.