Koordinat Silinder Sistem, Perubahan dan Latihan

The Koordinat silinder Mereka berkhidmat untuk mencari mata di ruang tiga dimensi dan terdiri daripada koordinat radial ρ, koordinat azimutal φ dan koordinat ketinggian z.

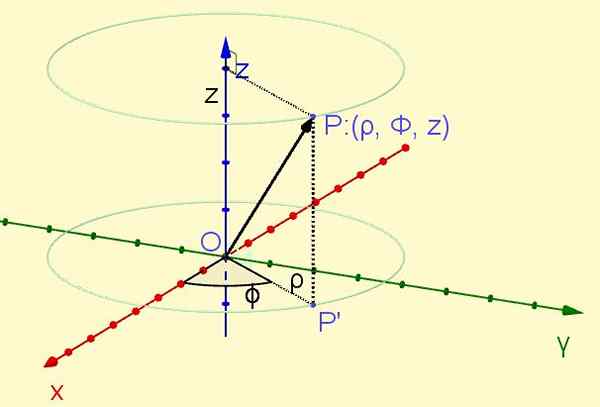
Titik P Terletak di ruang angkasa diunjurkan secara ortogon di atas kapal terbang Xy menimbulkan titik P ' Dalam pesawat itu. Jarak dari asal ke titik P ' mentakrifkan koordinat ρ, manakala sudut yang membentuk paksi X Dengan separuh masa Op ' Tentukan koordinat φ. Akhirnya, koordinat z Ia adalah unjuran ortogonal pada titik P pada paksi Z. (Lihat Rajah 1).

Rajah 1. Titik P koordinat silinder (ρ, φ, z). (Huraian sendiri)

Koordinat radial ρ sentiasa positif, koordinat azimutal φ bervariasi dari sifar radians hingga dua radian Pi, manakala koordinat Z boleh mengambil apa -apa nilai sebenar:

0 ≤ ρ < ∞

0 ≤ φ < 2π

- ∞ < z < + ∞

[TOC]

Perubahan koordinat

Ia agak mudah untuk mendapatkan koordinat Cartesian (x, y, z) dari titik P dari koordinat silindernya (ρ, φ, z):

x = ρ cos (φ)

y = ρ sen (φ)

z = z

Tetapi ia juga mungkin untuk mendapatkan koordinat kutub (ρ, φ, z) berdasarkan pengetahuan koordinat Cartesian (x, y, z) dari titik p:

ρ = √ (x² + dan²)

φ = arctan (y/x)

z = z

Asas vektor dalam koordinat silinder

Pangkalan vektor silinder ditakrifkan Uρ, Uφ, UZ.

Vektor Uρ Ia adalah tangen ke garisan φ = ctte dan z = ctte (menunjuk secara radiasi), vektor Uφ adalah tangen ke garisan ρ = ctte dan z = ctte dan akhirnya UZ Ia mempunyai arah yang sama dari paksi z.

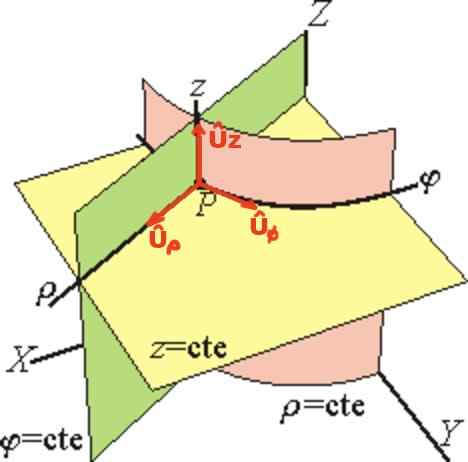Rajah 2. Pangkalan koordinat silinder. (Wikimedia Commons)

Di pangkalan unit silinder, vektor kedudukan r Dari titik p ia ditulis vektor seperti ini:

Ia dapat melayani anda: domain dan percanggahan fungsi (dengan contoh)

r = ρ Uρ + 0 Uφ + z UZ

Sebaliknya, anjakan yang sangat kecil dr Dari titik P ia dinyatakan seperti berikut:

dr = Dρ Uρ + ρ dφ  Uφ + Dz UZ

Begitu juga, unsur infinitesimal volum DV dalam koordinat silinder adalah:

Dv = ρ dρ dφ dz

Contoh

Terdapat banyak contoh penggunaan dan penggunaan koordinat silinder. Dalam kartografi, sebagai contoh, unjuran silinder, berdasarkan tepat pada koordinat ini. Terdapat lebih banyak contoh:

Contoh 1

Koordinat silinder mempunyai aplikasi dalam teknologi. Sebagai contoh, anda mempunyai sistem data CHS (silinder-head-sektor) lokasi data pada cakera keras, yang sebenarnya terdiri daripada beberapa cakera:

- Silinder atau trek sepadan dengan menyelaras ρ.

- Sektor ini sepadan dengan kedudukan φ album yang berputar di Tinggi halaju sudut.

- Kepala sepadan dengan kedudukan Z kepala bacaan pada album yang sepadan.

Setiap byte maklumat mempunyai alamat yang tepat dalam koordinat silinder (c, s, h).

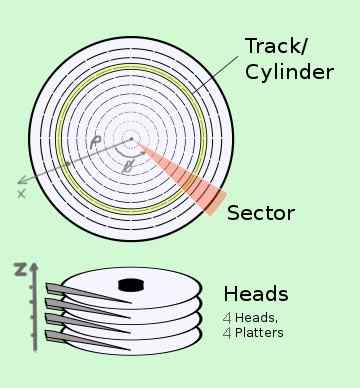Rajah 2. Lokasi maklumat dalam koordinat silinder dalam sistem cakera keras. (Wikimedia Commons)

Contoh 2

Kren pembinaan menetapkan kedudukan beban dalam koordinat silinder. Kedudukan mendatar ditakrifkan dengan jarak ke paksi kren atau anak panah. Kedudukan menegak beban ditentukan oleh koordinat z ketinggian.

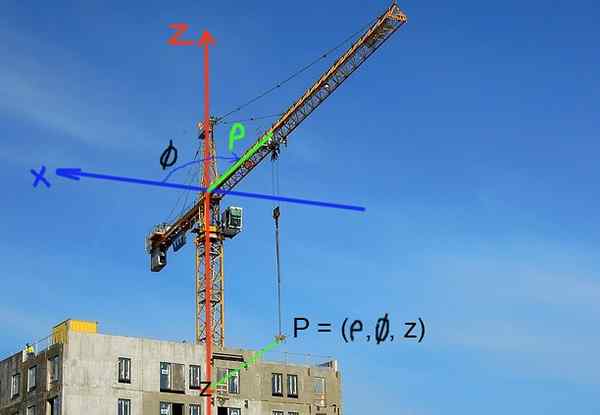Rajah 3. Kedudukan beban dalam kren pembinaan dapat dengan mudah dinyatakan dalam koordinat silinder. (Imej Pixabay - RCOS R. Pérez)

Latihan yang diselesaikan

Latihan 1

Terdapat titik P1 koordinat silinder (3, 120º, -4) dan titik P2 koordinat silinder (2, 90º, 5). Cari Jarak Euclidian Antara kedua -dua mata ini.

Boleh melayani anda: bahagian di mana sisa adalah 300

Penyelesaian: Pertama, kita teruskan mencari koordinat Cartesian setiap titik berikutan formula yang berlaku di atas.

P1 = (3* cos 120º, 3* sen 120º, -4) = (-1.5, 2.60, -4)

P2 = (2* cos 90º, 2* sin 90º, 5) = (0, 2, 5)

Jarak Euclidian antara P1 dan P2 adalah:

D (p1, p2) = √ ((0 - (-1.5))²+(2 - 2.60)²+(5 -(-4))² ) = ..

... √ (2.25+0.36+81) = 9.14

Latihan 2

Point P mempunyai koordinat Cartesian (-3, 4, 2). Cari koordinat silinder yang sepadan.

Penyelesaian: Koordinat silinder didapati menggunakan hubungan yang diberikan di atas:

ρ = √ (x² + dan²) = √ ((-3)² + 4²) = √ (9 + 16) = √ (25) = 5

φ = arctan (y/x) = arcan (4/(-3)) = -53.13º + 180º = 126.87º

Z = 2

Harus diingat bahawa fungsi arcangent adalah multivalueada berkala 180º. Di samping itu, sudut φ mesti tergolong dalam kuadran kedua, kerana x e y dan koordinat titik p berada di kuadran itu. Inilah sebab mengapa 180º telah ditambah kepada hasilnya φ.

Latihan 3

Ekspres dalam koordinat silinder dan di Cartesian menyelaraskan permukaan silinder radio 2 dan paksi yang bertepatan dengan paksi z.

Penyelesaian: Difahamkan bahawa silinder mempunyai lanjutan tak terhingga dalam arah z, supaya persamaan permukaan tersebut dalam koordinat silinder adalah:

ρ = 2

Untuk mendapatkan persamaan Cartesian permukaan silinder, kuadrat kedua -dua anggota persamaan sebelumnya diambil:

ρ² = 4

Kami membiak dengan 1 kedua -dua ahli kesamaan sebelumnya dan memohon Identiti trigonometri asas (Sen²(φ) + cos²(φ) = 1):

1 * ρ² = 1 * 4

(Sen²(φ) + cos²(φ)) * ρ² = 1 * 4

Pandangan ini berkembang untuk mendapatkan:

(ρ sen (φ))² + (ρ cos (φ))² = 4

Boleh melayani anda: penduduk dan sampel

Kita ingat bahawa kurungan pertama (ρ sen (φ)) adalah koordinat dan titik dalam koordinat kutub, manakala kurungan (ρ cos (φ)) mewakili koordinat x, sehingga kita telah meninggalkan Persamaan silinder dalam koordinat Cartesian:

dan² + x² = 2²

Persamaan sebelumnya tidak boleh dikelirukan dengan bulatan dalam satah XY, kerana dalam kes ini ia akan menjadi seperti ini: dan² + x² = 2² ; Z = 0.

Latihan 4

Silinder radius r = 1 m dan ketinggian H = 1m mempunyai jisim yang diedarkan secara radiasi mengikut persamaan berikut d (ρ) = c (1 - ρ/r) di mana c adalah nilai c = 1 kg/m³. Cari jumlah jisim silinder dalam kilogram.

Penyelesaian: Perkara pertama adalah untuk menyedari bahawa fungsi d (ρ) mewakili ketumpatan massa volumetrik, dan jisim ketumpatan diedarkan dalam cascarones silinder untuk mengurangkan ketumpatan pusat ke pinggir. Unsur yang sangat kecil dari kelantangan mengikut simetri masalahnya ialah:

Dv = ρ dρ 2π h

Dari sana anda perlu, jisim infinitesimal dari shell silinder akan menjadi:

Dm = d (ρ) dv

Oleh itu, jumlah jisim silinder akan dinyatakan oleh yang berikut Integral yang ditakrifkan:

M = ∫_{Sama ada}^R D (ρ) dv = ∫_{Sama ada}^R C (1 - ρ/r) ρ dρ 2π H = 2π h c ∫_{Sama ada}^R (1 - ρ/r) ρ dρ

Penyelesaian integral yang ditunjukkan tidak sukar diperoleh, sebagai hasilnya:

∫_{Sama ada}^R (1 - ρ/r) ρ dρ = (⅙) r²

Menggabungkan hasil ini dalam ekspresi jisim silinder diperolehi:

M = 2π h c (⅙) r² = ⅓ π h c r² =

 ⅓ π 1m*1kg/m³* 1m² = π/3 kg ≈ 1.05 kg

Rujukan

1. Arfken G dan Weber H. (2012). Kaedah matematik untuk ahli fizik. Panduan komprehensif. Edisi ke -7. Akhbar Akademik. ISBN 978-0-12-384654-9
2. Pengiraan CC. Masalah koordinat silinder dan sfera yang diselesaikan. Pulih dari: pengiraan.DC
3. Weisstein, Eric W. "Koordinat silinder."Dari Mathworld-A Wolfram Web. Pulih dari: Mathworld.Wolfram.com
4. Wikipedia. Sistem koordinat silinder. Diperoleh dari: dalam.Wikipedia.com
5. Wikipedia. Medan vektor dalam koordinat silinder dan sfera. Diperoleh dari: dalam.Wikipedia.com