Fungsi dan aplikasi trigonometri bulatan kesatuan

Dia Lingkaran kesatuan Ia adalah lingkaran radius sama dengan 1, yang biasanya difokuskan pada titik (0.0) sistem koordinat Cartesian Xy. Ia digunakan untuk dengan mudah menentukan sebab -sebab trigonometri sudut dengan segi empat tepat.

Persamaan lingkaran kesatuan yang difokuskan pada asal adalah:

x² + dan² = 1

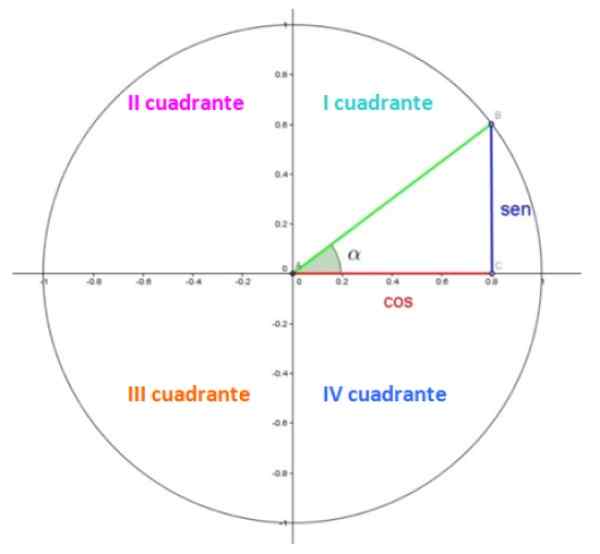
Rajah 1. Lingkaran unit. Sumber: Wikimedia Commons.

Dalam Rajah 1 kita mempunyai lingkaran unit, di mana setiap bilik berada dalam kuadran. Kuadran dihitung dengan nombor Rom dan dikira anti -horary.

Di kuadran pertama terdapat segitiga. Kategori, merah dan dalam ukuran biru masing -masing 0.8 dan 0.6, manakala Hypotenuse dalam Langkah Hijau 1, kerana ia adalah radio.

Sudut akut α adalah sudut pusat dalam kedudukan standard, yang bermaksud bahawa puncaknya bertepatan dengan titik (0.0) dan bahagian awalnya dengan paksi x positif. Sudut diukur bertentangan dengan tangan jam dan dengan konvensyen ia diberikan tanda positif.

Nah, dalam lingkaran unit, koordinat coseno dan sinus α masing -masing adalah koordinat x dan y titik b, yang dalam contoh yang ditunjukkan adalah 0.8 dan 0.6.

Dari kedua -dua mereka ditakrifkan:

• Tg α = sin α/cos α = 0.6/0.8 = 0.75
• Sec α = 1/ cos α = 1/0.8 = 1.25
• bahaya α = 1 / sin α = 1/0.6 = 1.66 ..
• CTG α = 1/TG = 0.8/0.6 = 1.33 ..

[TOC]

Aplikasi Circle Union

Sekiranya kita mengehadkan diri kita kepada segi empat tepat, alasan trigonometri hanya akan digunakan untuk sudut akut. Walau bagaimanapun, dengan bantuan lingkaran unit, pengiraan sebab -sebab trigonometrik dilanjutkan kepada mana -mana sudut α.

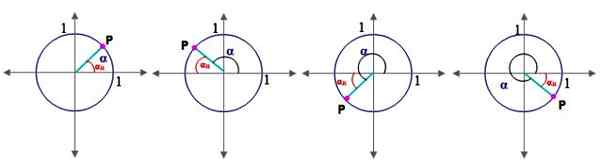
Rajah 2.- Sudut di kuadran dan sudut rujukan dalam lingkaran unit. Sumber: f. Zapata.

Untuk ini, perlu menentukan konsep sudut rujukan α pertama_R:

Boleh melayani anda: set terhingga: sifat, contoh, latihan yang diselesaikan

Sudut rujukan

Biarkan α menjadi sudut dalam kedudukan standard (yang mana Bahagian awal bertepatan dengan paksi x positif), sudut rujukannya α_R Ia adalah antara yang sisi terminal dan paksi x. Rajah 2 menunjukkan sudut rujukan untuk sudut dalam kuadran I, II, III dan IV.

Bagi setiap kuadran, sudut rujukan dikira seperti berikut:

-Kuadran Pertama: α_R = α

-Kuadran kedua: α_R = 180º - α

-Kuadran ketiga: α_R = α - 180º

-Kuadran Keempat: α_R = 360º - α

Perhatikan bahawa sudut kuadran pertama α bertepatan dengan sudut rujukannya. Nah, alasan trigonometri untuk sudut α adalah sama dengan sudut rujukan mereka, dengan tanda -tanda menurut mereka yang mempunyai kuadran di mana sisi terminal α jatuh.

Dalam erti kata lain, sebab -sebab trigonometri coseno dan payudara sudut α bertepatan dengan koordinat titik p, menurut Rajah 2.

Dalam angka berikut, kita melihat sebab -sebab trigonometri beberapa sudut yang ketara, seperti yang disimpulkan dari lingkaran unit.

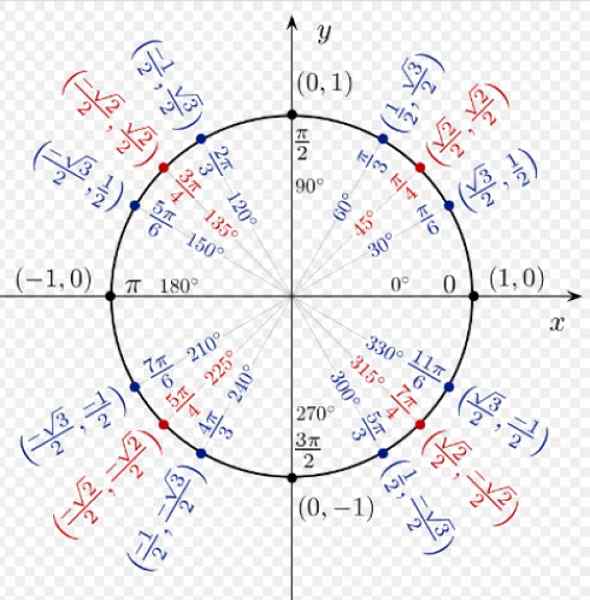Rajah 3. Menyelaras beberapa titik penting dalam lingkaran unit. Sumber: Wikimedia Commons.

Sebab Coseno dan payudara dari mana -mana sudut di kuadran I semuanya positif. Untuk α = 60º kita mempunyai koordinat (1/2; √3/2), yang sesuai dengan COS 60º dan SEN 60º.

Koordinat α = 120º adalah (-1/2; √3/2), kerana berada di kuadran kedua, koordinat x adalah negatif.

Susun atur graf kosin dan sinus

Dengan bantuan lingkaran unit dan koordinat titik P di atasnya, adalah mungkin untuk menarik graf fungsi cos t dan sen t, seperti yang akan kita lihat di bawah.

Boleh melayani anda: anjakan sudut

Untuk ini, beberapa kedudukan titik p (t) terletak di lingkaran unit. Kita akan mulakan dengan graf fungsi f (t) = sen t.

Kita dapat melihat bahawa apabila kita pergi dari t = 0 hingga t = π/2 (90º) nilai sen t meningkat kepada 1, iaitu nilai maksimum.

Sebaliknya, dari t = π/2 hingga t = 3π/2 nilai sin t menurun dari 1, melalui 0 pada t = π hingga minimum -1 pada t = 3π/2.

Angka ini menunjukkan graf kitaran pertama f (t) = sen t yang sepadan dengan pulangan pertama ke lingkaran unit, fungsi ini adalah tempoh berkala 2π.

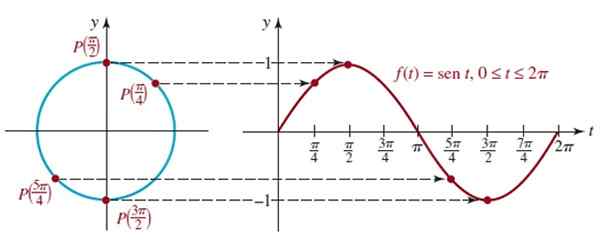Rajah 4. Angka graf f (t) = sen t untuk kitaran. Sumber: Zill, D. Algebra, trigonometri dan geometri analisis.

Prosedur analog boleh dijalankan untuk mendapatkan graf fungsi f (t) = cos t, seperti yang ditunjukkan dalam animasi berikut:

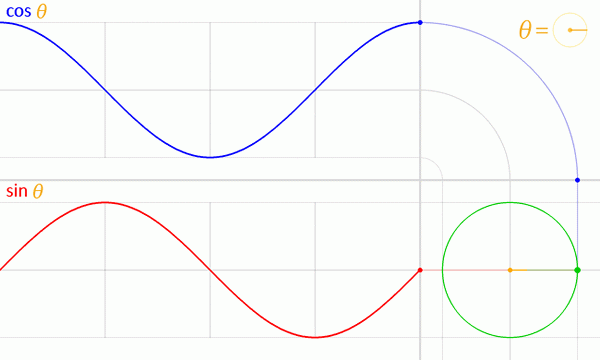Rajah 5. Grafik fungsi sinus dan kosinus dari lingkaran unit. Sumber: Wikimedia Commons.

Sifat fungsi Seno dan Coseno

-Kedua -dua fungsi berterusan dalam set nombor sebenar dan juga berkala, tempoh 2π.

-Domain fungsi f (t) = sen t dan f (t) = cos t adalah semua nombor sebenar: (-∞, ∞).

-Untuk laluan payudara atau sinus dan kosinus, anda mempunyai selang [-1,1]. Kurungan menunjukkan bahawa -1 dan 1 dimasukkan.

- Zeros dosa adalah nilai -nilai yang sesuai dengan nπ dengan integer n, manakala sifar cos t adalah [(2n+1)/2] dengan n juga keseluruhan.

-Fungsi f (t) = sin t adalah ganjil, mempunyai simetri berkenaan dengan asal manakala fungsi kos t adalah, simetrinya adalah berkenaan dengan paksi menegak.

Boleh melayani anda: pilihan rawak dengan atau tanpa penggantian

Latihan yang diselesaikan

- Latihan 1

Diberikan cos t = - 2/5, yang merupakan koordinat mendatar titik p (t) dalam lingkaran unit dalam kuadran kedua, mendapatkan koordinat menegak yang sepadan.

Penyelesaian

Oleh kerana p (t) tergolong dalam lingkaran unit, di mana ia dipenuhi bahawa:

x² + dan² = 1

Oleh itu:

y = ± √ 1 - x²

Oleh kerana p (t) berada di kuadran kedua nilai positif akan diambil. Koordinat menegak titik p (t) adalah y:

y = √ 1 - (-2/5)² = √0.84

- Latihan 2

Model matematik untuk suhu T Dalam darjah Fahrenheit pada bila -bila masa, t Jam selepas tengah malam, ia diberikan oleh:

T (t) = 50 + 10 sen [(π /12) × (t - 8)]

Dengan T difahami antara 0 dan 24 jam. Cari:

a) suhu pada pukul 8 pagi.

b) jam di mana t (t) = 60 ºF

c) suhu maksimum dan minimum.

Penyelesaian kepada

Kami menggantikan t = 8 dalam fungsi yang diberikan:

T (8) = 50 + 10 sen [(π/12) × (t-8)] = 50 + 10 sen [(π/12) × (8-8)] =

= 50 + 10 x sen 0 = 50 ºF

Penyelesaian b

50 + 10 sen [(π/12) × (t-8)] = 60

Ia adalah persamaan trigonometri dan anda perlu membersihkan "t" yang tidak diketahui:

10 sen [(π/12) × (t -8)] = 60 - 50 = 10

dosa [(π/12) × (t-8)] = 1

Kita tahu bahawa sen π/2 = 1, oleh itu hujah payudara harus 1:

(π/12) × (t-8) = π/2

T-8 = 6

t = 14 jam

Disimpulkan bahawa 14 jam selepas tengah malam suhu adalah 60 °, iaitu 2 petang. Tidak ada jam lain sepanjang hari (24 jam) di mana ini berlaku.

Penyelesaian c

Suhu maksimum sepadan dengan nilai di mana sen [(π/12) × (t-8)] = 1 dan adalah 60 ºF. Sebaliknya, minimum berlaku jika sen [(π/12) × (t -8)] = -1 dan 40 ºF.

Rujukan

1. Figuera, j. 1999. Matematik. 1st. Dipelbagaikan. Edisi Bolivarian Collegiate.
2. Hoffman, J. Pemilihan masalah matematik. Jilid 4.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Matematik menyeronokkan. Bulatan Unit. Pulih dari: Dari: MathSisfun.com.
5. Wikipedia. Identiti dan formula trigonometri. Pulih dari: Adakah.Wikipedia.org.
6. Zill, d. 1984. Algebra dan trigonometri. McGraw Hill.