Identiti trigonometri (contoh dan latihan)

The identiti trigonometri Ini adalah hubungan antara sebab -sebab trigonometri, yang benar untuk sebarang nilai pembolehubah. Sebagai contoh:

Tan θ = sin θ /cos θ

Ini adalah identiti trigonometri yang mengaitkan tiga sebab sudut θ, tangen, payudara dan kosinus sudut tersebut.

Rajah 1. Beberapa identiti trigonometri digunakan secara meluas dalam pengiraan. Sumber: f. Zapata.

Identiti ini benar untuk semua nilai, kecuali yang menjadikan 0 penyebut. Cos θ ialah 0 untuk θ = ± π/2, ± 3π/2, ± 5π/2 ... Satu lagi contoh identiti trigonometri ialah:

dosa x . Sec x . Ctg x = 1

[TOC]

Demonstrasi

Terdapat dua cara asas untuk menunjukkan bahawa identiti trigonometri adalah benar:

1- Mengubah salah satu ahli kesamaan ke yang lain, melalui manipulasi algebra yang mudah.

2- Membangunkan kedua-dua ahli kesamaan secara berasingan, sehingga ungkapan akhir masing-masing adalah sama persis.

Dalam identiti yang dicadangkan, kita akan mengubah sisi kiri kesamaan, yang mana kita menyatakan CTG X dan Sec X dari segi payudara dan kosinus seperti berikut:

Ctg x = cos x / sen x

Sec x = 1 /cos x

Kami menggantikan ungkapan ini di sebelah kiri identiti dan memudahkan:

dosa x . (1/cos x). (cos x / sen x) = (sin x. cos x / cos x . dosa x) = 1

Dan kebenaran identiti sudah terbukti.

Jenis identiti trigonometri

Terdapat beberapa jenis identiti trigonometri. Seterusnya kita akan menerangkan secara ringkas yang utama:

- Identiti trigonometri asas

Kami membezakan dua jenis identiti asas:

I) Mereka yang dinyatakan melalui sebab -sebab asas, kosinus dan tangen:

• Sec x = 1 /cos x
• Bahaya x / 1 / sin x
• Ctg x = 1 / tg x
• Tg x = sin x /cos x
• Ctg x = cos x / sen x

I) yang berasal dari pariti. Kita tahu melalui grafnya bahawa Sen x adalah fungsi ganjil, yang bermaksud:

Boleh melayani anda: 60 pembahagi

dosa (-x) = - dosa x

Bagi bahagiannya cos x adalah pasangan, oleh itu:

cos (-x) = cos x

Jadi:

Tg (-x) = sen (-x) / cos (-x) = -sen x / cos x

Begitu juga:

• cotg (-x) = -ctg x
• sec (-x) = sec x
• kemudaratan (-x) = - bahaya x

- Identiti Pythagorean

Mereka adalah yang diperolehi dari penggunaan teorem Pythagoras ke segi empat tepat kucing A dan B dan Hypotenusa C. Mari kita lihat:

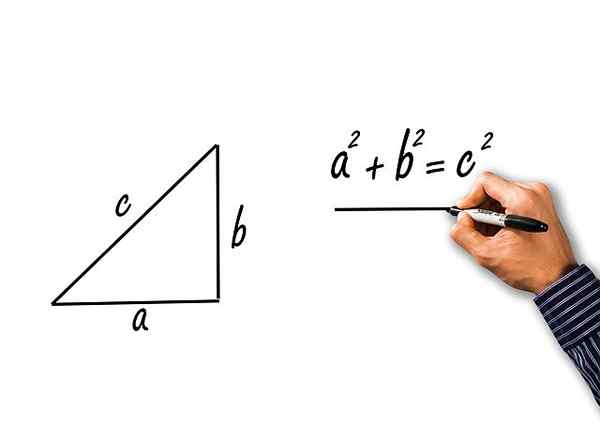Rajah 2.- Dari teorem Pythagoras, tiga identiti trigonometri Pythagorean diperoleh. Sumber: Pixabay.

Teorem Pythagoras menyatakan bahawa:

c² = a² + b²

Membahagikan segala -galanya antara c²:

c² / c² = (a² / c²) + (B² / c²)

Istilah di sebelah kiri adalah 1 dan mengingati bahawa sinus dan kosinus sudut akut α ditakrifkan sebagai:

sin α = a/c

cos α = b/c

Hasilnya:

1 = (sin α)² + (cos α)²

Identiti ini dikenali sebagai identiti asas.

Prosedur ini boleh dijalankan dengan membahagikan antara² dan b², yang menimbulkan dua lagi identiti:

Sec² α = 1 + tg² α

HAR² α = 1 + ctg² α

- Formula untuk kosinus dan payudara jumlah/penolakan sudut

Identiti trigonometri utama untuk kosinus, payudara dan tangen jumlah dan penolakan adalah berikut:

Demonstrasi SEN (α + β) dan COS (α + β)

Identiti ini boleh ditunjukkan secara geometri atau juga melalui formula Euler:

dan^Iα = cos α + saya berdosa α

Mari kita lihat apa yang berlaku kepada formula apabila menggantikan jumlah dua sudut α dan β:

dan^{I (α +β)} = cos (α + β) + I Sin (α + β)

Ekspresi ini rumit, bahagian sebenar adalah COS (α + β) dan bahagian khayalannya adalah saya dosa (α + β). Kami mengekalkan hasil ini untuk menggunakannya kemudian dan memberi tumpuan kepada membangunkan bahagian eksponen:

dan^{I (α +β)} = e^Iα ⋅ e^Iβ = (cos α + i sin α) . (cos β + i sin β) =

Boleh melayani anda: prisma heksagon

= COS α ⋅ cos β + cos α sen β + i α α cos β - sen α αss β β

Bahagian sebenar ungkapan ini adalah yang tidak didarabkan oleh unit khayalan "I":

cos α ⋅ cos β - sen α. Sen β

Oleh itu, bahagian khayalan adalah:

I (cos α αSEN β + SEN α ​​αCOS β)

Untuk dua ungkapan kompleks yang sama, bahagian sebenar seseorang mestilah sama dengan bahagian sebenar yang lain. Perkara yang sama berlaku untuk bahagian khayalan.

Kami mengambil hasil yang disimpan dan membandingkannya dengan ini:

cos α. cos β - sen α. sin β = cos (α + β)

I (cos α αSEN β + SEN α ​​αCOS β) = I Sin (α + β)

dosa (α + β) = (cos α. sin β + sen α αcos β)

- Formula untuk sudut berganda

Dalam formula sebelumnya kita ambil β = α dan berkembang:

sin (α + α) = sen 2 α = sen α α α + cos α. sin α = 2 ⋅ sin α ⋅ cos α

cos (α + α) = cos 2 α = cos α αcos α - sen α α α α = cos² α - sen ² α

Tg (α + α) = Tg 2 α = [Tg α + Tg α] / [1- Tg α α α] = 2Tg α / 1- Tg² α

Sekiranya dalam ekspresi kedua cos diganti² α = 1 - sen² α diperoleh:

cos 2 α = cos² α- (1- cos² α) = 2 cos² α -1

- Formula separuh -sudut

Dalam ungkapan terakhir ini kita menggantikan α dengan α/2, yang berikut tetap:

cos α = 2 cos ²(α/2) -1

Membersihkan:

Latihan yang diselesaikan

- Latihan 1

Tunjukkan bahawa:

Penyelesaian

Kita akan bekerja secara algebra secara istilah yang tersisa sehingga kelihatan seperti betul. Seperti dalam istilah yang betul muncul sen x, langkah pertama adalah untuk menyatakan kos²X Dari segi Sen x supaya segala -galanya adalah dari segi alasan trigonometri yang sama:

Ia boleh melayani anda: pecahan bersamaan dengan 3/5 (penyelesaian dan penjelasan)

Kemudian 1 - Sen adalah faktor² x Untuk menjadi perbezaan dataran yang sempurna. Untuk melakukan ini, ia membersihkan dari identiti asas:

cos²X = 1 - Sen² x

1 - Sen² x = (1- sin x) (1+senx)

Dan pemfaktoran dalam ungkapan asal diganti:

Istilah (1- senx) dipermudahkan dan kesamaan kekal:

1 + sen x = 1 + senx

- Latihan 2

Selesaikan persamaan trigonometri berikut dan berikan penyelesaian untuk nilai antara 0 dan 360º:

Tg x + sec² x = 3

Penyelesaian

Dalam tempoh kiri terdapat dua sebab trigonometri, oleh itu anda perlu mengurangkan segala -galanya kepada satu, untuk dapat membersihkan yang tidak diketahui. Istilah sec² X dinyatakan melalui salah satu identiti Pythagorean:

Sec² α = 1 + tg² α

Dengan menggantikan persamaan:

Tg x + 1 + tg² x = 3

Menyusun semula syarat:

Tg² x + tg x + 1 = 3

Persamaan ini diselesaikan dengan menukar pembolehubah:

tg x = u

atau² + U + 1 - 3 = 0 → u² + U - 2 = 0

Persamaan ijazah kedua ini mudah diselesaikan dengan pemfaktoran:

(U +2) (u-1) = 0

Oleh itu u₁ = -2 dan u₂ = 1, bersamaan dengan:

Tg x₁ = -2

Tg x₂ = 1

Akhirnya:

x₁ = arctg (-2) = 296.6th

x₂  = arctg (1) = 45º

Rujukan

1. Carena, m. 2019. Manual Matematik PraUniversiti. Universiti Kebangsaan Pantai.
2. Figuera, j. 1999. Matematik. 1st. Dipelbagaikan. Edisi Bolivarian Collegiate.
3. Hoffman, J. Pemilihan masalah matematik. Jilid 4.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Wikipedia. Identiti dan formula trigonometri. Pulih dari: Adakah.Wikipedia.org.
6. Zapata, f. 4 cara untuk menyelesaikan persamaan darjah kedua. Pulih dari: Francesphysics.Blogspot.com.
7. Zill, d. 1984. Algebra dan trigonometri. McGraw Hill.