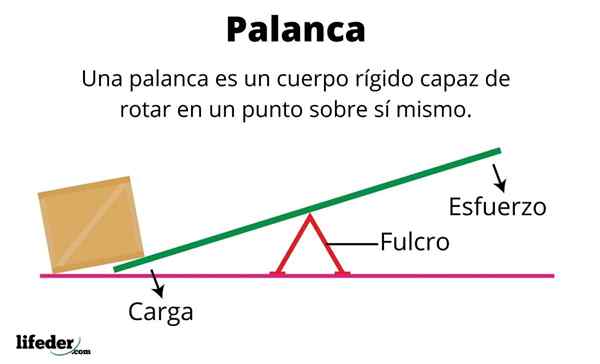
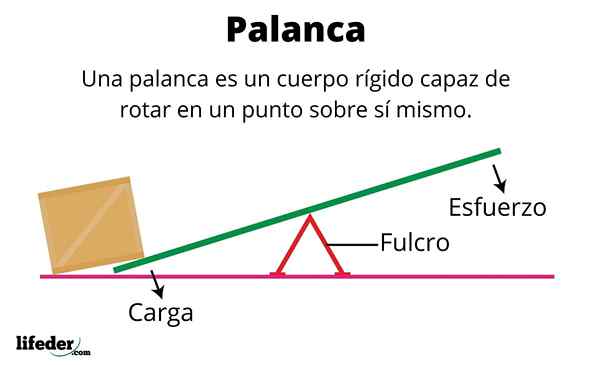
Jasad tegar

Apa itu badan yang tegar?

Badan tegar adalah objek material yang zarahnya selalu berada di kedudukan relatif yang sama. Oleh itu ia adalah objek yang tidak cacat, kualiti yang dikaitkan dengan daya perpaduan yang sengit yang memelihara zarah di tempatnya.

Sebenarnya zarah -zarah dari mana -mana badan yang tertakluk kepada daya luaran cenderung bergetar atau bergerak, jadi objek selalu berubah sedikit pun, tetapi kesan ini biasanya kecil.

Apabila ini berlaku, dapat diandaikan bahawa badan itu tegar dan mempunyai pendekatan yang sangat baik terhadap tingkah lakunya, walaupun ia adalah idealisasi.

Jenis badan yang tegar

Anda boleh membezakan dua jenis badan tegar:

• Mereka yang zarahnya datang dalam kuantiti diskret, iaitu, mereka boleh mengira. Sebagai contoh, dua sfera logam yang dikaitkan dengan batang nipis dan ringan boleh dianggap sebagai entiti yang unik. Sekiranya batangnya cukup tegar untuk tidak bengkok, sistem dianggap sebagai badan yang tegar.
• Mereka yang berterusan, yang bermaksud bahawa zarah -zarah yang membuatnya tidak dapat dibezakan. Objek setiap hari dan alam adalah contoh yang baik: batu, perabot dan lain -lain, serta tanah dan batu langit yang lain berbatu.

Pergerakan dan Dinamik Badan Kekal

Seperti objek yang dianggap sebagai zarah, badan tegar boleh dipindahkan, berputar dan mempunyai pergerakan yang lebih umum, menggabungkan terjemahan dan putaran.

Untuk mengkaji terjemahan itu tidak perlu.

Pergerakan terjemahan dan putaran ini boleh:

• Bebas, seperti dalam hal planet, yang mempunyai pergerakan putaran di sekitar paksi mereka (dianggap tetap) dan satu lagi terjemahan di sekitar matahari, tetapi kelajuan masing -masing tidak berkaitan.
• Rosak-jejak, jika halaju sudut dan kelajuan terjemahan pusat jisim berkaitan. Dalam kes ini, paksi putaran adalah mudah alih, seperti dalam hal silinder yang turun menembak tanpa tergelincir oleh lereng cenderung.

Ia boleh melayani anda: Undang -undang Termodinamik Pertama: Formula, Persamaan, Contoh

Dinamik pepejal tegar

Magnitud berikut adalah relevan dalam dinamik pepejal tegar:

Pusat Massa

Pusat jisim adalah titik di mana seluruh jisim badan dianggap tertumpu. Sekiranya ia adalah badan yang homogen dan simetri, sebagai sfera, pusat jisim bertepatan dengan pusat geometri.

Saat inersia

Magnitud skalar ini adalah nilai inersia putaran atau rintangan yang menentang objek untuk berputar di sekitar paksi tertentu. Ia bergantung sepenuhnya pada geometri objek dan jisimnya dan oleh itu, dalam kes -kes tertentu, lebih mudah untuk menghidupkan paksi tertentu daripada yang lain.

Untuk badan -badan dengan bentuk geometri yang ditentukan dengan baik, terdapat jadual dengan momen inersia berkenaan dengan paksi simetri, contohnya yang melewati pusat massa. Dengan maklumat ini dan teorem yang berkaitan dengan momen inersia, detik -detik berkenaan dengan paksi lain dapat dikira dengan mudah.

Daya dan tork atau tork

Kuasa dikehendaki menggerakkan badan. Sekiranya pusat jisim pepejal tegar bergerak, persamaan pergerakan, menurut undang -undang kedua Newton, adalah:

F_Jaring = M ∙ke_cm

Di mana:

-Kekuatan bersih adalah F_Jaring

-M adalah jisim

-Pecutan pusat jisim adalah ke_cm

Walau bagaimanapun, tidak semua kuasa yang digunakan membuat objek berehat. Untuk melakukan ini, tork atau tork diperlukan, yang mengatakan betapa berkesannya tindakan putaran daya. Ia ditakrifkan sebagai produk vektor antara vektor kedudukan r Mengenai titik dan kekuatan tertentu F dalam soalan. Ia dilambangkan oleh surat Yunani τ (Dalam huruf tebal, ia juga vektor):

Boleh melayani anda: pergerakan elips

τ = r × F

Dalam sistem antarabangsa, unit tork adalah n (Newton per meter).

Dalam banyak kes, pergerakan putaran di sekitar paksi yang melewati pusat jisim digambarkan oleh persamaan analog dengan undang -undang kedua Newton:

Di mana subskrip "z" merujuk kepada paksi putaran yang melalui paksi simetri, tetap atau bergerak, tetapi tanpa mengubah arah, dan_cm Ia adalah momen inersia berkenaan dengan pusat jisim dan α_z Ia adalah pecutan sudut badan. Musim panas merangkumi semua momen luaran di sekitar paksi z.

Tenaga kinetik pepejal tegar

Pergerakan badan tegar digambarkan oleh terjemahan pusat jisim dan putaran sekitar titik itu, oleh itu, tenaga kinetiknya mempunyai kedua -dua sumbangan.

Biarkan K Tenaga Kinetik Badan, V_cm Kelajuan pusat jisim, j jisim badan, dan_cm momen inersia berkenaan dengan pusat jisim dan Ω halaju sudut. Ia boleh ditunjukkan bahawa tenaga kinetik adalah:

K = ½ mV_cm² + ½ i_cm Ω²

Diperhatikan bahawa istilah kedua di sebelah kanan adalah analog putaran istilah kiri. Di sana momen inersia memainkan peranan yang sama dengan jisim, sementara halaju sudut mempunyai peranan yang sama dengan kelajuan linear.

Contoh dalam kehidupan seharian

Pendulum fizikal

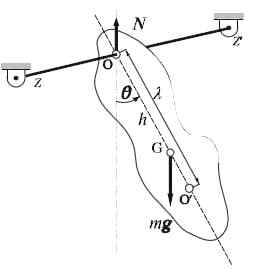Pendulum fizikal

Pendulum fizikal atau pendulum sebenar sangat mudah dibina: ia terdiri daripada pepejal tegar seperti batang atau bar, berayun secara bebas di sekitar paksi mendatar. Paksi putaran tidak menyeberangi pusat jisim objek dan ini pada dasarnya boleh mempunyai bentuk.

Boleh melayani anda: termometer rintangan: ciri, operasi, kegunaan

Pendulum ini berbeza dari pendulum sederhana, kerana di dalamnya, ia dianggap bahawa jisim yang membentuknya adalah tepat waktu.

Roda basikal

Roda basikal

Satu lagi contoh badan tegar yang terkenal ialah roda basikal, yang paksi melewati pusat jisim, yang melintasi pusat roda. Selagi mereka tidak bersandar pada sisi atau giliran, persamaan dinamik yang diterangkan berlaku untuk menggambarkan pergerakan anda.

Bola boling

Contoh yang baik dari badan yang tegar adalah bola boling

Model pepejal tegar menyesuaikan diri dengan sangat baik untuk menggambarkan pergerakan bola boling di trek atau ketika ia menggulung tanpa meluncur ke jalan balik.

Yoyo

Yoyo adalah mainan popular yang boleh dimodelkan seperti badan yang tegar

Mainan popular ini dibuat dengan silinder kayu atau plastik dan tali yang dibebani dalam slot yang mengelilinginya.

Silinder boleh dimodelkan sebagai badan tegar di mana voltan dalam rentet.

Rujukan

1. Bauer, w. 2011. Fizik untuk Kejuruteraan dan Sains. Jilid 1. MC Graw Hill. 
2. Giancoli, d.  2006. Fizik: Prinsip dengan aplikasi. 6th. Ed Prentice Hall.
3.  Katz, d. 2013. Fizik untuk saintis dan jurutera. Asas dan sambungan. Pembelajaran Cengage.
4. Sears, Zemansky. 2016. Fizik universiti dengan fizik moden. Ke -14. Ed. Jilid 1. Pearson.
5. Serway, r., Jewett, J. (2008). Fizik untuk Sains dan Kejuruteraan. Jilid 1. Ke -7. Ed. Pembelajaran Cengage.