Berapa banyak penyelesaian yang dimiliki oleh persamaan kuadratik?

Persamaan kuadratik atau persamaan darjah kedua boleh mempunyai sifar, satu atau dua penyelesaian sebenar, bergantung kepada pekali yang muncul dalam persamaan tersebut. Jika anda bekerja pada nombor kompleks, maka anda boleh mengatakan bahawa setiap persamaan kuadratik mempunyai dua penyelesaian.

Untuk memulakan persamaan kuadratik, ia adalah persamaan bentuk kapak+bx+c = 0, di mana a, b dan c adalah nombor sebenar dan x adalah pembolehubah.

Dikatakan bahawa x1 adalah penyelesaian persamaan kuadratik sebelumnya jika apabila menggantikan x oleh x1 persamaan dipenuhi, iaitu, jika a (x1) ²+b (x1)+c = 0.

Jika anda mempunyai contoh persamaan x²-4x+4 = 0, maka x1 = 2 adalah penyelesaian, kerana (2) ² (2) +4 = 4-8+4 = 0.

Sebaliknya, jika x2 = 0 diganti, ia diperoleh (0) ²-4 (0) +4 = 4 dan sebagai 4 ≠ 0 maka x2 = 0 bukan penyelesaian persamaan kuadrat.

Penyelesaian persamaan kuadrat

Bilangan penyelesaian persamaan kuadrat boleh dipisahkan dalam dua kes yang:

1.- Dalam nombor sebenar

Apabila bekerja dengan nombor sebenar, persamaan kuadrat boleh mempunyai:

-Penyelesaian Zero: iaitu, tidak ada nombor sebenar yang memenuhi persamaan kuadrat. Sebagai contoh, persamaan yang diberikan x²+1 = 0, tidak ada bilangan sebenar yang memenuhi persamaan tersebut, kerana kedua -dua x² lebih besar daripada atau sama dengan sifar dan 1 adalah lebih ketat daripada sifar, sehingga jumlahnya lebih besar Ketat daripada sifar.

-Penyelesaian berulang: Terdapat satu nilai sebenar yang memenuhi persamaan kuadrat. Sebagai contoh, satu-satunya penyelesaian persamaan x²-4x+4 = 0 ialah x1 = 2.

-Dua penyelesaian yang berbeza: Terdapat dua nilai yang memenuhi persamaan kuadrat. Contohnya, x²+x -2 = 0 mempunyai dua penyelesaian yang berbeza iaitu x1 = 1 dan x2 = -2.

2.- Dalam nombor kompleks

Semasa bekerja dengan nombor kompleks, persamaan kuadratik selalu mempunyai dua penyelesaian, iaitu Z1 dan Z2 di mana Z2 adalah konjugasi Z1. Di samping itu, mereka boleh diklasifikasikan sebagai:

-Kompleks: Penyelesaiannya adalah bentuk z = p ± qi, di mana p dan q adalah nombor sebenar. Kes ini sepadan dengan kes pertama senarai sebelumnya.

-Kompleks tulen: Ia adalah apabila bahagian sebenar penyelesaiannya sama dengan sifar, iaitu penyelesaiannya mempunyai bentuk z = ± qi, di mana q adalah nombor sebenar. Kes ini sepadan dengan kes pertama senarai sebelumnya.

-Kompleks dengan bahagian khayalan sama dengan sifar: Ia adalah ketika bahagian kompleks penyelesaiannya sama dengan sifar, iaitu penyelesaiannya adalah bilangan sebenar. Kes ini sepadan dengan dua kes terakhir senarai sebelumnya.

Bagaimana penyelesaian persamaan kuadrat dikira?

Untuk mengira penyelesaian persamaan kuadrat, formula yang dikenali sebagai "resolusi" digunakan, yang mengatakan bahawa penyelesaian AX ²+bx+c = 0 persamaan diberikan oleh ungkapan imej berikut:

Jumlah yang muncul dalam akar kuadrat dipanggil diskriminasi persamaan kuadrat dan dilambangkan oleh huruf "d".

Persamaan kuadrat akan mempunyai:

-Dua penyelesaian sebenar ya, dan hanya ya, d> 0.

-Penyelesaian sebenar berulang jika, dan hanya jika, d = 0.

-Penyelesaian sifar sebenar (atau dua penyelesaian kompleks) ya, dan hanya ya, d<0.

Contoh

-Penyelesaian persamaan x²+x-2 = 0 diberikan oleh:

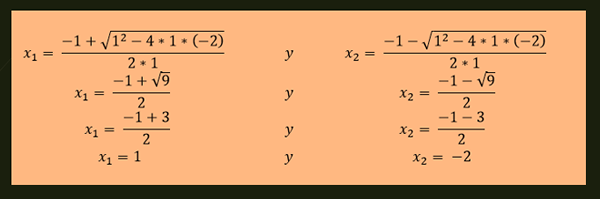
-Persamaan x²-4x+4 = 0 mempunyai penyelesaian berulang yang diberikan oleh:

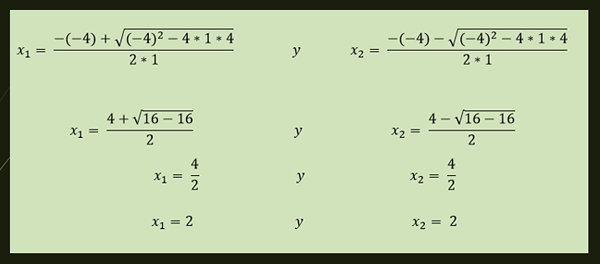
-Penyelesaian persamaan x²+1 = 0 diberikan oleh:

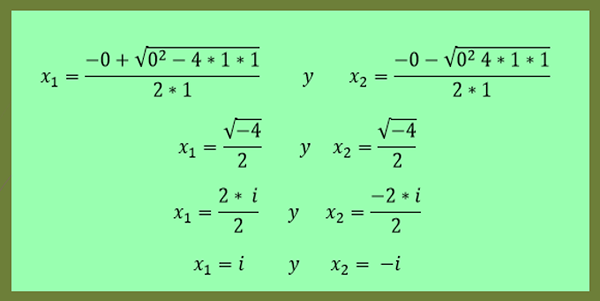
Seperti yang dapat dilihat dalam contoh terakhir ini, x2 adalah konjugasi x1.