Definisi, jenis, formula, apa itu, contohnya,

The Curtosis atau kurtosis Ia adalah parameter statistik yang berfungsi untuk mencirikan taburan kebarangkalian pemboleh ubah rawak, yang menunjukkan tahap kepekatan nilai di sekitar ukuran pusat. Ini juga dikenali sebagai "gred puncak".

Istilah ini berasal dari "kurtos" Yunani yang bermaksud melengkung, oleh itu curtosis menunjukkan tahap penunjuk atau meratakan pengedaran, seperti yang dilihat dalam angka berikut:

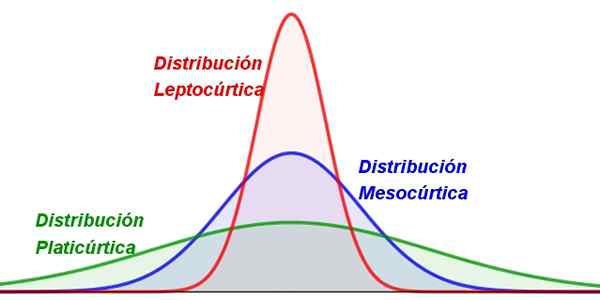Rajah 1. Pelbagai jenis curtosis. Sumber: f. Zapata.

Hampir semua nilai pemboleh ubah rawak cenderung untuk berkumpul di sekitar nilai pusat seperti purata. Tetapi dalam beberapa pengagihan, nilai -nilai itu lebih tersebar daripada yang lain, mengakibatkan keluk yang lebih rata atau lebih langsing.

[TOC]

Definisi

Curtosis adalah nilai berangka setiap pengagihan kekerapan, yang menurut kepekatan nilai sekitar purata, diklasifikasikan kepada tiga kumpulan:

-Leptocuric: di mana nilai -nilai sangat dikumpulkan sekitar purata, jadi pengedarannya agak tajam dan langsing, (Rajah 1, kiri).

-Mesocuric: Ia mempunyai kepekatan nilai sederhana sekitar purata (Rajah 1 di tengah).

-Phylicuric: Pengagihan ini mempunyai bentuk yang lebih luas, kerana nilai -nilai cenderung lebih bertaburan (Rajah 1 ke kanan).

Formula dan persamaan

Curtosis boleh mempunyai nilai, tanpa batasan. Pengiraannya dijalankan bergantung pada cara data yang disampaikan. Notasi yang digunakan dalam setiap kes adalah seperti berikut:

-Koefisien Cortosis: g₂

-Purata aritmetik: X atau x dengan bar

-I-eme: x_Yo

-Sisihan piawai: σ

-Bilangan data: N

-Kekerapan i-esimo: F_Yo

-Jenama Kelas: mx_Yo

Dengan notasi ini, kami membentangkan beberapa formula yang paling biasa digunakan untuk mencari curtosis:

Boleh melayani anda: ruang vektor: asas dan dimensi, aksioma, sifat

- Curtosis mengikut pembentangan data

Tanpa kumpulan kumpulan atau dikumpulkan pada frekuensi

Data dikumpulkan pada selang waktu

Lebihan curtosis

Juga dipanggil Koefisien menunjuk Fisher Sama ada Ukuran Fisher, Ia berfungsi untuk membandingkan pengedaran yang sedang dikaji dengan pengedaran normal.

Apabila curtosis berlebihan bernilai 0, kita berada di hadapan taburan normal atau loceng gauss. Dengan cara ini, selagi penyamakan kelebihan pengedaran dikira, kita sebenarnya membandingkannya dengan taburan normal.

Kedua -duanya untuk data tanpa kumpulan dan untuk data yang dikumpulkan, pekali penunjuk Fisher, yang dilambangkan oleh k, adalah:

K = g₂ - 3

Walau bagaimanapun, ia dapat ditunjukkan bahawa curtosis pengedaran normal adalah 3, oleh itu jika pekali penunjuk nelayan adalah 0 atau hampir 0 dan terdapat pengedaran mesokurik. Jika k> 0 pengedaran adalah leptokurik dan jika k<0 es platicúrtica.

Apa itu curtosis untuk?

Curtosis adalah ukuran kebolehubahan yang digunakan untuk mencirikan morfologi pengedaran. Dengan cara ini, pengagihan simetri dapat dibandingkan dengan penyebaran purata dan sama yang sama (diberikan oleh sisihan piawai).

Mempunyai langkah -langkah kebolehubahan memastikan purata boleh dipercayai dan membantu mengawal variasi pengedaran. Sebagai contoh, mari kita menganalisis kedua -dua situasi ini.

3 jabatan gaji

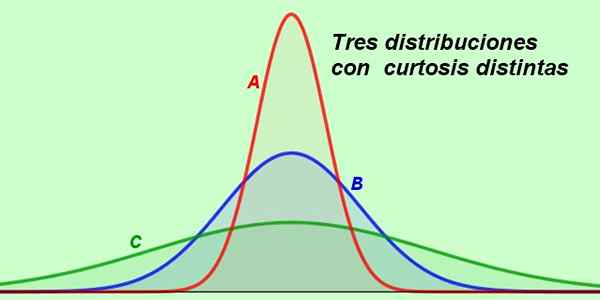
Katakan graf berikut menunjukkan pengagihan dalam gaji 3 jabatan syarikat yang sama:

Rajah 2. Tiga pengagihan yang berbeza menggambarkan situasi praktikal. (Disediakan oleh Fanny Zapata)

Curve A adalah yang paling langsing dari semua, dan dalam bentuknya disimpulkan bahawa kebanyakan gaji jabatan itu sangat dekat dengan purata, oleh itu kebanyakan pekerja menerima pampasan yang sama.

Boleh melayani anda: keseluruhan nombor

Bagi bahagiannya di Jabatan B, lengkung gaji mengikuti taburan normal, kerana lengkungnya adalah mesocuric, di mana kita mengandaikan bahawa gaji telah diedarkan secara rawak.

Dan akhirnya kita mempunyai lengkung c yang sangat diratakan, tanda bahawa di jabatan ini julat gaji jauh lebih luas daripada yang lain.

Hasil peperiksaan

Katakan sekarang bahawa tiga lengkung Rajah 2 mewakili hasil peperiksaan yang digunakan untuk tiga kumpulan pelajar yang sama subjek.

Kumpulan yang kelayakannya diwakili oleh lengkung ke leptokurik, agak homogen, kebanyakannya memperoleh penarafan purata atau dekat.

Ia juga mungkin bahawa hasilnya disebabkan oleh fakta bahawa soalan peperiksaan mempunyai tahap kesukaran yang sama.

Sebaliknya, hasil Kumpulan C menunjukkan heterogeniti yang lebih besar dalam kumpulan, yang mungkin mengandungi pelajar purata, beberapa pelajar yang lebih cemerlang dan pastinya kurang perhatian yang kurang perhatian.

Atau ini bermakna bahawa soalan ujian mempunyai tahap kesukaran yang sangat berbeza.

Lengkung B adalah mesokurik, menunjukkan bahawa keputusan ujian mengikuti taburan normal. Ini biasanya merupakan kes yang paling kerap.

Diselesaikan contoh curtosis

Cari pekali penunjuk Fisher untuk gred berikut, yang diperolehi dalam peperiksaan fizik kepada sekumpulan pelajar, dengan skala dari 1 hingga 10:

5, 5, 4, 7, 7.7, 9, 8, 9, 4, 3

Penyelesaian

Ekspresi berikut akan digunakan untuk data yang tidak dikelilingi, yang diberikan dalam bahagian sebelumnya:

Dengan pekali titik Fisher yang diberikan oleh:

Boleh melayani anda: Identiti Pythagorean: Demonstrasi, Contoh, Latihan

K = g₂ - 3

Nilai ini membolehkan mengetahui jenis pengedaran.

Untuk mengira g₂ Adalah mudah untuk melakukannya dengan teratur, langkah demi langkah, kerana beberapa operasi aritmetik mesti diselesaikan.

Langkah 1

Pertama, purata kelayakan dikira. Terdapat n = 11 data.

X = (5+5+4+7+7+7+9+8+9+4+3)/11 = 6.182

Langkah 2

Penyimpangan piawai dijumpai, yang mana persamaan ini digunakan:

 Dengan menggunakan kalkulator dengan fungsi statistik, hasilnya segera:

σ = 1.992

Atau anda juga boleh membina meja, yang juga diperlukan untuk langkah seterusnya dan di mana setiap istilah ringkasan yang diperlukan ditulis, bermula dengan (x_Yo - X), kemudian (x_Yo - X)² Dan kemudian (x_Yo - X)⁴ :

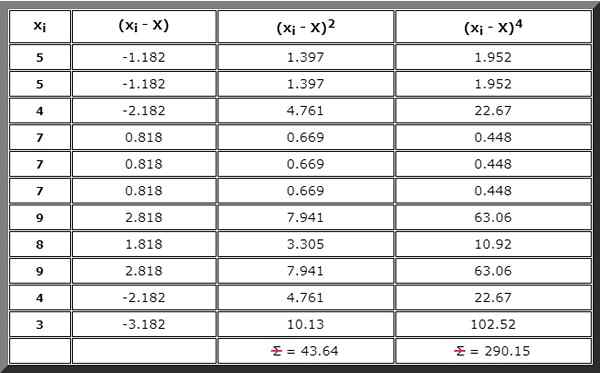
Langkah 3

Menjalankan jumlah yang ditunjukkan dalam pengangka formula untuk g₂. Untuk ini, hasil lajur kanan jadual sebelumnya digunakan:

Σ (x_Yo - X)⁴= 290.lima belas

Oleh itu:

g₂ = (1/11) x 290.15/1.992⁴ = 1.675

Koefisien papan tanda Fisher adalah:

K = g₂ - 3 = 1.675 - 3 = -1.325

Apa kepentingan adalah tanda hasilnya, yang, apabila negatif, sepadan dengan platitud tahap kesukaran yang berlainan.

Penggunaan spreadsheet seperti Excel, sangat memudahkan resolusi jenis masalah ini dan juga menawarkan pilihan untuk graf pengedaran.

Rujukan

1. Levin, r. 1988. Statistik untuk pentadbir. 2. Edisi. Prentice Hall.
2. Marco, f. Curtosis. Pulih dari: Economipedia.com.
3. Oliva, j. Asimetri dan curtosis. Diperolehi daripada: statistikAUCV.Fail.WordPress.com.
4. Spurr, w. 1982. Membuat keputusan dalam pentadbiran. Limusa.
5. Wikipedia. Kurtosis. Diperoleh dari: dalam.Wikipedia.org.