Jenis Aksioms Kebarangkalian, Penjelasan, Contoh, Latihan

The aksioma kebarangkalian Mereka adalah cadangan matematik mengenai teori kebarangkalian, yang tidak merit demonstrasi. The Axioms ditubuhkan pada tahun 1933 oleh ahli matematik Rusia Andrei Kolmogorov (1903-1987) dalam karyanya Asas teori kebarangkalian dan meletakkan asas kajian kebarangkalian matematik.

Apabila menjalankan eksperimen rawak tertentu ξ, ruang sampel adalah bersama dengan semua hasil eksperimen yang mungkin, juga dipanggil peristiwa. Sebarang peristiwa dilambangkan sebagai a dan p (a) adalah kebarangkalian berlaku. Kemudian Kolmogorov menegaskan bahawa:

Rajah 1. Aksioma kebarangkalian membenarkan untuk mengira kebarangkalian memukul perjudian seperti rolet. Sumber: Pixabay.

-Axioma 1 (tiada negatif): Kebarangkalian bahawa sebarang peristiwa berlaku sentiasa positif atau sifar, P (a) ≥0. Apabila kebarangkalian peristiwa adalah 0, ia dipanggil Peristiwa yang mustahil.

-Axioma 2 (kepastian): dengan syarat bahawa beberapa peristiwa yang dimiliki oleh E, kebarangkalian kejadiannya adalah 1, yang dapat kita nyatakan P (e) = 1. Adalah apa yang dikenali sebagai Acara selamat, Oleh kerana semasa melakukan eksperimen, terdapat hasil dengan kepastian.

-Axioma 3 (tambahan): Dalam kes dua atau lebih peristiwa tidak serasi dua hingga dua, dipanggil ke₁, Ke₂, Ke₃..., kebarangkalian acara itu₁ lebih banyak a₂ lebih banyak a₃ Dan sebagainya, ia adalah jumlah kebarangkalian bahawa masing -masing berlaku secara berasingan.

Ini dinyatakan sebagai: P (a₁ U a₂ U a₃ U ...) = p (a₁) + P (a₂) + P (a₃) +..

Rajah 2. Ahli matematik Rusia yang luar biasa Andrei Kolmogorov (1903-1987), yang meletakkan asas untuk kebarangkalian aksiomatik. Sumber: Wikimedia Commons.

[TOC]

Contoh

Kebarangkalian aksioma digunakan secara meluas dalam banyak aplikasi. Sebagai contoh:

Cakar atau Tachuela dibuang ke udara, dan apabila lantai jatuh, ada pilihan untuk jatuh dengan hujung (u) atau dengan hujung (d) (kita tidak akan menganggap kemungkinan lain). Ruang sampel eksperimen ini terdiri daripada peristiwa -peristiwa ini, maka E = u, d.

Boleh melayani anda: pepejal revolusi: kelantangan, jenis, latihan yang diselesaikanRajah 3. Dalam percubaan melancarkan Tachuela terdapat dua peristiwa kebarangkalian yang berbeza: jatuh dengan hujung atau ke lantai. Sumber: Pixabay.

Dengan menggunakan aksioma yang kita ada:

P (e) = 1 (Axioma 2)

Tetapi P (e) = p (u) + p (d) (Axioma 3), kerana peristiwa -peristiwa ini tidak serasi, atau disjoint. Pepijat tidak jatuh dengan hujung atas atau ke bawah pada masa yang sama, ia adalah satu atau yang lain, tetapi tidak kedua -duanya, kerana kemungkinan lain sedang dipertimbangkan. Jadi:

P (u) + p (d) = 1

P (u) = 1 - p (d)

Sekiranya ia sama -sama mungkin jatuh dengan tip ke atas atau ke bawah, P (u) = p (d) = ½ (Axioma 1). Walau bagaimanapun, mungkin disebabkan oleh pembinaan dan reka bentuk pepijat. Contohnya, mungkin itu P (u) = ¾ manakala P (d) = ¼ (Axioma 1).

Perhatikan bahawa dalam kedua -dua kes, jumlah kebarangkalian memberikan 1. Walau bagaimanapun, aksioma tidak menunjukkan bagaimana untuk memperuntukkan kebarangkalian, sekurang -kurangnya tidak sepenuhnya. Tetapi mereka mengesahkan bahawa mereka adalah nombor antara 0 dan 1 dan itu, seperti yang berlaku dalam kes ini, jumlah semua adalah 1.

Cara untuk memberikan kebarangkalian

Kebarangkalian aksioma tidak membentuk kaedah untuk memberikan nilai kebarangkalian. Untuk ini terdapat tiga pilihan yang serasi dengan aksioma:

Peraturan Laplace

Setiap peristiwa diberikan kebarangkalian yang sama berlaku, maka kebarangkalian kejadian ditakrifkan sebagai:

P (a) = bilangan kes yang menggalakkan pada peristiwa a/ bilangan kes yang mungkin

Sebagai contoh, apakah kebarangkalian mengekstrak ace dari dek kad Perancis? Dek mempunyai 52 kad, 13 dari setiap tongkat dan terdapat 4 tongkat. Setiap tongkat mempunyai 1, jadi secara keseluruhan terdapat 4 aces:

P (AS) = 4/52 = 1/13

Peraturan Laplace terhad kepada ruang sampel terhingga, di mana setiap peristiwa mungkin sama.

Boleh melayani anda: Matematik diskret

Frekuensi relatif

Di sini eksperimen harus diulang, kerana kaedah ini berdasarkan kepada sebilangan besar pengulangan.

Mari kita membuat pengulangan eksperimen ξ, yang mana kita dapati bahawa n adalah bilangan kali yang berlaku peristiwa tertentu a, maka kebarangkalian bahawa peristiwa ini akan berlaku adalah:

P (a) = lim_{I → ∞} (Tidak)

Di mana n/i adalah kekerapan relatif peristiwa.

Tentukan P (a) dengan cara ini memenuhi aksioma Kolmogorov, tetapi ia mempunyai kesulitan yang banyak ujian mesti dilakukan supaya kebarangkalian sesuai.

Kaedah subjektif

Seseorang atau sekumpulan orang boleh bersetuju untuk memberikan kebarangkalian kepada peristiwa, melalui penghakiman mereka sendiri. Kaedah ini mempunyai kelemahan bahawa orang yang berbeza dapat memberikan kebarangkalian yang berbeza ke acara yang sama.

Latihan diselesaikan

Dalam eksperimen secara serentak melancarkan 3 mata wang jujur, mendapatkan peluang peristiwa yang diterangkan:

a) 2 muka dan salib.

b) 1 muka dan dua salib

c) 3 salib.

d) sekurang -kurangnya 1 muka.

Penyelesaian kepada

Wajah dilambangkan dengan C dan salib dengan x. Tetapi ada beberapa cara untuk mendapatkan dua muka dan salib. Sebagai contoh, dua syiling pertama boleh jatuh dengan muka dan yang ketiga dengan Cruz. Atau yang pertama boleh jatuh muka, salib kedua dan wajah ketiga. Dan akhirnya yang pertama boleh menjadi salib dan baki wajah.

Untuk menjawab soalan -soalan yang diperlukan untuk mengetahui semua kemungkinan, yang diterangkan dalam alat yang dipanggil Rajah pokok Sama ada Kebarangkalian pokok:

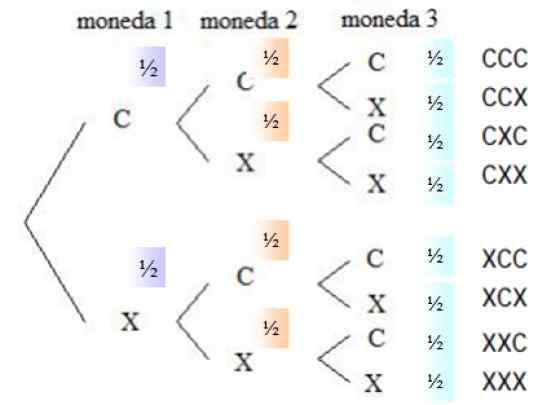Rajah 4. Diagram Pokok Untuk Pelancaran Serentak Tiga Syiling Jujur. Sumber: f. Zapata.

Kebarangkalian bahawa dalam mana -mana mata wang mahal adalah ½, perkara yang sama berlaku untuk salib, kerana mata wang itu jujur. Di lajur yang betul, semua kemungkinan pelancaran disenaraikan, iaitu ruang sampel.

Boleh melayani anda: Pembolehubah statistik

Gabungan yang bertindak balas terhadap acara yang diminta dipilih dari ruang sampel, kerana urutan di mana wajah kelihatan tidak penting. Terdapat tiga acara yang menggalakkan: CCX, CXC dan XCC. Kebarangkalian setiap peristiwa adalah:

P (ccx) = ½. ½ . ½ = 1/8

Perkara yang sama berlaku untuk peristiwa CXC dan XCC, masing -masing mempunyai kebarangkalian 1/8 berlaku. Oleh itu, kebarangkalian mendapatkan tepat 2 muka adalah jumlah kebarangkalian semua peristiwa yang baik:

P (2 muka) = 1/8 + 1/8 + 1/8 = 3/8 = 0.375

Penyelesaian b

Mencari kebarangkalian bahawa terdapat dua salib yang tepat adalah masalah yang sama dengan yang sebelumnya, terdapat juga tiga peristiwa yang baik yang diambil dari ruang sampel: CXX, XCX dan XXC. Oleh itu:

P (2 salib) = 3/8 = 0.375

Penyelesaian c

Secara intuitif tahu bahawa kebarangkalian mendapatkan 3 salib (atau 3 muka) lebih rendah. Dalam kes ini, acara yang dicari adalah xxx, pada akhir lajur kanan, yang kebarangkaliannya:

P (xxx) = ½. ½. ½ = 1/8 = 0.125.

Penyelesaian d

Diminta untuk mendapatkan sekurang -kurangnya 1 muka, ini bermakna 3 muka, 2 muka atau 1 muka boleh meninggalkan. Satu -satunya acara yang tidak serasi dengan ini adalah satu di mana 3 salib keluar, kebarangkaliannya adalah 0.125. Oleh itu kebarangkalian yang dicari adalah:

P (sekurang -kurangnya 1 muka) = 1 - 0.125 = 0.875.

Rujukan

1. Canavos, g. 1988. Kebarangkalian dan Statistik: Aplikasi dan Kaedah. McGraw Hill.
2. DEVORE, J. 2012. Kebarangkalian dan statistik untuk kejuruteraan dan sains. Ke -8. Edisi. Cengage.
3. Lipschutz, s. 1991. Siri Schaum: Kebarangkalian. McGraw Hill.
4. Obregón, i. 1989.Teori kebarangkalian. Editorial Limusa.
5. Walpole, r. 2007. Kebarangkalian dan statistik untuk kejuruteraan dan sains. Pearson.