Data tidak dikumpulkan contoh dan senaman diselesaikan

The Data yang tidak berkumpul Mereka adalah yang, yang diperoleh dari kajian, belum dianjurkan oleh kelas. Apabila ia adalah bilangan data yang boleh diurus, biasanya 20 atau kurang, dan terdapat beberapa data yang berbeza, mereka boleh dianggap sebagai tidak dikumpulkan dan mengeluarkan maklumat berharga dari mereka.

Data yang tidak berkumpul datang dari tinjauan atau kajian yang dijalankan untuk mendapatkannya dan oleh itu kekurangan pemprosesan. Mari lihat beberapa contoh:

Rajah 1. Data yang tidak digabungkan datang terus dari mana -mana kajian dan belum diklasifikasikan. Sumber: Pxhere.

-Keputusan peperiksaan CI pekali intelektual di 20 pelajar rawak dari universiti. Data yang diperoleh adalah seperti berikut:

119, 109, 124, 119, 106, 112, 112, 112, 112, 109, 112, 124, 109, 109, 109, 106, 124, 112, 112,106

-Umur 20 pekerja kafeteria yang sangat popular:

24, 20, 22, 19, 18, 27, 25, 19, 27, 18, 21, 22, 23, 19, 22, 27, 29, 23, 20

-Nota akhir purata 10 pelajar kelas matematik:

3.2; 3.1; 2,4; 4.0; 3.5; 3.0; 3.5; 3.8; 4.2; 4.9

[TOC]

Sifat data

Terdapat tiga sifat penting yang mencirikan satu set data statistik dikumpulkan atau tidak, iaitu:

-Kedudukan, yang merupakan kecenderungan data yang akan dikumpulkan sekitar nilai -nilai tertentu.

-Penyebaran, Menunjukkan bagaimana tersebar atau disebarkan adalah data di sekitar nilai tertentu.

-Bentuk, Ia merujuk kepada cara di mana data diedarkan, yang dapat dilihat apabila grafnya dibina. Terdapat lengkung yang sangat simetri dan juga berat sebelah, sama ada di sebelah kiri atau di sebelah kanan nilai pusat tertentu.

Bagi setiap sifat ini terdapat beberapa langkah yang menggambarkannya. Setelah diperoleh, mereka memberi kami panorama tingkah laku data:

-Langkah kedudukan yang paling banyak digunakan adalah aritmetik min atau hanya sederhana, median dan fesyen.

-Dalam penyebaran julat, varians dan sisihan piawai sering digunakan, tetapi mereka bukan satu -satunya langkah penyebaran.

Boleh melayani anda: homotecia

-Dan untuk menentukan borang, purata dan median dibandingkan dengan kecenderungan, seperti yang akan dilihat tidak lama lagi.

Pengiraan purata, median dan fesyen

-Maksud aritmetik, Juga dikenali sebagai purata dan dilambangkan sebagai x, ia dikira seperti berikut:

X = (x₁ + x₂ + x₃ +... x_n) / n

Di mana x₁, x₂,… . x_n, adakah data dan n adalah jumlahnya. Dalam penjumlahan Jumlah terdapat:

Di sini indeks saya mewakili data 1, data 2, data 3 dan sebagainya, sehingga mencapai satu -satunya, yang terakhir.

-Median Ia adalah nilai yang muncul di tengah -tengah penggantian data yang teratur, jadi untuk mendapatkannya, adalah perlu untuk memerintahkan data terlebih dahulu.

Sekiranya bilangan pemerhatian adalah ganjil, tidak ada masalah dalam mencari titik tengah set, tetapi jika kita mempunyai sepasang data, kedua -dua data pusat dicari dan purata.

-Fesyen Ia adalah nilai yang paling biasa diperhatikan dalam set data. Ia tidak selalu wujud, kerana mungkin tidak ada nilai yang diulangi lebih kerap daripada yang lain. Terdapat juga dua data dengan kekerapan yang sama, di mana terdapat perbincangan mengenai pengedaran bi-modal.

Tidak seperti dua langkah sebelumnya, fesyen boleh digunakan dengan data kualitatif.

Mari lihat bagaimana langkah -langkah kedudukan ini dikira dengan contoh:

Contoh yang diselesaikan

Katakan anda ingin menentukan purata aritmetik, median dan fesyen dalam contoh yang dicadangkan pada mulanya: umur 20 pekerja kafeteria:

24, 20, 22, 19, 18, 27, 25, 19, 27, 18, 21, 22, 23, 19, 22, 27, 29, 23, 20

The separuh Ia dikira hanya dengan menambahkan semua nilai dan membahagikan dengan n = 20, iaitu jumlah data. Cara ini:

Boleh melayani anda: Hubungan perkadaran: konsep, contoh dan latihan

X = (24 + 20 + 22 + 19 + 18 + 27+ 25 + 19 + 27 + 18 + 21 + 22 + 23 + 21+ 19 + 22 + 27+ 29 + 23+ 20) / 20 =

= 22.3 tahun.

Untuk mencari median Adalah perlu untuk memerintahkan set data terlebih dahulu:

18, 18, 19, 19, 19, 20, 20, 21, 21, 22, 22, 22, 23, 23, 24, 25, 27, 27, 27, 29

Seperti beberapa data, kedua -dua data pusat, yang diketengahkan dengan berani, diambil, dan purata. Kerana kedua -duanya adalah 22, median adalah 22 tahun.

Akhirnya, fesyen Hakikat yang paling banyak diulang atau kekerapannya yang lebih besar, iaitu 22 tahun ini.

Julat, varians, sisihan piawai dan kecenderungan

Julat ini hanyalah perbezaan antara utama dan paling sedikit data dan membolehkan kebolehubahan mereka dengan cepat menghargai. Tetapi terdapat langkah -langkah penyebaran lain yang menawarkan lebih banyak maklumat mengenai pengedaran data.

Varians dan sisihan piawai

Varians dilambangkan sebagai s dan dikira dengan ekspresi:

Ia sering bekerja dengan quasiriance dan bukannya varians, yang dikira dengan cara yang sama, hanya dibahagikan dengan N-1, bukannya melakukan antara N:

Oleh kerana varians adalah jumlah kuadrat, menghasilkan kuadrat unit sampel. Sebagai contoh, dalam kajian umur pekerja di kafeteria, varians akan datang bertahun -tahun².

Kemudian untuk mentafsirkan hasilnya dengan betul, sisihan piawai seperti akar kuadrat varians, atau juga pengurangan kuasi standard ditakrifkan, yang merupakan akar kuasi kuasi:

Bias

Ia adalah perbandingan antara purata x dan median med:

-Ya med = media x: data simetri.

-Ketika x> med: berat sebelah ke kanan.

-Dan jika x < Med: los datos sesgan hacia la izquierda.

Latihan diselesaikan

Cari purata, median, fesyen, pangkat, varians, sisihan piawai dan kecenderungan untuk hasil peperiksaan pekali intelektual sebanyak 20 pelajar dari universiti:

Boleh melayani anda: fungsi matematik

119, 109, 124, 119, 106, 112, 112, 112, 112, 109, 112, 124, 109, 109, 109, 106, 124, 112, 112, 106

Penyelesaian

Kami akan memesan data, kerana perlu mencari median.

106, 106, 106, 109, 109, 109, 109, 109, 112, 112, 112, 112, 112, 112, 119, 119, 124, 124, 124

Dan kami akan memasukkannya ke dalam meja seperti berikut, untuk memudahkan pengiraan. Lajur kedua bertajuk "terkumpul" adalah jumlah data yang sepadan ditambah sebelumnya.

Lajur ini dengan mudah akan menemui purata, membahagikan yang terakhir terkumpul antara jumlah data, seperti yang dilihat pada akhir lajur "terkumpul":

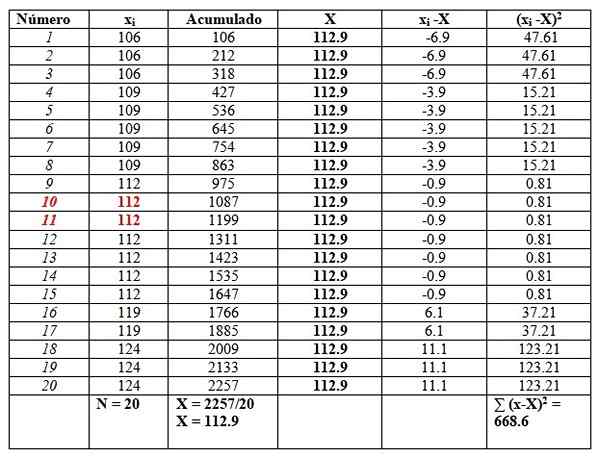
X = 112.9

Median adalah purata data pusat yang diserlahkan dengan warna merah: Nombor 10 dan nombor 11. Seperti yang sama, median adalah 112.

Akhirnya, fesyen adalah nilai yang paling berulang dan 112, dengan 7 pengulangan.

Bagi langkah penyebaran, julatnya ialah:

124-106 = 18.

Varians diperolehi dengan membahagikan hasil akhir lajur kanan antara n:

S = 668.6/20 = 33.42

Dalam kes ini, sisihan piawai adalah akar kuadrat varians: √33.42 = 5.8.

Sebaliknya, nilai -nilai quasivarian dan sisihan piawai kuasi adalah:

s_c= 668.6/19 = 35.2

Penyataan kuasi standard = √35.2 = 5.9

Akhirnya, bias sedikit ke kanan, kerana purata 112.9 lebih besar daripada median 112.

Rujukan

1. Berenson, m. 1985. Statistik untuk Pentadbiran dan Ekonomi. Inter -American s.Ke.
2. Canavos, g. 1988. Kebarangkalian dan Statistik: Aplikasi dan Kaedah. McGraw Hill.
3. DEVORE, J. 2012. Kebarangkalian dan statistik untuk kejuruteraan dan sains. Ke -8. Edisi. Cengage.
4. Levin, r. 1988. Statistik untuk pentadbir. 2. Edisi. Prentice Hall.
5. Walpole, r. 2007. Kebarangkalian dan statistik untuk kejuruteraan dan sains. Pearson.