Darjah kebebasan bagaimana mengira mereka, jenis, contoh

The darjah kebebasan Dalam statistik adalah bilangan komponen bebas vektor rawak. Sekiranya vektor mempunyai n komponen dan ada p persamaan linear yang mengaitkan komponennya, maka darjah kebebasan Ia adalah n-p.

Konsep darjah kebebasan Ia juga muncul dalam mekanik teoritis, di mana dalam mod kasar mereka bersamaan dengan dimensi ruang di mana zarah bergerak, kecuali bilangan ligatur.

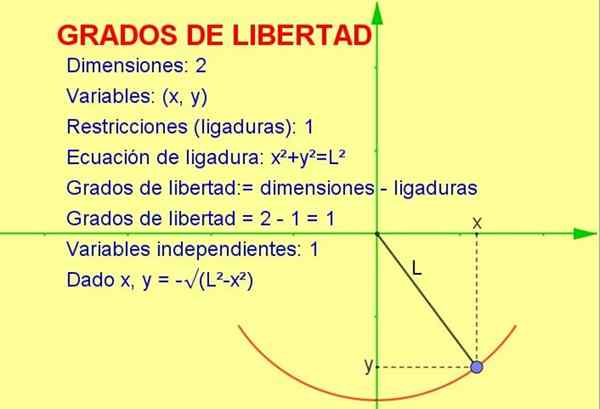
Rajah 1. Pendulum bergerak dalam dua dimensi, tetapi hanya mempunyai tahap kebebasan kerana ia diwajibkan untuk bergerak dalam arka radius l l l. Sumber: f. Zapata.

Artikel ini akan membincangkan konsep darjah kebebasan yang digunakan untuk statistik, tetapi contoh mekanikal lebih mudah untuk digambarkan dengan cara geometri.

[TOC]

Jenis darjah kebebasan

Menurut konteks di mana ia digunakan, cara mengira bilangan darjah kebebasan boleh berbeza -beza, tetapi idea yang mendasari selalu sama: jumlah dimensi kurang bilangan sekatan.

Dalam kes mekanikal

Pertimbangkan zarah yang berayun terikat dengan tali (pendulum) yang bergerak dalam satah menegak x-y (2 dimensi). Walau bagaimanapun, zarah diwajibkan untuk bergerak ke lilitan radius sama dengan panjang tali.

Oleh kerana zarah hanya dapat bergerak pada lengkung itu, bilangan darjah kebebasan Ia adalah 1. Ini dapat digambarkan dalam Rajah 1.

Cara untuk mengira bilangan darjah kebebasan adalah untuk membuat perbezaan bilangan dimensi kecuali bilangan sekatan:

Darjah kebebasan: = 2 (dimensi) - 1 (ligation) = 1

Penjelasan lain yang membolehkan kita mencapai hasilnya adalah seperti berikut:

-Kami tahu bahawa kedudukan dua dimensi diwakili oleh titik koordinat (x, y).

-Tetapi sebagai titik mesti memenuhi persamaan lilitan (x² + dan² = L²) Untuk nilai pembolehubah x yang diberikan, pembolehubah dan ditentukan oleh persamaan atau sekatan tersebut.

Dengan cara ini, hanya satu daripada pembolehubah yang bebas dan sistemnya Satu (1) tahap kebebasan.

Boleh melayani anda: kebarangkalian klasik: pengiraan, contoh, latihan yang diselesaikan

Dalam satu set nilai rawak

Untuk menggambarkan apa maksud konsepnya mengandaikan vektor

x = (x₁, x₂,..., x_n)

Mewakili sampel n Nilai rawak biasanya diedarkan. Dalam kes ini vektor rawak x mempunyai n komponen bebas dan oleh itu dikatakan bahawa x mempunyai n darjah kebebasan.

Mari buat vektor sekarang r sisa

r = (x₁ - , x₂ - ,… ., x_n - )

Di mana ia mewakili purata sampel, yang dikira seperti berikut:

= (x₁ + x₂ +… .+ x_n) / n

Kemudian jumlahnya

(x₁ - )+(x₂ - )+.. .+(x_n - ) = (x₁ + x₂ +… .+ x_n) - n = 0

Ia adalah persamaan yang mewakili sekatan (atau ligation) dalam elemen vektor r sisa, kerana jika n-1 diketahui, komponen vektor r, Persamaan sekatan menentukan komponen yang tidak diketahui.

Oleh itu vektor r dimensi n dengan sekatan:

Σ (x_Yo - ) = 0

Mempunyai (N - 1) darjah kebebasan.

Sekali lagi ia digunakan bahawa pengiraan bilangan darjah kebebasan adalah:

darjah kebebasan: = n (dimensi) - 1 (sekatan) = n -1

Contoh

Varians dan darjah kebebasan

Varians s² Ia ditakrifkan sebagai purata kuadrat penyimpangan (atau sisa) sampel data:

s² = (r•r) / (N-1)

di mana r adalah vektor sisa r = (x1 -, x2 -, .. ., Xn -) dan titik tebal (•) adalah pengendali produk skalar. Sebagai alternatif, formula varians boleh ditulis seperti berikut:

s² = Σ (x_Yo - )² / (N-1)

Walau apa pun, perlu diperhatikan bahawa apabila mengira purata kuadrat sisa, ia dibahagikan dengan (n-1) dan bukan antara n, kerana seperti yang dibincangkan di bahagian sebelumnya, bilangan darjah kebebasan vektor r adalah (n-1).

Jika untuk pengiraan varians ia dibahagikan antara n Bukannya (n-1), hasilnya akan mempunyai kecenderungan yang sangat penting untuk nilai n kurang daripada 50.

Ia dapat melayani anda: geometri analisis

Dalam kesusasteraan juga muncul formula varians dengan pembahagi n bukan (n-1), ketika datang ke varians penduduk.

Tetapi set pemboleh ubah rawak sisa, yang diwakili oleh vektor r, Walaupun ia mempunyai dimensi n, ia hanya mempunyai (n-1) darjah kebebasan. Walau bagaimanapun, jika nombor data cukup besar (n> 500), kedua -dua formula berkumpul dengan hasil yang sama.

Kalkulator dan spreadsheet menawarkan dua versi varians dan sisihan piawai (yang merupakan akar kuadrat varians).

Cadangan kami, memandangkan analisis yang dibentangkan di sini, adalah untuk sentiasa memilih versi dengan (n-1) setiap kali perlu untuk mengira varians atau sisihan piawai, untuk mengelakkan hasil dengan bias.

Dalam taburan Chi Square

Beberapa pengagihan kebarangkalian dalam pemboleh ubah rawak berterusan bergantung pada parameter yang dipanggil darjah kebebasan, Ini adalah kes pengedaran persegi chi (χ²).

Nama parameter tersebut datang hanya dari tahap kebebasan vektor rawak yang mendasari pengedaran ini.

Anggapkan bahawa terdapat populasi g, yang mana sampel s saiz diambil:

X₁ = (x1₁, x1₂,... x1_n)

X2 = (x2₁, x2₂,... x2_n)

… .

X_J = (xj₁, xj₂,... xj_n)

… .

Xg = (xg₁, Xg₂,... xg_n)

Penduduk J yang mempunyai sisihan purata dan piawai SJ, Ikuti pengedaran normal n (, SJ ).

ZJ pembolehubah yang dinamakan atau dinormalisasi_Yo ditakrifkan sebagai:

ZJ_Yo = (xj_Yo - ) / SJ.

Dan vektor ZJ Ia ditakrifkan seperti ini:

ZJ = (ZJ₁, ZJ₂,..., ZJ_Yo,..., ZJ_n) Dan ikuti pengedaran normal n (0.1).

Kemudian pemboleh ubah:

Q = ((Z1₁ ^2 + z2₁^2+.. . + Zg₁^2), .. ., (Z1_n^2 + z2_n^2+.. . + Zg_n^2))

Ikuti pengedaran χ²(g) dipanggil Pengedaran chi persegi dengan tahap kebebasan g.

Dalam kontras hipotesis (dengan contoh yang diselesaikan)

Apabila anda ingin membuat kontras hipotesis berdasarkan set data rawak tertentu, perlu mengetahui Bilangan darjah kebebasan g Untuk dapat menggunakan ujian Square Chi.

Boleh melayani anda: Pengagihan seragam yang berterusan: Ciri, contoh, aplikasi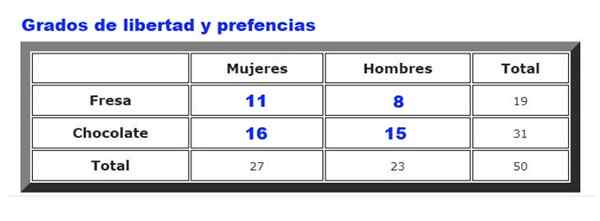 Rajah 2. Adakah hubungan antara rasa ais krim dan jantina pelanggan? Sumber: f. Zapata.

Sebagai contoh, data yang dikumpulkan pada pilihan ais krim coklat atau strawberi antara lelaki dan wanita di beberapa kedai ais krim akan dianalisis. Kekerapan yang lelaki dan wanita memilih strawberi atau coklat, diringkaskan dalam Rajah 2.

Pertama, jadual kekerapan yang diharapkan dikira, yang dibuat dengan mengalikan Jumlah baris untuk dia Jumlah lajur, dibahagikan dengan Jumlah data. Hasilnya ditunjukkan dalam angka berikut:

Rajah 3. Pengiraan frekuensi yang dijangkakan berdasarkan frekuensi yang diperhatikan (nilai biru dalam Rajah 2). Sumber: f. Zapata.

Kemudian kami meneruskan untuk mengira persegi chi (dari data) dengan formula berikut:

χ² = Σ (f_{Sama ada} - F_dan)² / F_dan

Di mana f_{Sama ada} adalah frekuensi yang diperhatikan (Rajah 2) dan f_dan adalah frekuensi yang diharapkan (Rajah 3). Jumlahnya adalah lebih dari semua pangkat dan lajur, yang dalam contoh kami memberi empat syarat.

Setelah melakukan operasi yang anda dapat:

χ² = 0.2043.

Kini perlu dibandingkan dengan dataran teoritis, yang bergantung pada Bilangan darjah kebebasan g.

Dalam kes kami nombor ini ditentukan seperti berikut:

G = (#filas - 1) (#columnas - 1) = (2 - 1) (2 - 1) = 1 * 1 = 1.

Ternyata bilangan darjah kebebasan g contoh ini ialah 1.

Jika anda ingin mengesahkan atau menolak hipotesis nol (H0: tidak ada korelasi antara rasa dan jantina) dengan tahap kepentingan 1%, persegi chi teoritis dikira dengan tahap kebebasan g = 1.

Nilai yang menjadikan kekerapan terkumpul dicari (1 - 0.01) = 0.99, iaitu 99%. Nilai ini (yang boleh diperoleh dari jadual) adalah 6.636.

Oleh kerana chi teoretikal melampaui yang dikira, maka hipotesis nol disahkan.

Iaitu, dengan data yang dikumpulkan, tidak ada hubungan antara rasa pembolehubah dan jantina.

Rujukan

1. Minitab. Berapakah darjah kebebasan? Diperolehi dari: Sokongan.Minitab.com.
2. Moore, David. (2009) Statistik Gunaan Asas. Editor Antoni Bosch.
3. Leigh, Jennifer. Cara mengira darjah kebebasan dalam model statistik. Pulih dari: geniolandia.com
4. Wikipedia. Ijazah Kebebasan (Statistik). Pulih dari: Adakah.Wikipedia.com
5. Wikipedia. Tahap kebebasan (fizikal). Pulih dari: Adakah.Wikipedia.com