Sifat derivatif separa, pengiraan, latihan

The derivatif separa fungsi dengan beberapa pembolehubah bebas adalah yang dicapai dengan mengambil derivatif biasa dalam salah satu pembolehubah, sementara yang lain dikekalkan atau diambil sebagai pemalar.

Derivatif separa dalam salah satu pembolehubah, menentukan bagaimana fungsi berbeza pada setiap titik, per unit perubahan pembolehubah yang dipersoalkan. 

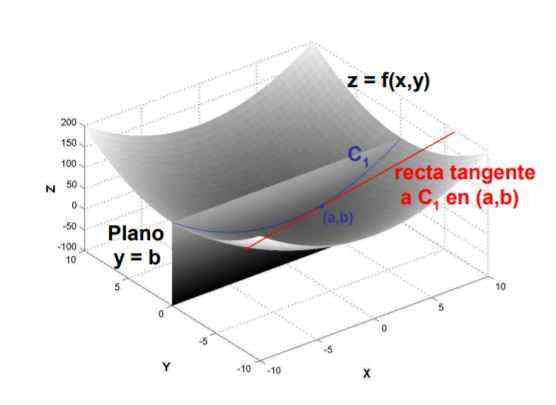Rajah 1. Cerun garis tangen ke lengkung yang dibentuk oleh persimpangan satah y = b dengan permukaan f (x, y) pada titik (a, b) adalah derivatif separa f berkenaan dengan x, dinilai pada ketika itu. Sumber: UPM.adalah

Oleh kerana takrifannya, derivatif separa dikira dengan mengambil had matematik dari kota antara variasi fungsi dan variasi pemboleh ubah berkenaan dengan apa yang diperolehi, apabila perubahan yang terakhir cenderung kepada sifar.

Katakan kes fungsi F Ia bergantung pada pembolehubah x dan dan, iaitu untuk setiap pasangan (X, y) A ditugaskan z: 

f: (x, y) → z .

Terbitan separa fungsi z = f (x, y), berkenaan dengan x ditakrifkan sebagai:

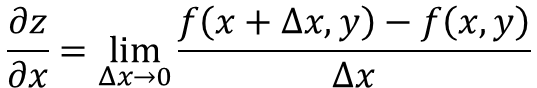
Sekarang, terdapat beberapa cara untuk menunjukkan derivatif separa fungsi, sebagai contoh:

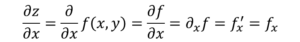
Perbezaan dengan derivatif biasa, dari segi notasi, adalah bahawa d terbitan ditukar kepada simbol ∂, Dikenali sebagai "Jacobi D".

[TOC]

Sifat derivatif separa

Derivatif separa fungsi beberapa pembolehubah, berkenaan dengan salah satu daripada mereka, adalah derivatif biasa dalam pemboleh ubah tersebut dan mempertimbangkan yang lain sebagai tetap atau tetap. Untuk mencari derivatif separa, peraturan terbitan derivatif biasa boleh digunakan.

Di bawah sifat utama:

Boleh melayani anda: Faktor umum untuk istilah pengelompokan: Contoh, Latihan

Kesinambungan

Jika fungsi f (x, y) mempunyai derivatif separa di x dan dan pada titik (Xo, saya) maka dapat dikatakan bahawa fungsi itu berterusan pada ketika itu.

Peraturan rantai

Fungsi f (x, y) Dengan derivatif separa berterusan di x dan dan, yang seterusnya bergantung pada parameter t melalui x = x (t) dan y = y (t), Ia mempunyai derivatif biasa berkenaan dengan pemboleh ubah t, yang dikira oleh peraturan rantai:

d_t Z = ∂_xz d_tx + ∂_danz d_tdan

Menutup atau mengunci harta tanah

Terbitan separa berkenaan dengan salah satu pemboleh ubah fungsi F dua atau lebih pembolehubah (X, y, ...), Ia adalah fungsi lain g Dalam pembolehubah yang sama, sebagai contoh: 

G (x, y, ...) = ∂_dan f (x, y, ...)

Iaitu, terbitan separa adalah operasi yang berlaku dari rⁿ a rⁿ. Dalam erti kata itu dikatakan bahawa ia adalah Operasi tertutup.

Derivatif separa berturut -turut

Derivatif separa berturut -turut fungsi beberapa pembolehubah dapat ditakrifkan, menimbulkan fungsi baru dalam pembolehubah bebas yang sama.

Menjadi fungsi f (x, y). Derivatif berturut -turut berikut boleh ditakrifkan:

F_Xx = ∂_xF ;  F_Yy = ∂_YyF ; F_Xy = ∂_XyF dan F_Yx = ∂_YxF

Dua yang terakhir dikenali sebagai Derivatif bercampur kerana mereka melibatkan dua pembolehubah bebas yang berbeza.

Teorem Schwarz

Menjadi fungsi f (x, y), ditakrifkan sedemikian rupa sehingga derivatif separa adalah fungsi berterusan dalam subset terbuka R².

Jadi, untuk setiap pasangan (X, y) Bahawa mereka tergolong dalam subset tersebut, derivatif campuran adalah sama:

∂_XyF = ∂_YxF

Pernyataan sebelumnya dikenali sebagai Teorem Schwarz.

Bagaimana derivatif separa dikira?

Derivatif separa dikira serupa dengan derivatif fungsi biasa dalam pemboleh ubah bebas tunggal. Apabila terbitan separa fungsi beberapa pembolehubah diambil berkenaan dengan salah satu daripada mereka, pembolehubah lain diambil sebagai pemalar.

Boleh melayani anda: separuh daripada 15

Berikut adalah beberapa contoh:

Contoh 1

Menjadi fungsi:

f (x, y) = -3x² + 2 (dan - 3)²

Diminta untuk mengira derivatif separa pertama berkenaan dengan x dan derivatif separa pertama berkenaan dengan dan.

Prosedur

Untuk mengira separa F berkenaan dengan x, Diambil dan sebagai tetap:

∂_xF = ∂_x(-3x² + 2 (dan - 3)² ) = ∂_x(-3x² )+ ∂_x(2 (dan - 3)² ) = -3 ∂_x(x²) + 0 = -6x.

Dan seterusnya, untuk mengira derivatif berkenaan dengan dan Diambil x sebagai tetap:

∂_danF = ∂_dan(-3x² + 2 (dan - 3)² ) = ∂_dan(-3x² )+ ∂_dan(2 (dan - 3)² ) = 0 + 2 · 2 (y - 3) = 4y - 12.

Contoh 2

Tentukan derivatif separa pesanan kedua:  ∂_Xxf, ∂_Yyf, ∂_YxF dan ∂_XyF Untuk fungsi yang sama F Contoh 1.

Prosedur

Dalam kes ini, kerana derivatif separa pertama telah dikira dalam x dan dan (Lihat Contoh 1):

∂_XxF = ∂_x(∂_xf) = ∂_x(-6x) = -6

∂_YyF = ∂_dan(∂_danf) = ∂_dan(4y - 12) = 4

∂_YxF = ∂_dan(∂_xf) = ∂_dan(-6x) = 0

∂_XyF = ∂_x(∂_danf) = ∂_x(4y - 12) = 0

Diperhatikan bahawa ∂_YxF = ∂_XyF, dengan itu memenuhi teorem Schwarz, kerana fungsi itu F dan derivatif separa pertama yang pertama adalah fungsi berterusan dalam R².

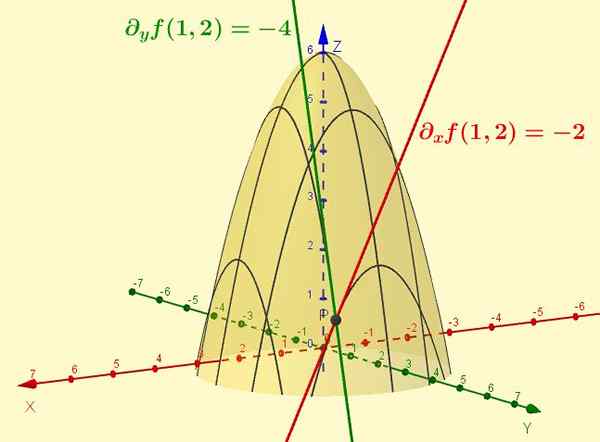
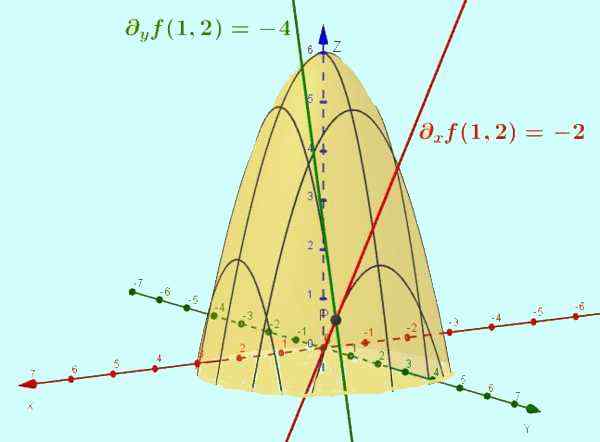Rajah 2. Fungsi z = f (x, y) = -x2 - y2 + 6 adalah permukaan yang ditunjukkan dalam angka. Derivatif separa berkenaan dengan x adalah cerun garis tangen lengkung yang hasil dari persimpangan permukaan tersebut dengan satah y = ctte (kes tertentu ditunjukkan y = 2). Begitu juga bahagian F berkenaan dengan dan adalah cerun tangen ke persimpangan dengan x = 1, pada titik (1, 2, 1).

Latihan yang diselesaikan

Latihan 1

Menjadi fungsi:

Boleh melayani anda: Kejayaan Kuadratik: Contoh, Peraturan dan Latihan Diselesaikan

f (x, y) = -x² - dan² + 6

Cari fungsi G (x, y) = ∂_xF  dan H (x, y) = ∂_danF.

Penyelesaian

Terbitan separa dari F berkenaan dengan x, yang mana pembolehubah dan Ia menjadi malar:

G (x, y) = - 2x

Begitu juga, terbitan separa g berkenaan dengan dan, melakukan x tetap, mengakibatkan fungsi h:

H (x, y) = -2y

Latihan 2 

Menilai untuk titik (1, 2) fungsi f (x, y) dan G (x, y) Latihan 1. Mentafsirkan hasilnya.

Penyelesaian

Nilai diganti x = 1 dan y = 2 memperoleh:

F (1,2) = -(1)² -(2)² + 6 = -5 + 6 = 1

Ini adalah nilai yang mengambil fungsi f apabila dinilai pada ketika itu.

Fungsinya f (x, y) Ia adalah permukaan dua dimensi dan koordinat z = f (x, y) Ia adalah ketinggian fungsi untuk setiap pasangan (X, y). Apabila pasangan itu diambil (1.2), Ketinggian permukaan f (x, y) adalah Z = 1.

Fungsinya G (x, y) = - 2x mewakili satah di ruang tiga dimensi yang persamaannya Z = -2x Wahai -2x + 0 dan -z = 0.

Kata kapal terbang berserenjang dengan kapal terbang Xz Dan pergi melalui titik (0, 0, 0). Apabila dinilai di x = 1 dan y = 2 Jadi Z = -2. Perhatikan bahawa nilai z = g (x, y) Ia bebas daripada nilai yang diberikan kepada pembolehubah dan.

Sebaliknya, jika permukaan bersilang f (x, y) Dengan pesawat y = c, dengan c tetap, anda mempunyai lengkung dalam pesawat Zx: z = -x² - c² + 6.

Dalam hal ini terbitan z berkenaan dengan x bertepatan dengan terbitan separa f (x, y) berkenaan dengan x: d_x Z = ∂_xF .

Semasa menilai pasangan (x = 1, y = 2) Terbitan separa pada ketika itu ∂_xF (1.2) Ia ditafsirkan sebagai cerun garis tangen ke lengkung z = -x² + 2 pada titik (x = 1, y = 2) Dan nilai cerun ini adalah -2.

Rujukan

1. Ayres, f. 2000. Pengiraan. 5ed. MC Graw Hill.
2. Derivatif separa fungsi dalam beberapa pembolehubah. Pulih dari: bangunan.UPM.adalah.
3. Leithold, l. 1992. Pengiraan dengan geometri analisis. Harla, s.Ke.
4. Purcell, e. J., Varberg, d., & Rigdon, s. Dan. (2007). Pengiraan. Mexico: Pendidikan Pearson.
5. Gorostizaga J. C. Derivatif separa. Pulih dari: ehu.Eus
6. Wikipedia. Derivatif separa. Pulih dari: Adakah.Wikipedia.com.