Perbezaan formula, persamaan, contoh, latihan

The Perbezaan kiub Ia adalah ungkapan algebra binomial bentuk ke³ - b³, di mana istilah a dan b boleh menjadi nombor sebenar atau ungkapan algebra dari pelbagai jenis. Contoh perbezaan kiub ialah: 8 - x³, Sejak 8 boleh ditulis sebagai 2³.

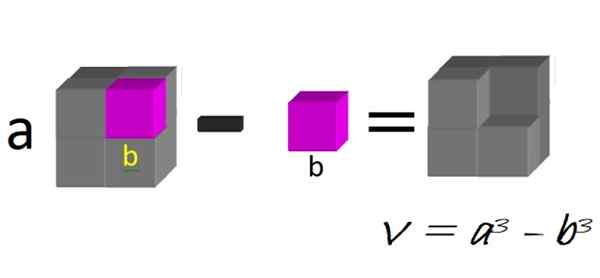
Secara geometri kita dapat memikirkan kiub besar, dari sisi A, yang mana bube kecil sisi b ditolak, seperti yang digambarkan dalam Rajah 1:

Rajah 1. Perbezaan kiub. Sumber: f. Zapata.

Jumlah angka yang dihasilkan adalah perbezaan dalam kiub:

V = a³ - b³

Untuk mencari ungkapan alternatif, diperhatikan bahawa angka ini dapat dipecahkan kepada tiga prisma, seperti yang ditunjukkan di bawah:

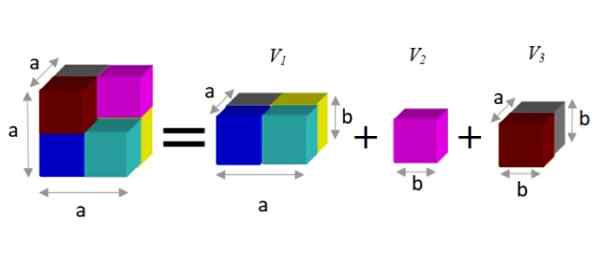Rajah 2. Perbezaan kiub (kiri kesamaan) adalah sama dengan jumlah jumlah separa (kanan). Sumber: f. Zapata.

Prisma mempunyai jumlah yang diberikan oleh produk tiga dimensi: Lebar x kedalaman x tinggi. Dengan cara ini, jumlah yang terhasil ialah:

V = a³ - b³ = a².b + b³ + ke.b²

Faktornya b Ia biasa di sebelah kanan. Di samping itu, dalam angka yang ditunjukkan di atas ia dipenuhi khususnya:

B = (A/2) ⇒ A = B + B

Oleh itu boleh dikatakan bahawa: b = a - b. Oleh itu:

ke³ - b³ = B (a² + b² +ke.b) = (a-b) (a² + ke.b + b²)

Cara ini menyatakan perbezaan kiub akan terbukti sangat berguna dalam banyak aplikasi dan akan diperoleh dengan cara yang sama, walaupun bahagian kiub yang hilang di sudut adalah berbeza dari b = a/2.

Perhatikan bahawa kurungan keduaIa kelihatan banyak kepada produk yang luar biasa dari segi empat, tetapi istilah silang tidak didarabkan dengan 2. Pembaca dapat mengembangkan sebelah kanan untuk mengesahkan bahawa ia diperoleh dengan berkesan ke³ - b³.

[TOC]

Boleh melayani anda: Binomial persegi

Contoh

Terdapat beberapa perbezaan kiub:

1 - m⁶

ke⁶b³ - 8Z¹²dan⁶

(1/125).x⁶ - 27.dan⁹

Mari kita analisa setiap satu daripada mereka. Dalam contoh pertama, 1 boleh ditulis sebagai 1 = 1³ dan istilah m⁶ Ia tetap: (m²)³. Kedua -dua istilah adalah kiub yang sempurna, oleh itu perbezaannya ialah:

1 -m⁶ = 1³ - (m²)³

Dalam contoh kedua, istilah ditulis semula:

ke⁶b³ = (a²b)³

8Z¹²dan⁶ = 2³ (z⁴)³ (dan²)³ = (2z⁴dan²)³

Perbezaan kiub ini adalah: (a²b)³ - (2Z⁴dan²)³.

Akhirnya, pecahan (1/125) adalah (1/5³), x⁶ = (x²)³, 27 = 3³ dan dan⁹ = (dan³)³. Menggantikan semua ini dalam ungkapan asal, ia diperolehi:

(1/125).x⁶  - 27y⁹ = [(1/5) (x²)]³ - (3y³)³

Pemfaktoran perbezaan kiub

Fakta Perbezaan kiub memudahkan banyak operasi algebra. Untuk melakukan ini, sudah cukup untuk menggunakan formula yang ditolak sebelum ini:

Rajah 3. Pemfaktoran perbezaan kiub dan ekspresi kota yang luar biasa. Sumber: f. Zapata.

Sekarang, prosedur untuk memohon formula ini terdiri daripada tiga langkah:

- Pertama, akar kubik setiap syarat perbezaan diperolehi.

- Kemudian binomial dan trinomial yang muncul di sebelah kanan formula dibina.

- Akhirnya, binomial dan trinomial diganti untuk mendapatkan pemfaktoran akhir.

Kami akan menggambarkan penggunaan langkah -langkah ini dengan setiap contoh perbezaan kiub yang dicadangkan di atas dan dengan itu memperoleh persamaan yang difokuskan.

Contoh 1

Ekspresi fakta 1 -m⁶   Mengikuti langkah -langkah yang diterangkan. Kami mulakan dengan menulis semula ungkapan sebagai 1 -m⁶ = 1³ - (m²)³ Untuk mengekstrak akar padu masing -masing setiap istilah:

Kemudian binomial dan trinomial dibina:

Ia dapat melayani anda: Teori giliran: sejarah, model, apa itu dan contoh untuk

A = 1

b = m²

Jadi:

A - b = 1 - m²

 (Kepada² +ke.b + b²) = 1² + 1.m² + (m²)² = 1 + m² + m⁴

 Akhirnya ia digantikan dalam formula a³ - b³ = (a-b) (a² +ke.b + b²):

1 -m⁶ = (1 - m²) (1 + m² + m⁴)

Contoh 2

Faktor:

ke⁶b³ -8Z¹²dan⁶ = (a²b)³ - (2Z⁴dan²)³

Oleh kerana ini adalah kiub yang sempurna, akar padu adalah segera: a²B dan 2Z⁴dan², Dari sana ia mengikutinya:

- Binomial: a²B - 2Z⁴dan²

- Trinomial: (a²b)² + ke²b. 2Z⁴dan² + (Kepada²B +2Z⁴dan²)²

 Dan sekarang pemfaktoran yang dikehendaki dibina:

ke⁶b³ -8Z¹²dan⁶ = (a²B - 2Z⁴dan²). [(ke²b)² + ke²b. 2Z⁴dan² + (Kepada²B + 2Z⁴dan²)²] =

= (a²B - 2Z⁴dan²). [ke⁴b² + 2²b.z⁴dan² + (Kepada²B + 2Z⁴dan²)²]

Pada dasarnya pemfaktoran sudah siap, tetapi sering diperlukan untuk mempermudah setiap istilah. Kemudian produk yang luar biasa dibangunkan dari jumlah - yang muncul pada akhir dan kemudian menambah istilah yang serupa. Ingat bahawa kuadrat jumlahnya adalah:

(x + y)² = x² + 2xy + dan²

Hak yang ketara ke kanan berkembang dengan cara ini:

(Kepada²B + 2Z⁴dan²)² = a⁴b² + Ke -4²b.z⁴dan² + 4z⁸dan⁴

 Menggantikan perkembangan yang diperolehi dalam pemfaktoran perbezaan kiub:

ke⁶b³ -8Z¹²dan⁶ = (a²B - 2Z⁴dan²). [ke⁴b² + 2²b.z⁴dan² + ke⁴b² + Ke -4²b.z⁴dan² + 4z⁸dan⁴] =

Akhirnya, mengumpulkan istilah yang sama dan pemfaktoran pekali berangka, yang semuanya berpasangan, diperolehi:

(Kepada²B - 2Z⁴dan²). [2nd⁴b² + 6th²b.z⁴dan² + 4z⁸dan⁴] = 2 (a²B - 2Z⁴dan²). [ke⁴b² + Ke -3²b.z⁴dan² + 2Z⁸dan⁴]

Contoh 3

Faktor (1/125).x⁶  - 27y⁹ Jauh lebih mudah daripada kes sebelumnya. Pertama, setara A dan B dikenalpasti:

A = (1/5) x²

B = 3y³

Kemudian mereka digantikan secara langsung pada formula:

(1/125).x⁶  - 27y⁹ = [(1/5) x² - 3y³]. [(1/25) x⁴ + (3/5) x²dan³ + 9y⁶]

Latihan diselesaikan

Perbezaan kiub mempunyai, seperti yang telah kita katakan, pelbagai aplikasi dalam algebra. Mari lihat beberapa:

Boleh melayani anda: 5 ciri pesawat Cartesian

Latihan 1

Selesaikan persamaan berikut:

a) x⁵ - 125 x² = 0

b) 64 - 729 x³ = 0

Penyelesaian kepada

Pertama persamaan adalah faktor dengan cara ini:

x² (x³ - 125) = 0

Sebagai 125 adalah kiub yang sempurna, kurungan ditulis sebagai perbezaan dalam kiub:

x² . (x³ - 5³) = 0

Penyelesaian pertama ialah x = 0, tetapi kita dapati lebih banyak jika kita membuat x³ - 5³ = 0, kemudian:

x³ = 5³ → x = 5

Penyelesaian b

Bahagian kiri persamaan ditulis semula sebagai 64 - 729 x³ = 4³ - (9x)³. Oleh itu:

4³ - (9x)³ = 0

Oleh kerana eksponen adalah sama:

9x = 4 → x = 9/4

Latihan 2

Faktor ungkapan:

(x + y)³ - (X - y)³

Penyelesaian

Ungkapan ini adalah perbezaan dalam kiub, jika dalam formula pemfaktoran kita perhatikan bahawa:

A = x+ dan

b = x- y

Kemudian binomial dibina terlebih dahulu:

a - b = x+ y - (x- y) = 2y

Dan sekarang trinomial:

ke² + ke.b + b² = (x+ y)² + (x + y) (x-y) + (x-y)²

Produk terkenal dibangunkan:

(x+ y)² = x² + 2xy +dan²

(x+y) (x-y) = x²- dan²

(x- y)² = x² - 2xy +dan²

Kemudian anda perlu menggantikan dan mengurangkan istilah yang serupa:

ke² + ke.b + b² = x² + 2xy +dan²+ x²- dan²+ x² - 2xy +dan² = 3x² + dan²

Faktorisasi menghasilkan:

(x + y)³ - (X - y)³ = 2y. (3x² + dan²)

Rujukan

1. Baldor, a. 1974. Algebra. Editorial kebudayaan Venezuela.Ke.
2. Yayasan CK-12. Jumlah dan perbezaan kiub. Pulih dari: ck12.org.
3. Akademi Khan. Pemfaktoran perbezaan kiub. Pulih dari: Adakah.Khanacademy.org.
4. Matematik menyeronokkan maju. Perbezaan dua kiub. Pulih dari: MathSisfun.com
5. Unam. Pemfaktoran perbezaan kiub. Diperolehi dari: DCB.Fi-c.Unam.mx.