Perbezaan antara bulatan dan lilitan (dengan contoh)

The Perbezaan antara bulatan dan lilitan Ini adalah yang berikut: bulatan adalah permukaan rata, berkontur atau dibatasi oleh bulatan, sementara yang terakhir adalah lengkung rata.

Lazimnya kedua -dua konsep keliru, kerana ia berkaitan, tetapi anda selalu ingat bahawa lilitan adalah tepi bulatan, sementara ia mengandungi lilitan dan semua titik pedalaman.

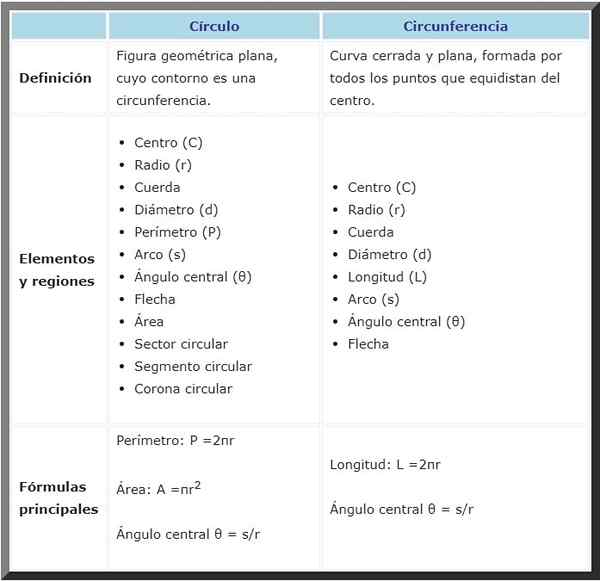
Kedua -duanya mempunyai banyak elemen yang sama, seperti pusat, radius dan diameter, antara lain, mengikut jadual perbandingan berikut:

	Bulatan	Lilitan
Definisi	Angka geometri rata, yang konturnya adalah lilitan.	Lengkung tertutup dan rata, dibentuk oleh semua mata yang sama di tengah.
Unsur dan Kawasan	Pusat (c) Radio (r) Tali Diameter (d) Perimeter (p) Arka (s) Sudut pusat (Θ) Anak panah Kawasan Sektor Pekeliling Segmen bulat Mahkota bulat	Pusat (c) Radio (r) Tali Diameter (d) Panjang (l) Arka (s) Panjang Pusat (Θ) Anak panah
Formula	Perimeter: p = 2π⋅r Kawasan: A =πR2 Sudut Tengah: Θ= s/r	Panjang: L = 2π⋅r Sudut Tengah: Θ= s/r

[TOC]

Bulatan: Definisi, Ciri dan Bahagian

Bulatan adalah angka geometri rata, yang merangkumi semua titik lilitan yang membentuk kontur dan juga semua titik pedalaman.

Atas sebab ini ia dicirikan dengan mempunyai:

-Tepi atau perimeter, iaitu lilitan bulatan.

-Kawasan cetek.

Unsur -unsur bulatan

Setiap bulatan mempunyai bahagian atau elemen berikut:

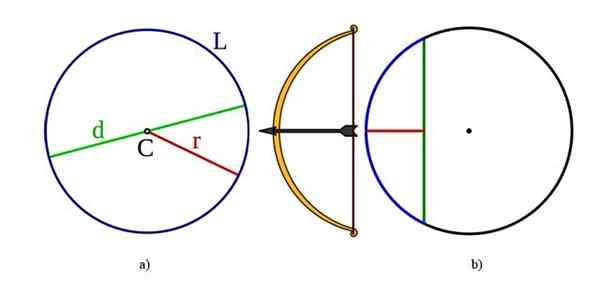Unsur -unsur bulatan, juga biasa dengan lilitan: ke kiri dalam a) adalah pusat d, diameter d, radius r dan panjang l l. Betul -betul di b) ada tali dan sagita atau anak panah. Sumber: Wikimedia Commons.

Pusat: Apa itu titik c, yang sama dengan semua titik di tepi.

Boleh melayani anda: arka (geometri): ukuran, jenis gerbang, contoh

Tali: segmen yang menyertai dua titik tepi bulatan. Dalam angka b) di sebelah kanan, ia adalah segmen hijau yang lebih gelap.

Diameter: segmen hijau yang lebih ringan, dilambangkan "d" dalam angka a), yang menyertai dua titik tepi dan pada masa yang sama melewati pusat. Diameter juga tali, yang paling lama, jadi ia dikenali sebagai Tali utama.

Radio: dilambangkan oleh "r" dalam angka a), ia adalah segmen merah yang bergabung dengan pusat bulatan dengan titik tepi. Ukurannya adalah separuh diameter.

Tunduk: Sebahagian daripada kontur yang antara dua titik ini, dalam warna biru dalam angka b).

Sudut pusat: Ia adalah sudut yang puncaknya berada di tengah atau dan sisi radio bulatan.

Anak panah: segmen tegak lurus ke tali (merah dalam angka b), yang bergabung dengan pusat tali dengan titik tepi.

Panjang atau perimeter: Ia adalah ukuran kontur bulatan, dilambangkan l. Ia bergantung kepada radio r dan berkadar dengan nombor ujung π:

π = 3.1416 ..

Jadi itu:

L = 2π ⋅ r

Kawasan bulat

Menjadi tokoh rata, bulatan mempunyai kawasan keseluruhan dan juga pelbagai wilayah. Yang paling terkenal adalah berikut:

Kawasan bulatan: Ia berkadar dengan kuadrat jejari, pemalar berkadar menjadi nombor π.

Memanggil kawasan bulatan, ia dinyatakan sebagai:

A = πr²

Segmen bulat: Ia adalah sebahagian daripada bulatan yang terhad oleh arka biru dan tali hijau gelap dalam angka b.

Boleh melayani anda: Sudut Tambahan: Apa, Pengiraan, Contoh, Latihan

Sektor Pekeliling: Ia juga merupakan kawasan bulatan, tetapi terkandung di antara dua radio dan lengkungan yang sepadan.

Mahkota bulat: Ia berbentuk seperti cincin dan dibatasi oleh dua lilitan sepusat, di luar radio menor dan di dalam walikota radio.

Lingkaran: dEfinition, ciri dan bahagian 

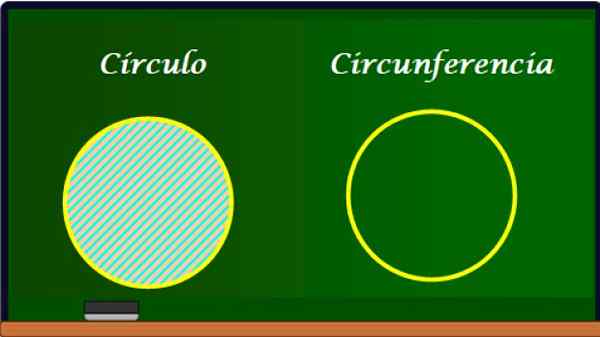Bulatan dan lilitannya. Sumber: f. Zapata.

Lingkaran adalah pinggir bulatan dan oleh itu mempunyai banyak elemen yang sama dengan ini. Walau bagaimanapun, lilitan tidak mempunyai kawasan, kerana kerana ia adalah lengkung ia hanya mempunyai panjang l.

Lilitan secara rasmi ditakrifkan sebagai set semua titik yang disamakan dari titik lain yang dikenali sebagai pusat.

Titik dalaman tidak termasuk, kerana ini sesuai dengan bulatan.

Unsur -unsur lilitan

Banyak unsur -unsur lilitan adalah sama seperti bulatan, tidak termasuk yang merujuk kepada kawasan dan kawasan, jadi angka atas berfungsi sebagai rujukan.

Kami ada:

Pusat: dilambangkan oleh c dan kadang -kadang juga sebagai o, semua titik lilitan menjaga jarak yang sama dengannya.

Tali: segmen yang menyertai dua mata milik lilitan.

Diameter: Ia juga menyertai dua titik lilitan, tetapi selalu melalui pusat yang sama.

Radio: Ia adalah jarak antara pusat dan mana -mana titik lilitan.

Tunduk: Ia adalah sebahagian daripada lilitan.

Sudut pusat: Ia adalah sudut dengan puncak di pusat c dan dua sisi yang sama yang mengukur sama seperti radio.

Anak panah: segmen tegak lurus ke tali, yang bergabung dengan pusat ini dengan titik yang sepadan dengan lilitan.

Boleh melayani anda: Prinsip Multiplicative: Mengira Teknik dan Contoh

Panjang atau perimeter: Ia adalah ukuran lilitan, yang seperti yang kita lihat, adalah berkadar dengan nombor π = 3.1416 ... dan ia dikira oleh formula:

L = 2π ⋅ r

Persamaan lilitan

Titik p milik lilitan selagi jarak ke titik lain c adalah sama dengan r, radio.

Sebarang titik di pesawat Cartesian mempunyai koordinat (X, y) dan persegi jarak d Antara dua daripadanya, p₁(x₁,dan₁) Dan p₂(x₂,dan₂), diberikan oleh formula:

d₂² = (x₂ - x₁)² +  (dan₂ - dan₁)²

Mari kita ambil ke titik koordinat (x, y) dan menyelaraskan titik C (h, k). Menggantikan, persamaan sebelumnya akan seperti ini:

(X - h)² +  (Y- k)² = r²

Ini adalah persamaan lilitan, bahawa apa -apa perkara di atasnya memuaskan. Jika pusat lilitan bertepatan dengan asal -usul sistem koordinat, maka h = k = 0 dan persamaannya dipermudahkan:

x² + dan² = r²

Mari kita lihat contoh cara menggunakan persamaan dan jawab isu ini: Adakah titik (4.6) tergolong dalam lilitan (x - 1)² +  (dan - 2)² = 25?

Untuk mengetahui koordinat titik dalam persamaan diganti, dan jika ia adalah kesamaan, maka titik itu tergolong dalam lilitan:

(4 - 1)² +  (6 - 2)² = 3² + 4² = 9 + 16 = 25

Dan sememangnya, sebagai 25 = 25, disimpulkan bahawa (4.6) adalah milik lilitan.

Rujukan

1. Tutorial Matematik Percuma. Kawasan dan perimeter bulatan - kalkulator geometri. Pulih dari: analisis.com.
2. Rujukan terbuka matematik. Lilitan, perimeter bulatan. Pulih dari: Mathpenref.com.
3. Saintifik. Cara mencari perimeter bulatan. Pulih dari: saintifik.com.
4. Stewart, J. 2006. Preccculment: Matematik untuk Pengiraan. 5th. Edisi. Pembelajaran Cengage.
5. Zill, d. 1984. Algebra dan trigonometri. McGraw Hill.