Konsep jarak jauh Euclidian, formula, pengiraan, contoh

The Jarak Euclidian Ia adalah nombor positif yang menunjukkan pemisahan yang mempunyai dua mata di ruang di mana aksioma dan teorem geometri euclid dipenuhi.

Jarak antara dua mata a dan b ruang euclidian adalah panjang vektor Ab Kepunyaan satu -satunya baris yang melewati perkara -perkara ini.

Rajah 1 . Ruang Euclidean Unidimensional Dibentuk oleh Line (Ox). Beberapa perkara di ruang ini, koordinat dan jarak mereka ditunjukkan. (Disediakan oleh Ricardo Pérez).

Ruang yang kita perhatikan dan di mana kita memindahkan manusia adalah ruang tiga dimensi (3-D), di mana aksioma dan teorem geometri euclide dipenuhi. Di ruang ini terdapat subspace dua dimensi (rancangan) dan satu -dimensi (lurus) (lurus) subspaces.

Ruang Euclidean boleh menjadi satu dimensi (1-D), dua dimensi (2-D), tiga dimensi (3-D) atau N dimensi (N-D).

Ini adalah titik di ruang satu -dimensi x yang tergolong dalam garis berorientasikan (lembu), arah dari atau ke x adalah alamat positif. Untuk mencari titik di baris ini, sistem Cartesian yang terdiri daripada memberikan setiap titik garis digunakan nombor.

[TOC]

Formula

Jarak Euclidian d (a, b) ditakrifkan di antara titik a dan b, yang terletak pada garis, seperti akar kuadrat kuadrat perbezaan koordinat xnya:

D (a, b) = √ ((xb - xa)^2)

Definisi ini menjamin bahawa: Jarak antara dua mata selalu menjadi jumlah positif. Dan bahawa jarak antara a dan b adalah sama dengan jarak antara b dan a.

Rajah 1 menunjukkan ruang Euclidian satu -dimensi yang dibentuk oleh garis (lembu) dan beberapa mata pada baris itu. Setiap titik mempunyai koordinat:

Titik a mempunyai koordinat xa = 2.5, B koordinat xb = 4 dan titik c koordinat xc = -2.5

Ia boleh melayani anda: kebarangkalian kekerapan: konsep, bagaimana ia dikira dan contohnya

D (a, b) = √ ((4 - 2.5) 2) = 1.5

D (b, a) = √ ((2.5 - 4) 2) = 1.5

D (a, c) = √ ((-2.5 - 2.5) 2) = 5.0

Jarak Euclidian dalam dua dimensi

Ruang Euclide dua dimensi adalah pesawat. Titik pesawat Euclidian memenuhi aksioma geometri Euclid, sebagai contoh:

- Pada dua mata satu baris berlalu. 

- Tiga mata di atas kapal terbang membentuk segitiga yang sudut dalamannya selalu menambah 180º.

- Dalam segitiga segi empat tepat, persegi hipotenus sama dengan jumlah kuadrat kakinya.

Dalam dua dimensi satu titik mempunyai koordinat x dan y. 

Contohnya titik P mempunyai koordinat (XP, YP) ​​dan titik yang diselaraskan (XQ, YQ).

Jarak Euclidean antara titik P dan Q ditakrifkan dengan formula berikut:

D (p, q) = √ ((xq - xp)^2 + (yq - yp)^2)

Harus diingat bahawa formula ini bersamaan dengan teorem Pythagoras, seperti yang ditunjukkan dalam Rajah 2.

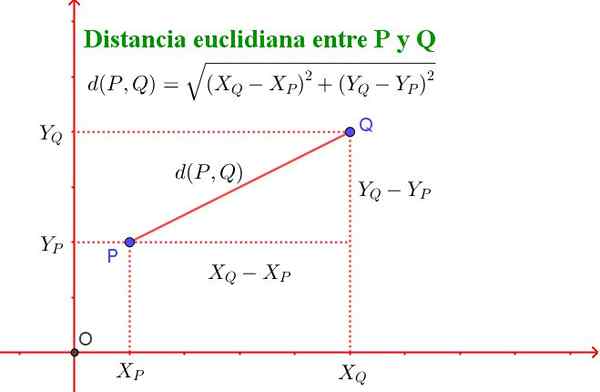Rajah 2. Jarak antara dua titik p dan q pesawat memenuhi teorem pythagoras. (Disediakan oleh Ricardo Pérez).

Permukaan nonuclidian

Tidak semua ruang dua dimensi memenuhi geometri Euclidean. Permukaan sfera adalah ruang dua dimensi.

Sudut segitiga di permukaan sfera tidak menambah 180º dan dengan ini teorem Pythagoras tidak dipenuhi, oleh itu permukaan sfera tidak memenuhi aksioma Euclid.

Jarak Euclidian dalam dimensi N

Konsep koordinat boleh diperluaskan ke dimensi yang lebih besar:

- Dalam titik 2-D P mempunyai koordinat (XP, YP)

- Dalam 3-D titik yang mempunyai koordinat (XQ, YQ, ZQ)

- Dalam 4-D Point R akan mempunyai koordinat (XR, YR, ZR, WR)

- Di N-D A Point P akan mempunyai koordinat (P1, P2, P3, ..., PN)

Boleh melayani anda: bar graf: ciri, apa itu, contohnya

Jarak antara dua titik P dan Q dari ruang Euclidian N-dimensi dikira dengan formula berikut:

D (p, q) = √ ((q1 - p1)^2 +(q2 - p2)^2 +... +(qn - pn)^2)

Tempat geometri dari semua titik yang dalam ruang Euclidean n-dimensi yang sama dengan Equidists dari titik p tetap (pusat) yang lain membentuk hipersfera n-dimensi.

Cara Mengira Jarak Euclidian

Berikut adalah jarak antara dua titik yang terletak di ruang tiga dimensi Euclidian dikira.

Anggap Titik A Koordinat Cartesian X, Y, Z yang diberikan oleh A :( 2, 3, 1) dan titik B koordinat b :( -3, 2, 2).

Anda ingin menentukan jarak antara titik -titik ini, yang mana hubungan umum digunakan:

D (a, b) = √ ((-3 - 2) 2 + (2 - 3) 2 + (2 - 1) 2) = √ ((-5) 2 + (-1) 2 + (1) 2 )

D (a, b) = √ (25 + 1 + 1) = √ (27) = √ (9 *3) = 3 √ (3) = 5.196

Contoh

Terdapat dua mata p dan q.  Titik P untuk Koordinat Cartesian x, y, z yang diberikan oleh p :( 2, 3, 1) dan titik q koordinat Q :( -3, 2, 1).

Diminta untuk mencari koordinat titik tengah m dari segmen [PQ] yang menghubungkan dua mata. 

Penyelesaian:

Diandaikan bahawa titik mknown m mempunyai koordinat (x, y, z).

Oleh kerana m adalah titik purata [pq] ia mesti dipenuhi bahawa d (p, m) = d (q, m), jadi ia juga harus dipenuhi d (p, m)^2 = d (q, m)^ 2:

(X - 2)^2 + (y - 3)^2 + (z - 1)^2 = (x - (-3))^2 + (y - 2)^2 + (z - 1)^2

Seperti dalam kes ini, istilah ketiga adalah sama dalam kedua -dua ahli ungkapan sebelumnya dipermudahkan untuk:

Dapat melayani anda: pemalar mutlak

(X - 2)^2 + (y - 3)^2 = (x + 3)^2 + (y - 2)^2 

Terdapat persamaan dengan dua tidak diketahui x dan y. Persamaan lain diperlukan untuk menyelesaikan masalah.

Point M tergolong dalam garis yang melewati titik P dan Q, yang boleh kita hitung seperti berikut:

Pertama ialah vektor pengarah Pq garis: Pq = = .

Kemudian P.m = Op + ke Pq, di mana Op Ia adalah kedudukan vektor titik p dan ke Ia adalah parameter yang dimiliki oleh nombor sebenar. 

Persamaan sebelumnya dikenali sebagai persamaan vektor garis, yang dalam koordinat Cartesian mengamalkan seperti berikut:

= + A =

Sama dengan komponen yang sepadan ialah:

X - 2 = 2 - 5 a; Dan - 3 = 3 -a; Z - 1 = 0

Iaitu x = 4 - 5a, y = 6 - a, akhirnya z = 1.

Ia digantikan dalam ungkapan kuadratik yang berkaitan dengan x ke y:

(4 - 5a - 2)^2 + (6 - a - 3)^2 = (4 - 5a + 3)^2 + (6 - a - 2)^2

Ia dipermudahkan:

(2 - 5a)^2 + (3 -a)^2 = (7 - 5a)^2 + (4 - a)^2

Kini berkembang:

4 + 25 a^2 - 20a + 9 + a^2 - 6a = 49 + 25 a^2 - 70a + 16 + a^2 - 8a

Ia dipermudahkan, membatalkan istilah yang sama dalam kedua -dua ahli:

4 - 20a + 9 - 6a = 49 - 70a + 16 - 8a

Parameter a:

52 A = 49 + 16 - 4 - 9 = 52 mengakibatkan A = 1.

Iaitu x = 4 - 5, y = 6 - 1, akhirnya z = 1.

Akhirnya kita memperoleh koordinat Cartesian dari titik tengah m segmen [PQ]:

M: (-1, 5, 1).

Rujukan

1. Lehmann c. (1972) Geometri analisis. Uteha.
2. Superprof. Jarak antara dua mata. Pulih dari: superprof.adalah
3. Unam. Jarak antara jenis sublinear yang berkaitan. Pulih dari: prometheus.Matem.Unam.mx/
4. Wikipedia. Jarak Euclidian. Pulih dari: Adakah.Wikipedia.com
5. Wikipedia. Ruang Euclidean. Pulih dari: Adakah.Wikipedia.com