Budaya dan masyarakat umum

Pengagihan eksponen

4708
1366
Horace Gulgowski

Kami menerangkan apakah pengedaran eksponen, ciri -ciri, formula, contoh dan latihan yang diselesaikan

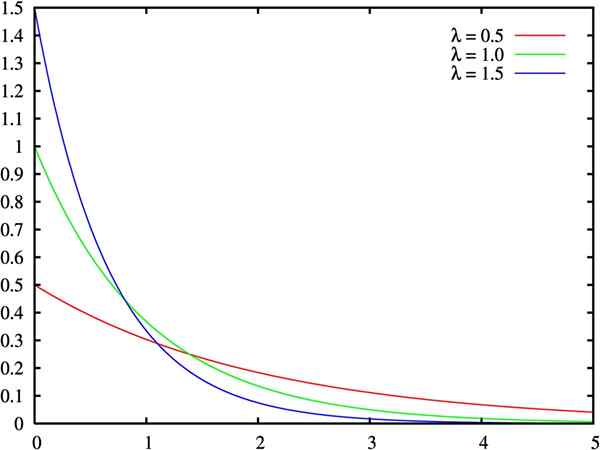
Grafik fungsi ketumpatan pengedaran eksponen, untuk tiga nilai parameter lambda. Sumber: Wikimedia Commons.

Apakah pengedaran eksponen?

The Pengagihan eksponen Ia adalah model probabilistik untuk pembolehubah rawak yang berterusan. Ini bermakna, melalui itu, anda dapat mengetahui kebarangkalian berlakunya nilai tertentu pembolehubah, jadi ia adalah taburan kebarangkalian.

Untuk mendapatkan pengedaran, ia bermula dari a fungsi ketumpatan, yang mempunyai bentuk parameter eksponen λ> 0:

$f(x)=\begincases \lambda e^-\lambda x& \text si x>0 \\ 0 & \ teks Yeah x \ leq 0 \ End kes$

Fungsi ketumpatan seperti itu tidak membenarkan mengira kebarangkalian, tetapi apabila ditubuhkan f (x), fungsi pengedaran f (x), yang mana kebarangkalian diperoleh, diperolehi dengan integrasi f (x). Sebagai contoh, kebarangkalian p bahawa pemboleh ubah rawak mengambil nilai antara 0 dan x adalah:

$F(x)=P[x\leq x]=\int_0^xf(x)dx$

Menjalankan integrasi, yang sangat mudah, kerana integral eksponen adalah eksponen yang sama, kecuali untuk pemalar yang mengiringi hujah, diperolehi:

$F(x)=\int_0^x\lambda e^-\lambda xdx=\lambda \left (-\frac1\lambda \right )\left [ e^-\lambda x \right ]_0^x=-\left (e^-\lambda x-e^0 \right )=1-e^-\lambda x$

Pengagihan eksponen digunakan secara meluas untuk menentukan kebarangkalian peristiwa selepas masa menunggu tertentu, seperti masa yang berlaku dalam kemunculan hospital sebelum pesakit tiba.

Lazimnya, peristiwa merujuk kepada kegagalan atau pecahan jenis elektrik, elektronik dan lain -lain. Dalam kes ini, pengedaran eksponen membantu menganggarkan masa yang diperlukan untuk komponen gagal, dan juga masa antara pembaikan. Ini dikenali sebagai teori kebolehpercayaan.

Ciri -ciri pengedaran eksponen

Beberapa ciri yang paling luar biasa dari fungsi ketumpatan f (x) dari taburan eksponen adalah seperti berikut:

F (x) positif.
Kawasan di bawah lengkung y = f (x) = λe^-Λ^x Ia sentiasa sama dengan 1, kerana jumlah kebarangkalian berlakunya semua nilai pembolehubah mestilah 1. Ini adalah syarat bahawa fungsi ketumpatan memenuhi. Kawasan ini dikira melalui integral:

Boleh melayani anda: anuma

$\int_-\infty ^\infty f(x)dx=\int_-\infty ^\infty \lambda e^-\lambda xdx=1$

Kekurangan ingatan pengedaran eksponen

Ciri yang paling cemerlang dalam pengedaran eksponen adalah kekurangan ingatannya. Sebagai contoh, katakan bahawa masa berlalu sedang memodelkan dengan pengedaran ini sehingga kegagalan unsur berlaku.

Nah, kekurangan ingatan merujuk kepada mengetahui bahawa elemen itu bekerja untuk masa survival "s", tidak mengubahsuai kebarangkalian bahawa elemen akan terus berjalan sehingga jumlah tambahan masa "T".

Ia.

Secara matematik ia dikira dengan definisi kebarangkalian peristiwa bebas:

$P[x\geq s+t/x\geq s]=\fracP[x\geq s+t]P[x\geq s]=\frac1-F(s+t)1-F(s)=\frac1- [1-e^-\lambda (s+t) ]1- [1-e^-\lambda s ]= \beginmatrix \\ \endmatrix$

$=e^-\lambda t$

Oleh itu, kebarangkalian tidak bergantung pada masa s atau kelangsungan hidup.

Formula

1.- Fungsi ketumpatan pengagihan eksponen adalah:

$f(x)=\begincases \lambda e^-\lambda x& \text si x>0 \\ 0 & \ teks Yeah x \ leq 0 \ End kes$

Di mana λ adalah parameter pengedaran.

2.- Seperti yang diterangkan di atas, pengedaran kebarangkalian itu sendiri dilambangkan sebagai f (x) dan kebarangkalian yang berbeza diperolehi dengan integrasi fungsi ketumpatan:

$F(x)=\begincases 0 & \text si x\leq 0 \\ 1-e^-\lambda x& \text si x>0 \ End kes$

3.- Dari yang di atas ia mengikuti bahawa kebarangkalian bahawa pembolehubah mengambil nilai kurang daripada atau sama dengan "x" adalah p [x≤x] = 1 -e^-Λ^x.

4.- Kawasan di bawah lengkung y = f (x), termasuk antara a dan b membolehkan untuk mengira kebarangkalian bahawa pemboleh ubah berada dalam selang [a, b]. Kawasan ini adalah:

P [A ≤ x ≤ b] = f (b) - f (a)

5.- Nilai p [x ≥ a] ialah 1 - f (a) = 1 - (1 - e^-Λ^x) = e^-Λ^x

Nilai yang dijangkakan pengedaran eksponen

Harapan atau nilai yang dijangkakan e (x) pengagihan eksponen adalah nilai yang dijangka berlaku lebih kerap. Ia dikira dari integral:

Boleh melayani anda: Teknik pendaftaran maklumat

$E(x)=\int_0^\infty xf(x)dx$ Yang mudah diselesaikan dengan kaedah integrasi mengikut bahagian. Hasilnya ialah:

E (x) = 1/λ

Varians pengedaran eksponen

Untuk pengiraan varians, integral mesti ditentukan:

$Var(x)=\int_0^\infty x^2f(x)dx$

Yang juga diselesaikan dengan kaedah integrasi oleh bahagian, untuk mendapatkan:

Var (x) = 1/λ²

Khusus pengagihan eksponen adalah bahawa sisihan piawai s (x), yang ditakrifkan sebagai akar kuadrat varians adalah:

S (x) = √var (x) = √ (1/λ²) = 1/λ

Iaitu, sisihan piawai adalah sama dengan harapan pengedaran.

Contoh pengedaran eksponen

Dataran sampel karbon 14

Pengagihan eksponen digunakan untuk menentukan masa yang diperlukan untuk hancur zarah radioaktif. Masa -masa ini digunakan untuk tarikh sampel fosil oleh radiokarbon.

Masa yang diperlukan untuk memeriksa surat

Anda boleh memodelkan masa pengguna untuk menyemak e -mel mereka, sebaik sahaja pemberitahuan telah diterima, melalui pengedaran eksponen. Katakan parameter pengedaran ialah λ = 0.2 Oleh itu, kebarangkalian bahawa seseorang mengambil masa kurang dari 1 minit untuk mengkaji e -melnya adalah:

$P[x\leq 1]=\int_0^1f(x)dx=\int_0^10.2e^-0.2xdx$

Integral ini diselesaikan pada mulanya, ia hanya kekal untuk menggantikan nilai berangka dalam penyelesaian dan mengira hasil akhir:

P [x ≤ 1] = 1 --e^-^0.2^×¹ = 1- e^-^0.2 = 1- 0.819 = 0.181

Ia juga boleh diganti secara langsung pada fungsi f (x) yang diberikan di atas, untuk mendapatkan f (1).

Latihan

Latihan 1

Cari kebarangkalian bahawa seseorang kemudian satu jam mengkaji e -mel mereka, jika taburan kebarangkalian adalah eksponen, dengan parameter λ = 0.2.

Penyelesaian

P [x ≥ 60] mesti dikira, kerana 1 jam bersamaan dengan 60 minit dan kebarangkalian orang itu lewat 60 minit atau lebih untuk memeriksa surat yang diminta. Kebarangkalian dikira dengan integral yang sama yang dibentangkan pada mulanya, hanya mengubah had integrasi:

Boleh melayani anda: rapa nui: sejarah, ciri, budaya, tradisi

$P[x\geq 60]=\int_60^\infty 0.2e^-0.2xdx=-\left ( -e^-0.2\times 60 \right )=0.000006144$

Nilai yang diperoleh adalah kecil, jadi sangat tidak mungkin seseorang mengambil masa lebih dari satu jam untuk menyemak e -mel mereka.

Latihan 2

Mentol elektrik biasanya mempunyai tempoh yang terhingga, kecuali mentol terkenal di stesen bomba di Livermore, California, yang tidak pernah gagal sejak pertama kali, pada tahun 1901.

Anggapkan bahawa tempoh mentol semasa mengikuti taburan eksponen, dengan nilai yang dijangkakan selama 8 bulan. Kira:

a) Apakah kebarangkalian mentol akan berlangsung antara 5 dan 14 bulan?

b) Kebarangkalian bahawa mentol akan bertahan lebih dari 25 bulan, mengetahui bahawa ia mempunyai lebih dari 11 bulan beroperasi.

Penyelesaian kepada

Perkara pertama adalah mencari nilai λ, melalui nilai yang dijangkakan pengedaran e (x) = 8 bulan. Mengikut apa yang dikatakan di bahagian sebelumnya, nilai yang dijangkakan adalah kebalikan dari parameter λ, oleh itu:

E (x) = 1 /λ → λ = 1 /e (x) = 1/8 = 0.125

Kemudian kebarangkalian yang diminta dikira, melalui integral yang diberikan pada mulanya, tetapi mudah mengubah had integrasi:

Kemudian ia digantikan dalam fungsi F (x) yang diberikan dalam bahagian sebelumnya, seperti berikut:

P [5 ≤ x ≤ 14] = f (14) - f (5) = [1 - e^{-(0.125 × 14)}] - [1 - e^{-(0.125 × 5)}] = 0.36

Penyelesaian b

Untuk menjawab isu ini, harta kekurangan ingatan akan digunakan, dinyatakan di atas. Seperti yang diketahui bahawa ia telah berlangsung lebih dari 11 bulan, maka:

S = 11 bulan

Masa tambahan hingga 25 bulan atau lebih adalah:

T = 14 bulan

P [x ≥ s + t│t ≥ s] = p [x ≥ 11 + 14 ≥ 11] = e^{-0.125 × 14}= 0.174