Pengagihan diskret
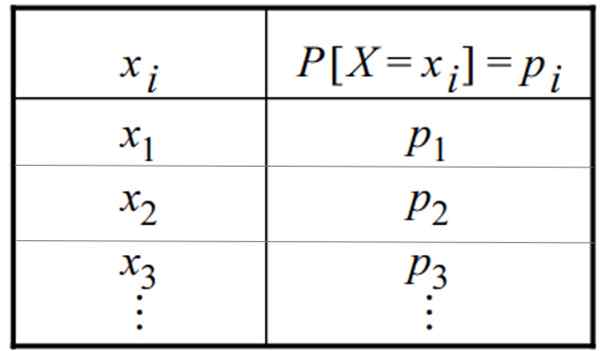
- 3831
- 571
- Anthony Breitenberg
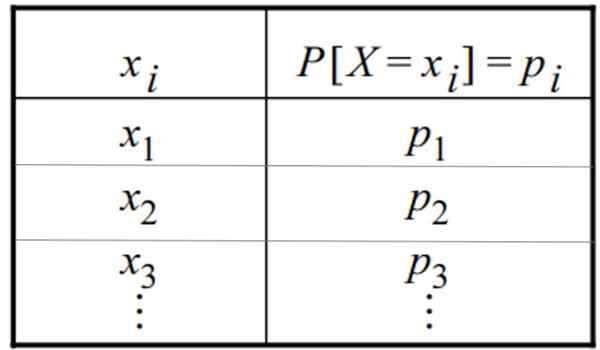 Jadual pengagihan kebarangkalian yang bijak. Sumber: f. Zapata
Jadual pengagihan kebarangkalian yang bijak. Sumber: f. Zapata Apa itu pengagihan yang bijak?
A pengedaran bijak kebarangkalian adalah fungsi f (xYo) yang menyerahkan kepada setiap nilai pemboleh ubah diskret: x1, x2, x3,... xYo, Kejadian kejadian P (x = xYo). Fungsi ini juga dikenali sebagai "Fungsi Massa Kebarangkalian".
Pengagihan kebarangkalian diskret dapat diberikan dalam bentuk jadual atau grafik. Jadual mempunyai bentuk umum ini, di mana pembolehubah muncul dalam satu lajur dan kebarangkalian masing -masing di sisi lain:
Fungsi Massa Kebarangkalian berkongsi ciri -ciri umum berikut:
- Kebarangkalian pYo mana -mana acara xYo Ia adalah antara 0 dan 1, walaupun beberapa nilai had ini: 0 ≤ x ≤ 1.
- P (x = xYo) = pYo Hanya ambil nilai positif, oleh itu: p (x = xYo) ≥ 0.
- Memang benar bahawa Σ p (xYo) = 1 untuk semua kemungkinan nilai x.
Pengagihan kebarangkalian menggambarkan tingkah laku populasi, yang diterangkan oleh parameternya: purata μ, varians σ2 dan sisihan piawai s = σ σ2.
Seterusnya, pengagihan diskret yang paling ketara dijelaskan secara ringkas:
Pengagihan seragam
Ia adalah pengagihan yang paling sederhana dari semua. Di dalamnya pemboleh ubah boleh mengambil nilai diskret "n": x1, x2, x3,... xYo, Semua dengan kebarangkalian yang sama. Dalam kes ini, pengedaran diberikan oleh:
Pengagihan binomial
Ia terpakai kepada pengalaman dengan hanya dua hasil yang mungkin dan saling eksklusif, yang biasanya dipanggil "kejayaan" dan "kegagalan", dilambangkan sebagai E dan F masing -masing. Hakikat bahawa peristiwa dipanggil "kejayaan," tidak semestinya bermaksud bahawa ia adalah perkara yang baik, ia adalah sebilangan besar yang sewenang -wenangnya.
Kebarangkalian kejayaan p (e) dalam latihan "n", dilambangkan sebagai p, dan kegagalan p (f) seperti q = 1 - p.
Jika "x" mewakili sejumlah kejayaan dalam ujian bebas "n", memang benar bahawa: 0 ≤ x ≤ n. Dan kebarangkalian kejadian p (x) peristiwa dikira melalui formula berikut:
Ia boleh melayani anda: sentimeter persegi hingga meter persegi (cm² hingga m²)Di mana x = 0, 1, 2, 3 ..., n dan simbol (!) bermaksud "faktorial":
x! = x ∙ (x - 1) ∙ (x - 2) ∙ (x - 3) ... 1
0! = 1
Pengagihan Poisson
Dalam pengedaran ini, pembolehubah rawak x menunjukkan berapa kali peristiwa berlaku dalam beberapa selang, yang boleh menjadi masa, jarak atau lain -lain. Kejadian peristiwa adalah rawak, bebas dan diedarkan secara merata sepanjang selang waktu yang dipersoalkan.
Sebaik sahaja keadaan ini, kebarangkalian, yang bergantung kepada purata μ kejadian dan bilangan euler atau nombor "E", dikira oleh:
Peluang peristiwa dengan pengedaran ini kecil, jadi ia dipanggil "undang -undang kes yang jarang berlaku".
Pendekatan pengedaran binomial
Pengagihan Poisson berfungsi sebagai pendekatan kepada pengedaran binomial apabila n adalah besar (n≥ 100) dan p adalah kecil (np ≤ 10). Dalam kes ini, purata μ dikira sebagai:
μ = n ∙ p
Pengagihan Hypergeometric
Ia digunakan apabila kebarangkalian tidak bebas, iaitu, setelah menjalankan eksperimen, syarat -syarat tidak sama lagi. Inilah yang berlaku apabila mengekstrak sampel tanpa pengganti dari populasi, jadi pengedaran binomial tidak lagi boleh digunakan.
Jika populasi terdiri daripada dua jenis objek yang berbeza dari dan b, dan pada objek rawak dan tanpa penggantian, kebarangkalian mendapatkan objek X jenis A adalah:
Di mana a dan b adalah jumlah objek masing -masing jenis, hadir dalam populasi.
Walau bagaimanapun, jika penduduknya sangat besar, walaupun tidak ada penggantian, sukar bagi elemen yang sama untuk dipilih lebih dari sekali, jadi kedua -dua pengedaran: binomial dan hypergeometric, menghasilkan hasil yang sama.
Boleh melayani anda: Perbezaan kiub: formula, persamaan, contoh, latihanContoh
Duit syiling dilancarkan
Co -launches adalah contoh yang sangat ilustrasi:
-Pelancaran mata wang yang jujur, dan mendapat wajah. Diketahui bahawa wajah 1 mempunyai ½ kebarangkalian meninggalkan dan salib (0 muka), sama. Pengagihan ditunjukkan dalam jadual ini:
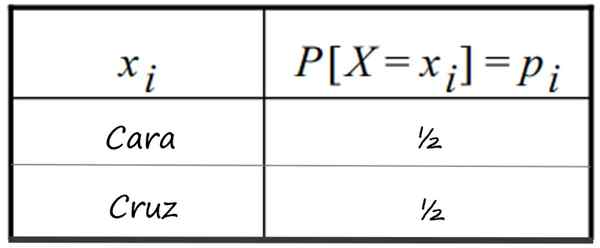 Jadual pengedaran kebarangkalian diskret yang mengikuti pelancaran 1 mata wang jujur. Sumber: f. Zapata
Jadual pengedaran kebarangkalian diskret yang mengikuti pelancaran 1 mata wang jujur. Sumber: f. Zapata -Pukulan serentak dari dua duit syiling yang jujur dan kemungkinan bilangan muka yang boleh diperolehi.
 Jadual pengedaran kebarangkalian diskret yang mengikuti pelancaran dua mata wang yang jujur, dengan tujuan untuk mendapatkan wajah atau tidak. Sumber: f. Zapata
Jadual pengedaran kebarangkalian diskret yang mengikuti pelancaran dua mata wang yang jujur, dengan tujuan untuk mendapatkan wajah atau tidak. Sumber: f. Zapata Pembolehubah dengan pengedaran seragam
-Pemilihan nombor integer yang sama atau ganjil: masing -masing adalah kebarangkalian sama dengan ½ dipilih dalam set nombor keseluruhan.
-Pelancaran dadu yang jujur. Dalam kes ini terdapat 6 muka bernombor dan masing -masing mempunyai kebarangkalian yang sama meninggalkan: 1/6.
-Pemilihan topik untuk mengambil peperiksaan, dipilih dari antara isu n, jika semuanya mungkin mungkin.
Pembolehubah dengan pengedaran binomial
-Bilangan wajah yang keluar dengan melancarkan duit syiling yang jujur.
-Daripada penduduk 250 keluarga, jumlah ini yang mempunyai 2 orang anak.
-Jumlah rosewoods yang bertahan, selepas tukang kebun 20 rosales di taman.
-Kajian dengan 50 pesakit, bilangan mereka yang membentangkan tindak balas negatif terhadap ubat.
-Bilangan pelajar yang diluluskan dalam peperiksaan kebarangkalian, kumpulan yang terdiri daripada 100 pelajar.
Pembolehubah dengan pengedaran Poisson
-Bilangan panggilan seminit ke Pusat panggilan Syarikat.
-Bilangan gempa bumi besar setiap tahun untuk kawasan geografi tertentu.
-Jumlah tornado yang mempengaruhi rantau tertentu pada tahun lepas.
-Bilangan pokok yang dijangkiti kulat, satu hektar persegi hutan.
Pembolehubah dengan pengedaran hypergeometric
-Kejayaan nombor atau kombinasi memenangi perjudian.
Boleh melayani anda: vektor serentak: ciri, contoh dan latihan-Pemilihan sejumlah perempuan atau lelaki dalam sampel ikan N ikan ikan.
Latihan yang diselesaikan
Latihan 1
Kajian yang ditentukan oleh orang dewasa yang secara rawak yang mempunyai telefon pintar, 54% daripadanya menggunakannya di kelas atau mesyuarat. Anda ingin mencari kebarangkalian bahawa, secara rawak memilih 8 orang dengan telefon pintar, betul -betul 6 daripadanya menggunakannya di kelas atau mesyuarat.
Penyelesaian
Eksperimen ini bersetuju dengan percubaan binomial, kerana hasilnya adalah binari: seseorang mengambil telefon di kelas atau tidak mengeluarkannya. Hakikat bahawa orang yang menggunakan telefon berada di kelas boleh dipanggil kejayaan, dan kegagalan jika tidak (sebelum dijelaskan bahawa pilihan ini benar -benar sewenang -wenangnya).
Dalam kes itu: p = 0.54 dan q = 1- 0.54 = 0.46.
Oleh kerana 8 orang dipilih secara rawak, maka n = 8 dan nilai x adalah 6, oleh itu, nilai yang diperlukan tersedia untuk menggantikannya dalam formula pengedaran binomial:
Latihan 2
Untuk tahun baru -baru ini, klinik mendaftarkan 4221 kelahiran. Dengan data unik ini, tentukan kebarangkalian bahawa terdapat 15 kelahiran dalam 1 hari. Adakah acara ini jarang berlaku?
Penyelesaian
Pengagihan Poisson digunakan, seperti yang diminta untuk menentukan kebarangkalian kejadian kejadian yang berlaku dalam selang waktu. Dalam kes ini, pemboleh ubah adalah jumlah kelahiran dan selangnya adalah 1 hari.
Formula pengedaran Poisson memerlukan kelahiran purata setiap hari, yang mudah dikira:
Oleh itu, kebarangkalian x = 15 kelahiran/hari adalah:
Hasilnya dapat dinyatakan dari segi peratusan untuk kejelasan: 6.42% mungkin bahawa, pada bila -bila masa, betul -betul 15 kelahiran berlaku. Acara ini tidak mungkin, walaupun tidak mustahil.


=\frac1n)
=\fracn!\left&space;(&space;n-x&space;\right&space;)!\cdot&space;x!\cdot\:p^x\cdot&space;q^n-x)
=\frac\mu&space;^x\cdot&space;e^-\mu&space;x!)
=\fracA!\left&space;(A-x&space;\right&space;)!\cdot&space;x!\cdot&space;\fracB!\left&space;(B-n+x&space;\right&space;)!\cdot&space;\left&space;(n-x&space;\right&space;)!\div&space;\frac\left&space;(A+B&space;\right&space;)!\left&space;(A+B-n&space;\right&space;)!\cdot&space;n!)
=\frac8!\left&space;(8-6&space;\right&space;)!\times&space;6!\times&space;0.54^6\times&space;0.46^\left&space;(8-6&space;\right&space;)=\frac8!2!\times&space;6!\times&space;0.54^6\times&space;0.46^2=0.147)

=\frac11.56^15\times&space;e^-11.5615!=0.0642)