Bahagian sintetik

Kami menerangkan apa bahagian sintetik, kaedah untuk melakukannya, contoh dan latihan diselesaikan.

Apakah bahagian sintetik?

The Bahagian sintetik Ini adalah cara mudah untuk membahagikan polinomial p (x) dengan salah satu bentuk d (x) = x - c - c. Sebagai contoh, polinomial p (x) = (x⁵+3x⁴-7x³+2x²-8x+1) Ia boleh diwakili sebagai pendaraban dua polinomial paling mudah (x+1) dan (x⁴ + 2x³).

Ini adalah alat yang sangat berguna, kerana, sebagai tambahan kepada kita untuk membahagikan polinomial, ia juga membolehkan untuk menilai polinomial P (x) dalam mana -mana nombor C, yang seterusnya menunjukkan kita tepat jika nombor itu adalah sifar atau tidak dari polinomial.

Terima kasih kepada algoritma bahagian, kita tahu bahawa jika kita mempunyai dua P (x) dan d (x) polinomial (x) + r (x), di mana r (x) adalah sifar atau kurang daripada q (x). Polinomial ini dikenali sebagai kuota dan sisa atau rehat, masing -masing.

Pada masa -masa di mana polinomial d (x) adalah bentuk x - c, bahagian sintetik memberi kita cara yang singkat untuk mencari siapa q (x) dan r (x).

Kaedah pembahagian sintetik

Biarkan p (x) = a_nxⁿ+ke_N-1x^N-1+... +a₁x+a₀ polinomial yang kita mahu membahagikan dan d (x) = x-c pembahagi. Untuk membahagikan kaedah pembahagian sintetik, kami meneruskan seperti berikut:

1- Kami menulis koefisien p (x) pada baris pertama. Sekiranya kuasa x tidak muncul, kami meletakkan sifar sebagai pekalinya.

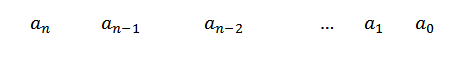
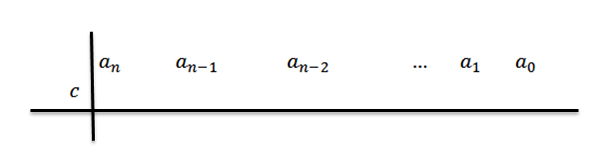
2- di barisan kedua, di sebelah kiri a_n Kami meletakkan C, dan menarik garis bahagian, seperti yang ditunjukkan dalam angka berikut:

3- Kami menurunkan pekali terkemuka ke barisan ketiga.

Boleh melayani anda: Kaedah Euler: Apakah penggunaan prosedur dan latihan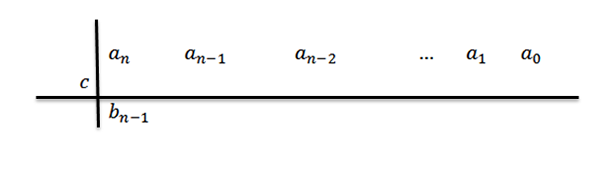

Dalam ungkapan ini b_N-1= a_n

4- Kami melipatgandakan C oleh pekali terkemuka b_N-1 Dan kami menulis hasilnya di barisan kedua, tetapi lajur di sebelah kanan.

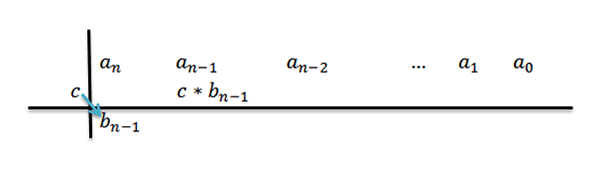
5- Kami menambah lajur di mana kami menulis hasil sebelumnya dan hasilnya diletakkan di bawah jumlah tersebut. Iaitu, dalam lajur yang sama, baris ketiga.

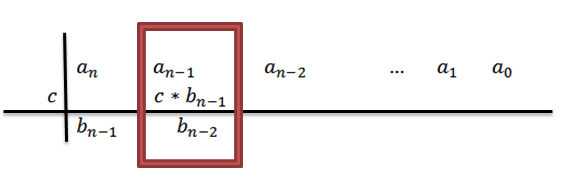
Dengan menambah, kami mempunyai hasilnya_N-1+C*b_N-1, yang mana untuk keselesaan kita akan menghubungi b_N-2

6- Kami melipatgandakan C oleh hasil sebelumnya dan menulis hasilnya ke kanan anda di barisan kedua.

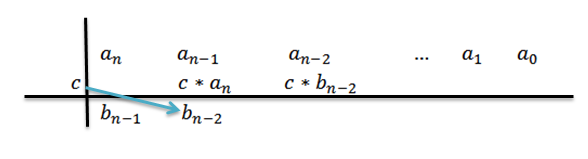
7- Kami mengulangi langkah 5 dan 6 sehingga kita mencapai pekali untuk₀.

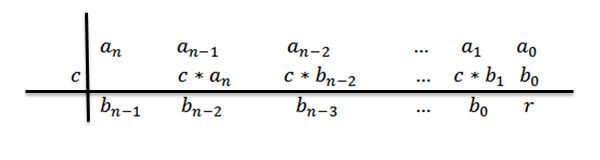
8- Kami menulis jawapannya, iaitu, kuil dan sisa. Seperti yang kita lakukan pembahagian polinomial gred n antara polinomial gred 1, kita mempunyai bahawa quotient akan gred n-1.

Koefisien polinomial kota akan menjadi bilangan baris ketiga, kecuali yang terakhir, yang akan menjadi polinomial sisa atau selebihnya.

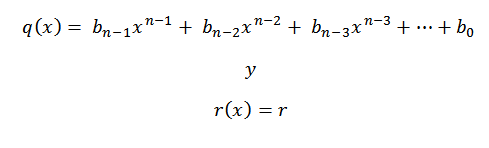
Latihan yang diselesaikan

Contoh 1

Buat bahagian berikut dengan kaedah bahagian sintetik:

(x⁵+3x⁴-7x³+2x²-8x+1): (x+1).

Penyelesaian

Mula -mula kita menulis pekali dividen seperti berikut:

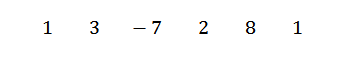
Kemudian kami menulis C di sebelah kiri, di barisan kedua, bersama dengan garis bahagian. Dalam contoh ini c = -1.

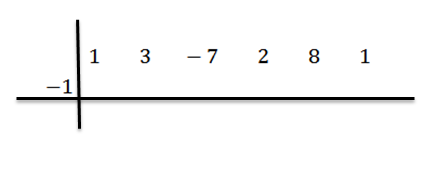
Kami menurunkan pekali terkemuka (dalam kes ini b_N-1 = 1) dan kami membiaknya dengan -1:

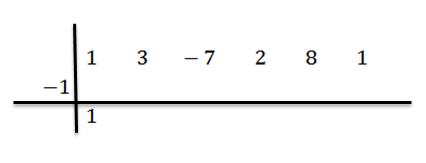
Kami menulis hasilnya ke kanan di barisan kedua, seperti yang ditunjukkan di bawah:

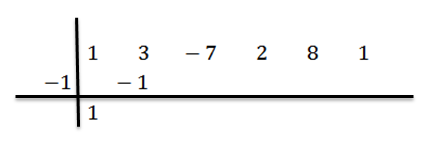
Kami menambah nombor lajur kedua:

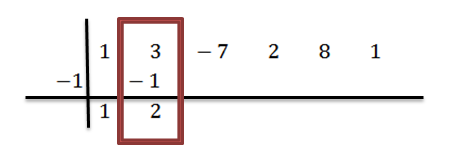
Kami membiak 2 dengan -1 dan menulis hasilnya dalam lajur ketiga, baris kedua:

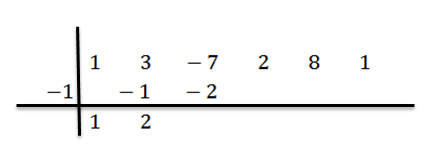
Kami menambah lajur ketiga:

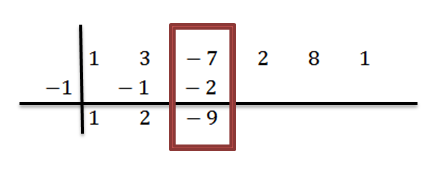
Kami meneruskan analogi sehingga kami mencapai lajur terakhir:

Boleh melayani anda: Pendekatan lalai dan berlebihan: Apakah dan contohnya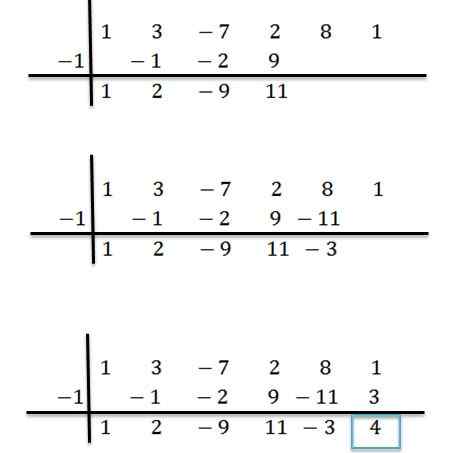

Oleh itu, kita mempunyai nombor terakhir yang diperolehi adalah bahagian lain, dan bilangan baki adalah koefisien polinomial kota. Ini ditulis seperti berikut:

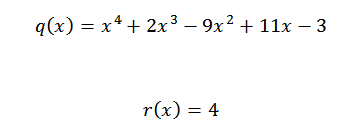
Jika kita ingin mengesahkan bahawa hasilnya betul, sudah cukup untuk mengesahkan bahawa persamaan berikut dipenuhi:

P (x) = q (x)*d (x) + r (x)

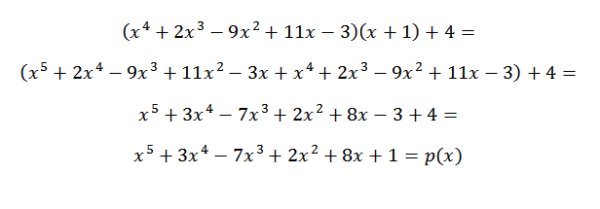
Oleh itu, kita dapat mengesahkan bahawa hasil yang diperoleh adalah betul.

Contoh 2

Lakukan bahagian polinomial berikut dengan kaedah bahagian sintetik:

(7x³-x+2): (x+2)

Penyelesaian

Dalam kes ini kita mempunyai istilah x² Ia tidak muncul, jadi kita akan menulis kepada 0 sebagai pekalinya. Oleh itu, polinomial akan kekal sebagai 7x³+0x²-x+2.

Kami menulis pekali anda berturut -turut, iaitu:

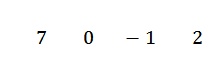
Kami menulis nilai c = -2 ke sebelah kiri di baris kedua dan lukiskan garisan bahagian.

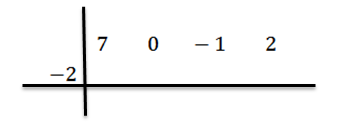
Kami menurunkan pekali terkemuka b_N-1 = 7 dan kami membiaknya dengan -2, menulis hasilnya di barisan kedua ke kanan.

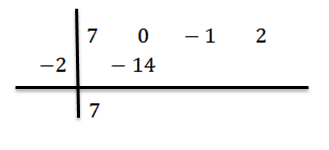
Kami menambah dan meneruskan, seperti yang dijelaskan sebelumnya, sehingga kami mencapai istilah terakhir:

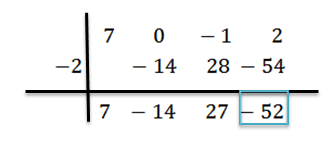
Dalam kes ini, selebihnya ialah r (x) = -52 dan quotient yang diperolehi adalah q (x) = 7x²-14x+27.

Contoh 3

Cara lain untuk menggunakan bahagian sintetik adalah seperti berikut.

Untuk algoritma bahagian, kita boleh menulis polinomial P (x) seperti berikut:

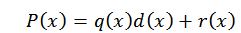
Dalam ungkapan ini, q (x) dan r (x) adalah kuota dan selebihnya. Sekarang, jika d (x) = x-c, ketika menilai dalam c dalam polinomial kita dapati yang berikut:

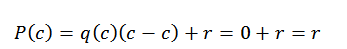
Inilah sebabnya hanya untuk mencari r (x), dan kita boleh melakukan ini terima kasih kepada bahagian sintetik.

Sebagai contoh, kami mempunyai polinomial p (x) = x⁷-9x⁶+19x⁵+12x⁴-3x³+19x²-37x-37 dan kami ingin tahu apa nilainya ketika menilai di x = 5. Untuk ini kita menjalankan pembahagian antara P (x) dan d (x) = x -5 oleh kaedah bahagian sintetik:

Boleh melayani anda: simetri paksi: sifat, contoh dan latihan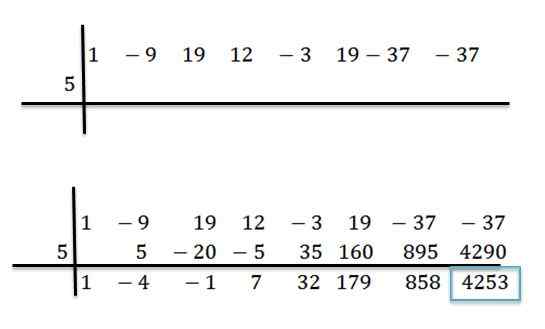

Sebaik sahaja operasi telah dilakukan, kita tahu bahawa kita boleh menulis p (x) seperti berikut:

P (x) = (x⁶-4x⁵ -x⁴+ 7x³ +32x² +179x + 858)*(x-5) + 4253

Oleh itu, semasa menilai, kita perlu:

P (5) = (5-4 (5) -5 +7 (5) +32 (5) +179 (5) +858)*(5-5) +4253

P (5) = (5-4 (5) -5 +7 (5) +32 (5) +179 (5) +858)*(0) +4253

P (5) = 0 + 4253 = 4253

Seperti yang dapat kita lihat, adalah mungkin untuk menggunakan bahagian sintetik untuk mencari nilai polinomial apabila menilai ia dalam c bukan hanya menggantikan c dengan x. 

Sekiranya kita cuba menilai p (5) dengan cara tradisional, kita memerlukan beberapa pengiraan yang biasanya menjadi membosankan.

Contoh 4

Algoritma bahagian untuk polinomial juga dipenuhi untuk polinomial dengan pekali kompleks dan, sebagai akibatnya, kita mempunyai kaedah pembahagian sintetik juga berfungsi untuk polinomial ini. Seterusnya, kita akan melihat contohnya.

Kami akan menggunakan kaedah pembahagian sintetik untuk menunjukkan bahawa z = 1+ 2i adalah sifar polinomial p (x) = x³+ (1+i) x² -(1+2i) x+(15+5i). Iaitu, sisa bahagian p (x) antara d (x) = x - z adalah sama dengan sifar.

Kami meneruskan seperti dahulu: Pada baris pertama kita menulis pekali p (x), kemudian pada kedua kita menulis z dan lukis garis bahagian.

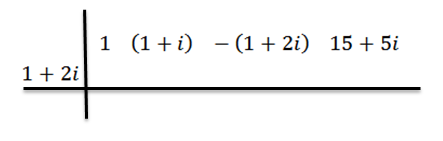
Kami melakukan pembahagian seperti dahulu, itu:

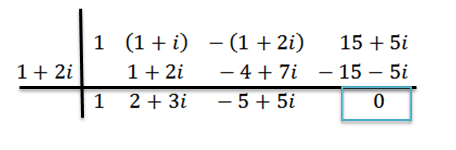
Kita dapat melihat bahawa sisa adalah sifar; Oleh itu, kita menyimpulkan bahawa z = 1+ 2i adalah sifar p (x).

Rujukan

1. Baldor, Aurelio. Algebra. Kumpulan Editorial Patria.
2. Demana, Waits, Foley & Kennedy. Precáculo: grafik, berangka, algebra. Pendidikan Pearson.