Bahagian di mana sisa adalah 300

Terdapat banyak bahagian di mana sisa adalah 300. Di samping memetik sebahagian daripada mereka, teknik akan dipaparkan yang membantu membina setiap bahagian ini, yang tidak bergantung pada nombor 300.

Teknik ini disediakan oleh algoritma bahagian Euclid, yang menetapkan yang berikut: Memandangkan dua bilangan bulat "n" dan "b", dengan "b" berbeza dari sifar (b ≠ 0), terdapat "q" dan "r unik ", seperti n = bq+r, di mana 0 ≤" r " < |b|.

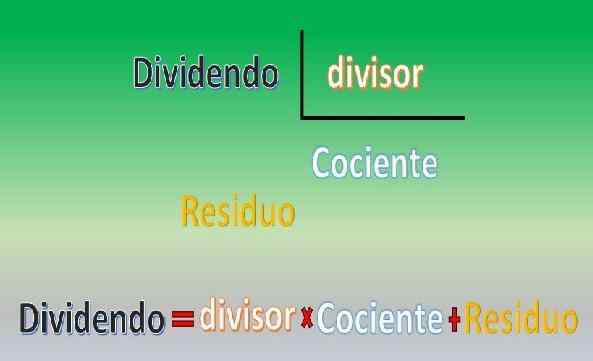
Nombor "n", "b", "q" dan "r" dipanggil dividen, pembahagi, quotient dan residu (atau rehat), masing -masing.

Harus diingat bahawa dengan menuntut bahawa residu menjadi 300, secara tersirat dikatakan bahawa nilai mutlak pembahagi mestilah lebih ketat daripada 300, iaitu: | B |> 300.

Contoh bahagian di mana sisa adalah 300

Berikut adalah beberapa bahagian di mana sisa adalah 300; Kemudian, kaedah pembinaan setiap bahagian dibentangkan.

1- 1000 ÷ 350

Jika 1000 dibahagikan dengan 350, dapat dilihat bahawa kuota adalah 2 dan sisa adalah 300.

2-1500 ÷ 400

Dengan membahagikan 1500 hingga 400, diperolehi bahawa quotient adalah 3 dan sisa adalah 300.

3-3800 ÷ 700

Semasa membuat bahagian ini akan menjadi quotient adalah 5 dan sisa akan menjadi 300.

4- 1350 ÷ (-350)

Apabila bahagian ini diselesaikan, -3 sebagai kuota dan 300 sebagai sisa.

Bagaimana bahagian -bahagian ini dibina?

Untuk membina bahagian sebelumnya, anda hanya perlu menggunakan algoritma bahagian dengan betul.

Empat langkah untuk membina bahagian -bahagian ini adalah:

1- Tetapkan sisa

Seperti yang anda mahukan residu menjadi 300, r = 300 ditetapkan.

2- Pilih pembahagi

Oleh kerana sisa adalah 300, pembahagi yang dipilih mestilah nombor sedemikian rupa sehingga nilai mutlaknya lebih besar daripada 300.

3- Pilih Quotient

Untuk kota, anda boleh memilih bilangan sifar yang berlainan (q ≠ 0).

4- Dividen dikira

Sebaik sahaja sisa, pembahagi dan kuota tetap, mereka digantikan di sebelah kanan algoritma bahagian. Hasilnya akan menjadi bilangan yang mesti dipilih sebagai dividen.

Dengan empat langkah mudah ini, anda dapat melihat bagaimana setiap bahagian senarai dibina. Dalam semua r = 300 ini ditetapkan.

Untuk bahagian pertama, b = 350 dan q = 2 dipilih. Dengan menggantikan algoritma bahagian, 1000 diperolehi sebagai hasilnya. Supaya dividen mestilah 1000.

Untuk bahagian kedua, b = 400 dan q = 3 telah ditubuhkan, sehingga dengan menggantikan algoritma pembahagian, 1500 diperoleh. Oleh itu ditubuhkan bahawa dividen adalah 1500.

Untuk yang ketiga nombor 700 dipilih sebagai pembahagi dan sebagai quotient nombor 5. Apabila menilai nilai -nilai ini dalam algoritma pembahagian, diperolehi bahawa dividen mestilah sama dengan 3800.

Untuk bahagian keempat pembahagi sama dengan -350 dan kuota sama dengan -3. Apabila nilai -nilai ini digantikan dalam algoritma bahagian dan diselesaikan, diperolehi bahawa dividen adalah sama dengan 1350.

Berikutan langkah -langkah ini, banyak lagi bahagian boleh dibina di mana sisa adalah 300, menjaga apabila mereka mahu menggunakan nombor negatif.

Harus diingat bahawa proses pembinaan yang diterangkan di atas boleh digunakan untuk membina bahagian dengan sisa yang berbeza daripada 300. Hanya nombor 300 yang diubah, dalam langkah pertama dan kedua, untuk nombor yang dikehendaki.