120 pembahagi

The 120 pembahagi Mereka semua nombor yang membahagikannya dengan tepat. Nombor ini adalah seperti berikut:

Pembahagi 120 = 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 30, 40, 60, 120

Juga bertentangan dengan nombor ini, iaitu, negatif, adalah 120 pembahagi, kerana pembahagian itu tepat. 120 mempunyai 16 pembahagi keseluruhan positif dan banyak lagi negatif.

Terdapat beberapa cara untuk mencari pembahagi nombor. Sekiranya ini tidak begitu besar, anda boleh menggunakan jadual pendaraban (untuk nombor kurang daripada 100) dan sahkan di mana jadual nombor yang dipersoalkan muncul. Sebagai contoh, 12 muncul dalam jadual 2, 3, 4 dan 6, dan ini adalah pembahagi mereka, bersama -sama dengan 1 dan 12 yang sama.

Nombor itu juga boleh dipecah menjadi faktor utama, menggunakan peraturan pembahagian dan membiak faktor. Tetapi anda harus berhati -hati untuk tidak lulus pembahagi yang diabaikan.

Sebagai 120 lebih besar daripada 100, ia tidak langsung dalam jadual pendaraban, bagaimanapun, tidak terlalu sukar untuk mencari 16. Prosedur yang sah untuk semua nombor ditunjukkan dengan serta -merta, melalui penggunaan jadual yang sangat mudah.

Berapa banyak pembahagi 120?

Pertama, bilangan pembahagi 120 dijumpai. Terdapat formula yang membolehkan anda mengetahui berapa banyak yang anda miliki, walaupun tidak mengatakan apa itu.

Nombor komposit, seperti 120, boleh dinyatakan sebagai produk nombor perdana, atau kuasa ini. Memanggil N ke mana -mana nombor kompaun:

N = aⁿ ∙ b^m ∙ c^p ... r^k

Boleh melayani anda: Hubungan perkadaran: konsep, contoh dan latihan

Nombor A, B, C ... R adalah nombor Perdana, dan nilai N, M, P, ... K, kuasa masing -masing. Penguraian dalam faktor utama 120 adalah seperti berikut:

120 | 2
60 | 2
30 | 2
15 | 3
5 | 5
1 | 1

Dengan cara ini, 120 adalah produk faktor:

120 = 2³ ∙ 3 ∙ 5

Formula untuk mengira bilangan pembahagi n

Bilangan pembahagi = (n +1) × (m +1) × (p +1) ... × (k +1)

Sekarang formula hingga 120 digunakan. Dari penguraian dalam faktor yang anda harus:

n = 3 (adalah kuasa 2)

M = 1 (3 ditinggikan hingga 1: 3¹ = 3)

P = 1 (5 juga muncul tinggi hingga 1)

Dengan nilai -nilai ini:

Bilangan pembahagi 120 = (3 +1) × (1 +1) × (1 +1) = 4 × 2 × 2 = 16

Hasil ini bertepatan dengan permulaan permulaan: 120 mempunyai 16 pembahagi. Di samping itu, sudah diketahui bahawa 2, 3 dan 5 adalah pembahagi 120, serta 10, kerana mana -mana nombor selesai dalam 0 boleh dibahagikan dengan 10. Prosedur untuk mencari mereka semua ditunjukkan dengan segera.

Pengiraan pembahagi 120

Ia dilakukan dengan bantuan faktor -faktor yang dikira di bahagian sebelumnya. Di sana dilihat bahawa 2 adalah faktor utama dengan eksponen 3, dan 3 adalah faktor sepupu yang lain, dengan eksponen 1. Dengan maklumat ini jadual berikut dibina:

Perhatikan bahawa kuasa 2 bermula dalam 2⁰ dan berakhir di 2³, yang merupakan faktor yang timbul ketika menguraikan 120. Ingat bahawa 2⁰ dan 3⁰ Kedua -duanya sama dengan 1 (mana -mana nombor tinggi hingga 0 adalah 1). Untuk Faktor 3, ia bermula dalam 3⁰ Sehingga 3¹, Sejak 3¹ = 3.

Seterusnya, jadual selesai dengan produk nombor merah, seperti yang ditunjukkan di sini:

Boleh melayani anda: songsang berbilang: penjelasan, contoh, latihan yang diselesaikan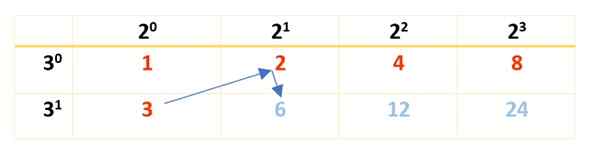

Semua nombor merah dan biru adalah 120 pembahagi, tetapi hampir 8. Untuk mencari yang tersisa, meja baru pecah, pembahagi yang telah diperoleh di barisan depan dan faktor yang masih perlu diambil kira ditulis: 5, dengan kuasa mereka di lajur pertama, ke kiri, seperti ini:

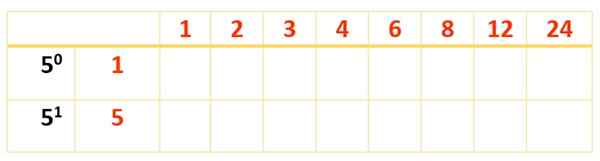
Sekarang, jadual selesai dengan produk nombor merah, seperti yang dilakukan dengan jadual pertama:

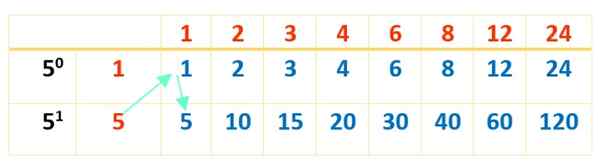
Dan akhirnya 16 pembahagi 120 dalam warna biru muncul. Jadual -jadual ini merupakan bantuan yang sangat baik untuk operasi dilakukan dengan teratur dan oleh itu tidak ada 120 pembahagi.

Latihan yang diselesaikan

Prosedur untuk mencari semua pembahagi nombor diringkaskan seperti berikut:

1. Pecahkan nombor menjadi faktor utama.
2. Kirakan bilangan pembahagi dengan formula.
3. Bina jadual yang diperlukan untuk mencari pembahagi. Jika nombor mempunyai dua faktor, jadual sudah cukup, jika anda mempunyai tiga faktor, dua jadual mesti dibuat, seperti dalam kes 120.

Latihan 1

Cari semua pembahagi 288.

Penyelesaian

288 terurai menjadi faktor utama:

288 | 2
144 | 2
72 | 2
36 | 2
18 | 2
9 | 3
3 | 3
1 | 1

288 ditulis seperti ini:

288 = 2⁵ ∙ 3²

Segera adalah bilangan pembahagi 288 melalui:

Bilangan pembahagi = (n +1) × (m +1) × (p +1) ... × (k +1)

Dari penguraian dalam faktor utama, dinyatakan bahawa n = 5 dan m = 2, maka:

Pembahagi 288 = (5 +1) × (2 +1) = 6 × 3 = 18

Terdapat 18 pembahagi dan kerana terdapat hanya dua faktor, ia cukup dengan hanya satu jadual:

Dapat melayani anda: ciri segi empat tepat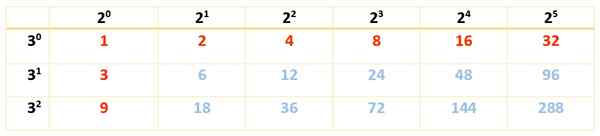

Pembahagi 288 adalah nombor merah dan biru:

Div (288) = 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 72, 96, 144, 288

Mereka boleh diperiksa dengan cepat dengan bantuan kalkulator.

Latihan 2

Cari pembahagi 350

Penyelesaian

350 terurai:

350 | 2
175 | 5
35 | 5
7 | 7
1 | 1

350 boleh ditulis sebagai produk dari tiga faktor:

350 = 2 ∙ 5²∙ 7

Langkah seterusnya adalah untuk mengira berapa banyak pembahagi, melalui formula:

Bilangan pembahagi = (n +1) × (m +1) × (p +1) ... × (k +1)

Dengan n = 1, m = 2, p = 1

Pembahagi 288 = (1 +1) × (2 +1) × (1 +1) = 2 × 3 × 2 = 12

Memandangkan 350 memerlukan tiga faktor, dua jadual mesti dibuat. Yang pertama dilakukan dengan 2 dan 5², Tetapi ia juga boleh dilakukan dengan 2 dan 7, atau dengan 7 dan 5², Mengikut keutamaan, kerana dalam semua bentuk, hasil akhir adalah sama:

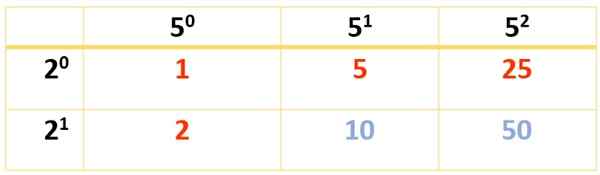
6 pembahagi diperoleh. Yang lain muncul dengan bantuan jadual lain ini:

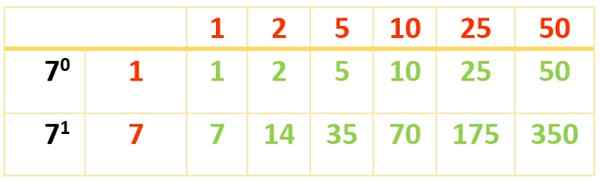
Pembahagi 350 adalah:

Div (350) = 1, 2, 5, 7, 10, 14, 25, 35, 50, 70, 175, 350