Persamaan kesinambungan

Kami menerangkan apakah persamaan kesinambungan, formula, aplikasi, contoh dan mencadangkan latihan untuk menyelesaikannya

Apakah persamaan kesinambungan?

The persamaan kesinambungan, Untuk cecair yang tidak dapat dikompresikan, ia menetapkan bahawa jumlah jisim cecair yang beredar melalui tiub, tanpa kehilangan atau keuntungan, tetap malar. Dengan kata lain, doh dipelihara tanpa perubahan apabila cecair bergerak.

Cecair yang tidak dapat dikompresikan ialah ketumpatannya kekal kira -kira tetap semasa mengalir. Sebagai contoh, air adalah cecair yang dianggap tidak dapat dikompresikan di bawah tekanan standard dan keadaan suhu.

Terdapat cara matematik untuk menyatakan pemuliharaan jisim, dalam persamaan kesinambungan, yang diberikan oleh:

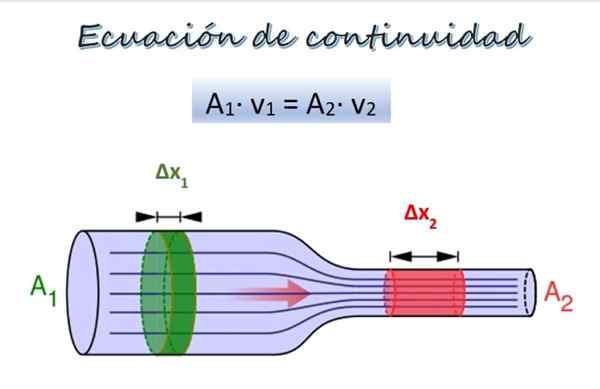
Ke₁∙ v₁ = A₂∙ v₂

Di mana v₁ dan v₂ Mereka mewakili kelajuan cecair dalam dua bahagian paip, sementara₁ sudah₂ Mereka adalah kawasan keratan rentas masing -masing.

Produk kawasan keratan rentas dengan kelajuan dipanggil aliran Dan persamaan kesinambungan menunjukkan bahawa, sepanjang paip, alirannya tetap. Aliran juga dikenali sebagai kadar aliran volum, Difahamkan dengan berhati -hati memerhatikan ungkapan sebelumnya, dimensinya adalah isipadu per unit waktu.

Formula

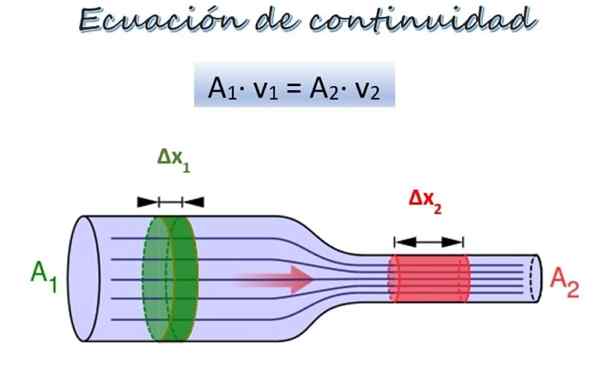Persamaan kesinambungan untuk aliran cecair di sepanjang paip diameter yang berbeza. Sumber: Wikimedia Commons/F. Zapata.

Di bahagian atas terdapat paip dengan dua bahagian diameter yang berbeza dan pada ketinggian yang sama, walaupun mereka boleh berada di ketinggian yang berbeza tanpa mewakili masalah.

Dalam Bahagian 1, lebih luas, kawasan keratan rentas adalah untuk₁ dan bendalir bergerak dengan kelajuan v₁, Semasa berada di Bahagian 2, sempit, kawasan silang silang adalah untuk₂ dan kelajuan bendalir adalah v₂.

Bahagian doh Δm₁ (hijau) bergerak mengikut bahagian 1 dalam satu masa Δt. Dalam tempoh ini, bahagian Δm₂ (Merah) Melalui Bahagian 2. Oleh kerana cecair tidak dapat dikompresikan, ketumpatannya adalah sama dalam semua titiknya, jadi bermula dari definisi ketumpatan:

Ia boleh melayani anda: pemalar gas: apakah, pengiraan dan contoh

Di sini ρ adalah ketumpatan, m adalah jisim jisim dan v. Menurut ini, jisim Δm₁ adalah sama dengan:

Δm₁ = ρ ∙ v₁

Di mana volum v₁ Ia adalah produk antara bahagian silang dan jarak Δx₁:

Δm₁ = ρ ∙ (a₁ ∙ Δx₁)

Tetapi sejak:

Kemudian bahagian doh Δm₁ Anda boleh menulis, dari segi kelajuan dan masa Δt sebagai:

Δm₁ = ρ ∙ a₁ ∙ Δx₁ = ρ ∙ a₁ ∙ (v₁ ∙ Δt)

Analog bahagian Δm ditulis₂ yang mengalir pada masa yang sama oleh Bahagian 2:

Δm₂ = ρ ∙ a₂ ∙ Δx₂ = ρ ∙ a₂ ∙ (v₂ ∙ Δt)

Dengan pemuliharaan jisim:

Δm₁ = Δm₂

Dan:

ρ ∙ a₁ ∙ v₁ ∙ Δt = ρ ∙ a₂ ∙ v₂ ∙ Δt

Oleh kerana Δt dan ρ dibatalkan, hasilnya:

Ke₁ ∙ v₁ = A₂ ∙ v₂

Aliran q

Produk bahagian silang A dengan kelajuan bendalir v dipanggil aliran dan menandakan sebagai q. Ia bersamaan dengan jumlah cecair per unit masa melalui paip, atau kadar aliran kelantangan:

 Volum v dan ΔT selang masa. Kadar aliran dalam sistem unit antarabangsa adalah m³/s, walaupun kaki padu, gelen/min, gelen/s liter/s dan gelen/s adalah kerap. Beberapa faktor penukaran yang paling banyak digunakan adalah seperti berikut:

• 1 m³/S = 264.172 gal/s
• 1 l/s = 0.001 m³/s
• 1 kaki³/S = 0.0283168 m³/s
• 1 l/s = 0.264172 gal/s
• 1 m³/S = 15850.3 gal/min

Perhatikan bahawa, dengan mengurangkan bahagian silang tiub, kelajuan bendalir meningkat, dan sebaliknya, jika bahagian silang meningkat, maka kelajuan berkurangan sehingga alirannya tetap.

Aplikasi dan contoh

Persamaan kesinambungan digunakan dalam analisis aliran bendalir, digabungkan dengan persamaan Bernoulli, di mana variasi kelajuan bendalir di bahagian yang berbeza diambil kira, serta perubahan tekanan dan kesan ketinggian.

Boleh melayani anda: Arus langsung

Contoh 1

Di dalam hos kebun keluarga, apabila air biasanya meninggalkan jet mempunyai julat tertentu, tetapi jika ia meletakkan jarinya di pintu keluar hos, mengurangkan lubang output, julat jet lebih besar adalah.

Di sini persamaan kesinambungan dipenuhi, kerana, dengan mengurangkan kawasan muncung output, kelajuan jet meningkat sehingga kawasan kelajuan dengan kelajuan tetap.

Contoh 2

Jet air sempit ketika jatuh, kerana kelajuannya meningkat. Dengan cara ini kelajuan produk setiap kawasan tetap berterusan

Satu lagi contoh di mana persamaan kesinambungan diketengahkan ialah jet air yang menyempit ketika jatuh, disebabkan peningkatan kelajuan air semasa musim gugur.

Dengan cara ini alirannya tetap, sementara jet terus mengalir dalam rejim laminar, iaitu air jatuh perlahan -lahan tanpa pergolakan atau pusaran.

Latihan yang diselesaikan

Latihan 1

Air beredar melalui paip diameter 20 cm. Mengetahui bahawa alirannya adalah 2000 l/s, cari kelajuan air di paip.

• Penyelesaian

Adalah mudah untuk menyatakan segala -galanya dalam unit sistem antarabangsa. Pertama, seksyen keratan rentas paip dikira, ingat bahawa radius adalah separuh diameter:

A = π ∙ (D/2)²

D = 20 cm = 0.2 m

Oleh itu, kawasan itu adalah:

A = π ∙ (D/2)² = A = π ∙ (0.2 m /2)² = 0.0314 m².

Aliran dinyatakan dalam m³/s dengan bantuan faktor penukaran yang sesuai:

Q = 2000 l/s = 2 m³/s

Dari formula q = a ∙ v kelajuan yang bendalir beredar melalui paip dibersihkan:

Latihan 2

Anda mempunyai paip -paip yang berubah -ubah di mana air mengalir. Pada titik tertentu, bahagian silang adalah 0.070 m² Dan kelajuan air adalah 3.50 m/s. Kira:

Boleh melayani anda: Prinsip Pascal: Sejarah, Aplikasi, Contoh

a) Kelajuan air di titik lain di paip yang kawasan silangnya adalah 0.105 m².

b) Jumlah air yang dilepaskan dengan ujung terbuka dalam 1 jam.

• Penyelesaian kepada

Persamaan kesinambungan digunakan, sepadan dengan aliran titik pertama dengan aliran kedua. Alirannya:

Q = A ∙ V

Untuk kesinambungan:

Q₁ = Q₂

Ke₁ ∙ v₁ = A₂ ∙ v₂

Sekarang mereka menggantikan data yang disediakan oleh pernyataan:

• Ke₁ = 0.070 m²
• v₁ = 3.50 m/s
• Ke₂ = 0.105 m²
• v₂ =?

Dan membersihkan v₂:

Penyelesaian b

Oleh kerana aliran juga jumlah per unit masa, ia harus:

Oleh itu, Volume V adalah:

V = q ∙ Δt = (a ∙ v) Δt

Aliran yang boleh dikira dengan data titik 1 atau yang titik 2, kerana ia sama pada kedua -dua titik:

Q = a₁ ∙ v₁ = 0.070 m² ∙ 3.50 m/s = 0.245 m³ / s

Mengetahui bahawa 1 jam = 3600 s, jumlah air yang dilepaskan adalah:

V = q ∙ Δt = (0.245 m³ / s) × (3600 s) = 882 m³

Dalam 1 jam 882 m dimuat turun³ air melalui paip.