Formula Persamaan Ijazah Kedua, Cara Menyelesaikannya, Contoh, Latihan
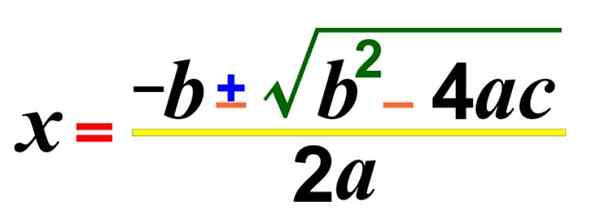
- 1104
- 214
- Miss Elmer Hagenes
The Persamaan ijazah kedua atau kuadrat Dan yang tidak diketahui mempunyai borang kapak2 + bx + c = 0. Di mana ≠ 0, kerana menjadi 0, persamaan akan diubah menjadi persamaan linear, dan pekali a, b dan c adalah nombor sebenar.
Yang tidak diketahui ditentukan adalah nilai x. Contohnya, persamaan 3x2 - 5x + 2 = 0 adalah persamaan darjah kedua yang lengkap.
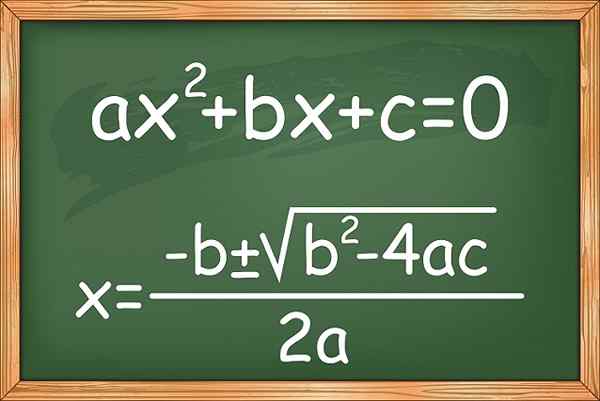 Rajah 1. Formula untuk menyelesaikan ijazah kedua atau persamaan kuadratik yang tidak diketahui
Rajah 1. Formula untuk menyelesaikan ijazah kedua atau persamaan kuadratik yang tidak diketahui Terdapat juga variasi yang dikenali sebagai persamaan kedua yang tidak lengkap, yang tidak mempunyai sebarang terma, kecuali kapak2. Berikut adalah beberapa contoh:
x2 - 25 = 0
3x2 - 5x = 0
Al Juarismi, ahli matematik Arab yang terkenal, yang diterangkan dalam karya -karyanya pelbagai jenis persamaan darjah pertama dan kedua, tetapi hanya dengan pekali positif. Walau bagaimanapun, ia adalah matematik Perancis Menyelesaikan:
Ini adalah formula umum yang membolehkan menyelesaikan persamaan kuadrat, mencari akar atau sifar yang sama, walaupun penyelesaiannya tidak nyata. Terdapat juga cara lain untuk menyelesaikannya.
[TOC]
Cara menyelesaikan persamaan gred kedua?
Persamaan kedua -dua dapat diselesaikan dengan formula yang diberikan di atas, dan terdapat juga prosedur algebra lain yang dapat berfungsi dalam beberapa persamaan.
Kami akan menyelesaikan persamaan yang dicadangkan pada mulanya dengan formula, kaedah yang sah untuk mana -mana persamaan darjah kedua dengan yang tidak diketahui:
3x2 - 5x + 2 = 0
Untuk menggunakan formula yang kita perhatikan dengan betul:
- ke Ia adalah pekali istilah dengan x2
- b Ia adalah pekali istilah linear
- c adalah istilah bebas.
Mari kita kenal pasti mereka dari persamaan yang sama:
A = 3
B = -5
C = 2
Perhatikan bahawa tanda yang mengiringi pekali mesti diambil kira. Sekarang kita menggantikan nilai -nilai ini dalam formula:
Dalam pengangka adalah simbol "lebih - kurang" ±, yang menunjukkan bahawa kuantiti dengan akar boleh diambil sebagai positif dan juga sebagai negatif. Persamaan ijazah kedua mempunyai maksimum dua penyelesaian sebenar, dan simbol ini mengambil kira.
Mari panggil x1 dan x2 Kepada kedua -dua penyelesaian ini, maka:
x1 = (5+1) / 6 = 1
x2 = (5-1)/6 = 4/6 = 2/3
Resolusi dengan pemfaktoran
Beberapa persamaan darjah kedua terdiri daripada trinomial yang mudah faktor. Jika ya, kaedah ini jauh lebih cepat. Pertimbangkan persamaan:
x2 + 7x - 18 = 0
Faktorisasi mempunyai bentuk ini:
Boleh melayani anda: Congruence: angka kongruen, kriteria, contoh, latihan(x +) ⋅ (x -)
Ruang kosong dipenuhi dengan dua nombor yang, apabila didarabkan pada 18, dan apabila mereka ditolak, 7 adalah 7. Tanda -tanda dalam kurungan dipilih dengan kriteria ini:
-Dalam kurungan pertama, tanda antara istilah pertama dan kedua diletakkan.
-Dan dalam kurungan kedua menghasilkan produk tanda -tanda yang dilihat.
Bagi nombor, mereka mudah dalam kes ini: mereka adalah 9 dan 2. Yang paling sulung sentiasa diletakkan di dalam kurungan pertama, seperti ini:
x2 + 7x - 18 = (x + 9). (x - 2)
Pembaca boleh menyemak melalui harta pengedaran, yang apabila membangunkan produk di sebelah kanan persamaan, trinomial kiri diperolehi. Sekarang, persamaan ditulis semula:
(x + 9) ⋅ (x - 2) = 0
Untuk kesamaan yang perlu dipenuhi, sudah cukup untuk salah satu daripada dua faktor yang menjadi sifar. Jadi, pada yang pertama ia mesti dilakukan1 = -9 atau mungkin faktor kedua dibatalkan, dalam hal ini x2 = 2. Ini adalah penyelesaian persamaan.
Kaedah grafik
Akar atau penyelesaian persamaan darjah kedua sesuai dengan persimpangan perumpamaan y = = kapak2 + bx + c Dengan paksi mendatar atau paksi x. Sehingga dengan grafik perumpamaan yang sepadan kita akan mencari penyelesaian persamaan darjah kedua yang dilakukan y = 0.
Potongan perumpamaan dengan paksi mendatar mewakili penyelesaian persamaan kapak2 + bx + c = 0. Perumpamaan yang hanya memotong paksi mendatar pada satu titik mempunyai akar tunggal dan ini akan selalu menjadi puncak parabola.
Dan akhirnya, jika perumpamaan tidak dipotong ke paksi mendatar, persamaan yang sepadan kapak2 + bx + c = 0 Ia tidak mempunyai penyelesaian yang nyata.
Membina graf tangan boleh menjadi susah payah, tetapi dengan menggunakan program yang graf dalam talian sangat mudah.
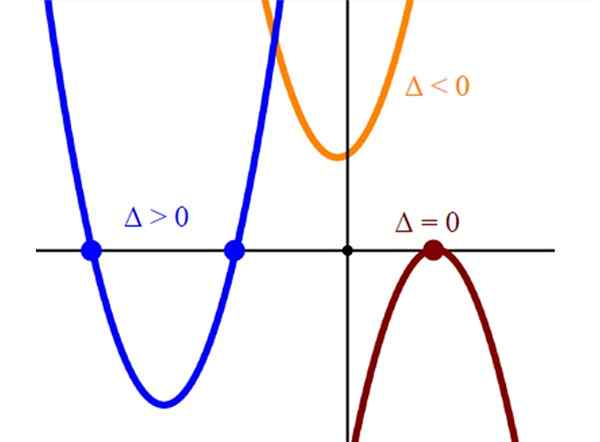 Rajah 2. Perwakilan grafik tiga jenis perumpamaan, dengan dua, satu dan tiada persimpangan dengan paksi mendatar. Sumber: Wikimedia Commons.
Rajah 2. Perwakilan grafik tiga jenis perumpamaan, dengan dua, satu dan tiada persimpangan dengan paksi mendatar. Sumber: Wikimedia Commons. Resolusi dengan kalkulator saintifik
Banyak model kalkulator saintifik mempunyai pilihan untuk menyelesaikan persamaan darjah kedua (dan juga jenis persamaan lain). Untuk mengetahui, anda perlu menyemak menu.
Setelah pilihan persamaan kuadratik yang tidak diketahui dipilih, permintaan menu untuk memasukkan nilai pekali a, b dan c dan mengembalikan penyelesaian sebenar jika mereka wujud. Dan terdapat juga model kalkulator saintifik yang bekerja dengan nombor yang kompleks dan menawarkan penyelesaian ini.
Boleh melayani anda: gandaan 2: apa dan penjelasanMembezakan dari persamaan darjah kedua
Untuk mengetahui sama ada persamaan mempunyai penyelesaian sebenar atau tidak, dan berapa banyak, tanpa perlu menyelesaikannya terlebih dahulu, diskriminasi ditakrifkan sebagai amaun di bawah akar kuadrat:
Δ = b2 - 4ac
Menurut tanda diskriminasi, diketahui berapa banyak penyelesaian persamaan yang sesuai dengan kriteria ini:
-Dua penyelesaian sebenar: δ> 0
-Penyelesaian sebenar (atau dua penyelesaian yang sama): δ = 0
-Tiada penyelesaian sebenar: δ < 0
Contohnya, berapa banyak penyelesaian yang dilakukan oleh persamaan darjah kedua -7x2 +12x + 64 = 0? Kami mengenal pasti pekali:
A = -7
B = 12
C = 64
Δ = b2 - 4ac = 122 - 4x (-7) x 64 = 144 + 1792 = 1936> 0
Persamaan mempunyai dua penyelesaian. Sekarang mari kita lihat yang ini:
x2 - 6x + 9 = 0
A = 1
B = -6
C = 9
Δ = (-6)2 - 4 x 1 x 9 = 36 - 36 = 0
Ini adalah persamaan dengan penyelesaian unik atau dua penyelesaian yang sama.
Contoh Persamaan Ijazah Kedua Mudah
Pada mulanya kita mengatakan bahawa persamaan darjah kedua dapat selesai jika trinomial adalah, dan tidak lengkap jika istilah linear atau istilah bebas hilang. Sekarang mari kita lihat beberapa jenis tertentu:
Persamaan borang x2 + mx + n = 0
Dalam kes ini A = 1 dan formula dikurangkan kepada:
Untuk persamaan jenis ini, dan sentiasa bergantung pada pekali yang selebihnya, kaedah pemfaktoran dapat berfungsi dengan baik, seperti yang kita lihat di bahagian sebelumnya.
Persamaan bentuk kapak yang tidak lengkap2 + C = 0
Penyelesaiannya, jika ada, adalah bentuk:
Terdapat penyelesaian sebenar apabila O C mempunyai tanda negatif, tetapi jika kedua -dua istilah mempunyai tanda yang sama, penyelesaiannya akan menjadi khayalan.
Persamaan bentuk kapak yang tidak lengkap2 + Bx = 0
Persamaan ini dengan cepat diselesaikan dengan menggunakan pemfaktoran, kerana x adalah faktor biasa dalam kedua -dua istilah. Salah satu penyelesaiannya selalu x = 0, yang lain seperti ini:
kapak2 + Bx = 0
x (kapak + b) = 0
kapak + b = 0 → x = -b/a
Mari lihat contohnya. Menyelesaikan:
x2 - 5x = 0
x (x - 5) = 0
Oleh itu x1 = 0 dan x2 = 5
Persamaan dengan penyebut
Terdapat beberapa persamaan rasional, di mana yang tidak diketahui dapat hadir dalam pengangka dan dalam penyebut, atau bahkan hanya di dalamnya, dan oleh manipulasi algebra dikurangkan kepada persamaan kuadrat.
Cara untuk menyelesaikannya adalah untuk membiak kedua -dua belah persamaan dengan pelbagai minimum atau m.c.m dari penyebut dan kemudian menyusun semula istilah. Sebagai contoh:
Boleh melayani anda: Berapa banyak diameter yang mempunyai lilitan?Persamaan pesanan yang lebih tinggi yang diubah menjadi kuadrat
Terdapat persamaan pesanan yang lebih tinggi yang, melalui perubahan berubah, dapat diselesaikan seolah -olah mereka kuadrat, contohnya persamaan ini Bicadrada:
x4 - 10x2 + 9 = 0
Biarkan x2 = U, maka persamaannya berubah menjadi:
atau2 - 10U + 9 = 0
Persamaan ini dengan cepat diselesaikan dengan pemfaktoran, mencari dua nombor yang didarabkan dalam 9 dan menambah 10. Nombor ini 9 dan 1:
(U - 9).(U - 1) = 0
Oleh itu penyelesaian persamaan ini adalah u1 = 9 dan u2 = 1. Sekarang kita mengembalikan perubahan:
x2 = 9 → x1 = 3 dan x2 = -3
x2 = 1 → x1 = 1 dan x2 = -1
Persamaan asal adalah perintah 4, oleh itu ia mempunyai sekurang -kurangnya 4 akar. Contohnya ialah -3, -1, 1 dan 3.
Latihan mudah diselesaikan
- Latihan 1
Selesaikan persamaan kuadrat berikut dengan yang tidak diketahui dalam penyebut:
Pelbagai biasa minimum adalah x (x+2) dan mesti membiak untuk semua istilah:
Ekspresi bersamaan tetap:
5x (x+2) - x = x (x+2)
Kami membangunkan:
5x2 + 10x - x = x2 + 2x
Semua istilah dipindahkan ke kiri kesamaan dan ke kanan dibiarkan 0:
5x2 + 10x - x - x2 - 2x = 0
4x2 - 7x = 0
Kami faktor, kerana ia adalah persamaan yang tidak lengkap:
x (4x - 7) = 0
Salah satu penyelesaiannya ialah x = 0, yang lain adalah:
4x = 7
x = 7/4
- Latihan 2
Cari penyelesaian persamaan darjah kedua:
a) -7x2 +12x + 64 = 0
b) x2 - 6x + 9 = 0
Penyelesaian kepada
Dari persamaan ini kita tahu penentu δ, kerana ia dikira sebagai contoh sebelum ini, jadi kita akan memanfaatkannya, menyatakan formula pelarut seperti berikut:
x1 = (-12+44)/ - 14 = - (32/14) = - (16/7)
x2 = (-12 -44) / -14 = 4
Penyelesaian b
Trinomial persegi x2 - 6x + 9 boleh difikirkan, kerana ia adalah trinomial persegi yang sempurna:
x2 - 6x + 9 = (x-3)2 = 0
Penyelesaian persamaan ini ialah x = 3.
- Latihan 3
Apakah persamaan yang penyelesaiannya adalah 3 dan 4?
Penyelesaian
Ekspresi yang difokuskan ialah:
(x - 3) ⋅ (x - 4) = 0
Memohon harta pengedaran:
x2 - 4x -3x + 12 = 0
Kedua -dua istilah utama adalah serupa dan dapat dikurangkan, menjadi: meninggalkan:
x2 - 7x + 12 = 0
Rujukan
- Baldor. 1977. Algebra Elementary. Edisi Kebudayaan Venezuela.
- Hoffman, J. Pemilihan masalah matematik. Jilid 2.
- Jiménez, r. 2008. Algebra. Prentice Hall.
- Stewart, J. 2006. Preccculment: Matematik untuk Pengiraan. 5th. Edisi. Pembelajaran Cengage.
- Zapata, f. 4 cara untuk menyelesaikan persamaan darjah kedua. Pulih dari: Francesphysics.Blogspot.com.
- Zill, d. 1984. Algebra dan trigonometri. McGraw Hill.



\pm&space;\sqrt(-5)^2-4\times&space;3\times&space;22\times&space;3=)

^2-4c2)


x-\fracx(x+2)x+2=x(x+2))
=\frac-12\pm&space;44-14)