Persamaan Polinom

Apakah persamaan polinomial?

The Persamaan Polinom Mereka adalah pernyataan yang menimbulkan kesamaan dua ungkapan atau ahli, di mana sekurang -kurangnya salah satu istilah yang membentuk setiap sisi kesamaan adalah polinomial p (x). Persamaan ini dinamakan mengikut tahap pembolehubah mereka.

Secara umum, persamaan adalah pernyataan yang menetapkan kesamaan dua ungkapan, di mana sekurang -kurangnya satu dari ini terdapat jumlah yang tidak diketahui, yang dipanggil pembolehubah atau tidak diketahui. Walaupun terdapat banyak jenis persamaan, ini biasanya diklasifikasikan kepada dua jenis: algebra dan transenden.

Persamaan polinom hanya mengandungi ungkapan algebra, yang boleh mempunyai satu atau lebih yang tidak diketahui yang campur tangan dalam persamaan. Menurut eksponen (gred) yang mereka ada, mereka boleh diklasifikasikan sebagai: gred pertama (linear), gred kedua (kuadratik), gred ketiga (padu), gred keempat (quantic), darjah lebih besar daripada atau sama dengan lima dan tidak rasional.

Ciri -ciri persamaan polinomial

Persamaan polinom adalah ungkapan yang dibentuk oleh kesamaan antara dua polinomial; Iaitu, untuk jumlah pendaraban yang terhingga antara nilai yang tidak diketahui (pembolehubah) dan nombor tetap (pekali), di mana pembolehubah boleh mempunyai eksponen, dan nilai mereka boleh menjadi integer positif, termasuk sifar.

Eksponen menentukan tahap atau jenis persamaan. Istilah ungkapan yang mempunyai eksponen paling nilai akan mewakili tahap polinomial mutlak.

Persamaan polinom juga dikenali sebagai algebra, pekali mereka boleh menjadi nombor sebenar atau kompleks dan pembolehubah adalah nombor yang tidak diketahui yang diwakili oleh huruf, seperti: "x".

Jika dengan menggantikan nilai dengan pemboleh ubah "x" dalam p (x) hasilnya sama dengan sifar (0), maka dikatakan bahawa nilai ini memenuhi persamaan (ia adalah penyelesaian), dan umumnya dipanggil akar polinomial.

Apabila persamaan polinomial dibangunkan, semua akar atau penyelesaian mahu dijumpai.

Jenis persamaan polinomial

Terdapat beberapa jenis persamaan polinomial, yang dibezakan mengikut bilangan pembolehubah, dan juga mengikut tahap eksponen mereka.

Oleh itu, persamaan polinomial -di mana istilah pertamanya adalah polinomial yang hanya tidak diketahui, memandangkan ijazahnya boleh menjadi nombor semulajadi (n) dan istilah kedua adalah sifar -boleh dinyatakan seperti berikut:

Boleh melayani anda: Sejarah Trigonometri dari Asalnya

ke_{N *} xⁿ + ke_{N-1 *} x^N-1 +... + a_{1 *} x¹ + ke_{0 *} x₀ = 0

Di mana:

• ke_n, ke_N-1 sudah₀, Mereka adalah pekali sebenar (nombor).
• ke_n berbeza dengan sifar.
• Exponent N adalah integer positif yang mewakili tahap persamaan.
• x adalah pemboleh ubah atau tidak diketahui yang mesti dicari.

Tahap mutlak atau lebih besar persamaan polinomial adalah bahawa eksponen nilai yang lebih besar di antara semua yang membentuk polinomial; Dengan cara ini, persamaan diklasifikasikan sebagai:

Gred pertama

Persamaan polinomial tahap pertama, yang juga dikenali sebagai persamaan linear, adalah yang mana ijazah (eksponen terbesar) adalah sama dengan 1, polinomial adalah bentuk p (x) = 0; Dan ia terdiri daripada linear dan istilah bebas. Ia ditulis seperti berikut:

kapak + b = 0.

Di mana:

• A dan B adalah nombor sebenar dan ≠ 0.
• Kapak adalah istilah linear.
• B adalah istilah bebas.

Contohnya, Persamaan 13x - 18 = 4x.

Untuk menyelesaikan persamaan linear, semua istilah yang mengandungi x yang tidak diketahui mesti diluluskan ke sisi kesamaan, dan mereka yang tidak bergerak di sisi lain, untuk membersihkannya dan mendapatkan penyelesaian:

13x - 18 = 4x

13x = 4x + 18

13x - 4x = 18

9x = 18

x = 18 ÷ 9

x = 2.

Dengan cara ini, persamaan yang diberikan hanya mempunyai satu penyelesaian atau akar, iaitu x = 2.

Gred kedua

Persamaan polinomial darjah kedua, yang juga dikenali sebagai persamaan kuadrat, adalah di mana ijazah (eksponen terbesar) adalah sama dengan 2, polinomial adalah bentuk p (x) = 0, dan terdiri daripada istilah kuadratik, a linear dan bebas. Ia dinyatakan seperti berikut:

kapak² + bx + c = 0.

Di mana:

• A, B dan C adalah nombor sebenar dan ≠ 0.
• kapak² Ia adalah istilah kuadratik, dan "a" adalah pekali istilah kuadrat.
• Bx adalah istilah linear, dan "b" adalah pekali istilah linear.
• C adalah istilah bebas.

Menyelesaikan

Umumnya, penyelesaian kepada persamaan jenis ini diberikan apabila membersihkan x persamaan, dan kekal seperti berikut, yang dipanggil resolven:

Boleh melayani anda: Teorem Binomial

Di sana, (b² - 4ac) dipanggil membezakan dari persamaan dan ungkapan ini menentukan bilangan penyelesaian yang dapat dimiliki oleh persamaan:

• Ya (b² - 4ac) = 0, persamaan akan mempunyai satu penyelesaian yang berganda; iaitu, ia akan mempunyai dua penyelesaian yang sama.
• Ya (b² - 4ac)> 0, persamaan akan mempunyai dua penyelesaian sebenar yang berbeza.
• Ya (b² - 4ac) < 0, la ecuación no tiene solución (tendrá dos soluciones complejas distintas).

Contohnya, anda mempunyai persamaan 4x² + 10x - 6 = 0, untuk menyelesaikannya terlebih dahulu istilah A, B dan C dikenalpasti, dan kemudian ia digantikan dalam formula:

A = 4

B = 10

C = -6.

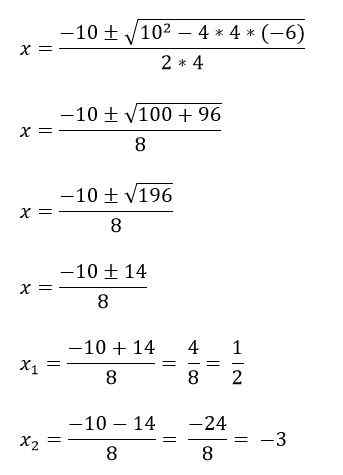
Terdapat kes -kes di mana persamaan polinomial kedua -dua tidak mempunyai tiga istilah, dan itulah sebabnya mereka diselesaikan secara berbeza:

• Sekiranya persamaan kuadratik tidak mempunyai istilah linear (iaitu, b = 0), persamaan akan dinyatakan sebagai kapak² + C = 0. Untuk menyelesaikannya, x dibersihkan² Dan akar persegi digunakan dalam setiap ahli, mengingati bahawa dua tanda yang mungkin tidak diketahui:

kapak² + C = 0.

x² = - c ÷ a

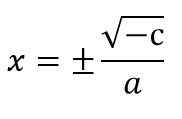
Contohnya, 5 x² - 20 = 0.

5 x² = 20

x² = 20 ÷ 5

x = ± √4

x = ± 2

x₁ = 2.

x₂ = -2.

• Apabila persamaan kuadratik tidak mempunyai istilah bebas (iaitu, c = 0), persamaan akan dinyatakan sebagai kapak² + Bx = 0. Untuk menyelesaikannya, faktor umum X yang tidak diketahui mesti diambil pada ahli pertama; Oleh kerana persamaan dipadankan dengan sifar, ia dipenuhi bahawa sekurang -kurangnya salah satu faktor akan sama dengan 0:

kapak² + Bx = 0.

x (kapak + b) = 0.

Dengan cara ini, anda mesti:

x = 0.

x = -b ÷ a.

Contohnya: anda mempunyai persamaan 5x² + 30x = 0. Pertama ia menjadi faktor:

5x² + 30x = 0

x (5x + 30) = 0.

Dua faktor dijana iaitu x y (5x + 30). Salah satu daripada ini akan dianggap sebagai sifar dan yang lain diberi penyelesaian:

x₁ = 0.

5x + 30 = 0

5x = -30

x = -30 ÷ 5

x₂ = -6.

Gred tertinggi

Persamaan polinomial darjah utama adalah yang terdiri daripada gred ketiga dan seterusnya, yang boleh dinyatakan atau diselesaikan dengan persamaan polinomial umum untuk sebarang tahap:

Boleh melayani anda: pekali korelasi: formula, pengiraan, tafsiran, contoh

ke_{N *} xⁿ + ke_{N-1 *} x^N-1 +... + a_{1 *} x¹ + ke_{0 *} x₀ = 0

Ini digunakan kerana persamaan dengan tahap yang lebih besar daripada dua adalah hasil dari pemfaktoran polinomial; iaitu, ia dinyatakan sebagai pendaraban polinomial gred satu atau lebih besar, tetapi tanpa akar sebenar.

Penyelesaian persamaan jenis ini adalah langsung, kerana pendaraban dua faktor akan sama dengan sifar jika mana -mana faktor adalah batal (0); Oleh itu, setiap persamaan polinomial yang dijumpai mesti diselesaikan, sepadan dengan setiap faktornya kepada sifar.

Sebagai contoh, anda mempunyai persamaan darjah ketiga (padu) x³ + x² +4x + 4 = 0. Untuk menyelesaikannya, anda harus mengikuti langkah -langkah berikut:

• Terma dikumpulkan:

x³ + x² +4x + 4 = 0

(x³ + x² ) + (4x + 4) = 0.

• Ahli -ahli rosak untuk mendapatkan faktor umum yang tidak diketahui:

x² (x + 1) + 4 (x + 1) = 0

(x² + 4)_*(x + 1) = 0.

• Dengan cara ini, dua faktor diperoleh, yang mesti sama dengan sifar:

(x² + 4) = 0

(x + 1) = 0.

• Dapat dilihat bahawa faktor (x² + 4) = 0 tidak akan mempunyai penyelesaian sebenar, sementara faktor (x + 1) = 0 ya. Oleh itu, penyelesaiannya ialah:

(x + 1) = 0

x = -1.

Latihan yang diselesaikan

Selesaikan persamaan berikut:

Latihan pertama

(2x² + 5)_*(X - 3)_*(1 + x) = 0.

Penyelesaian

Dalam kes ini persamaan dinyatakan sebagai pendaraban polinomial; iaitu, ia dipertimbangkan. Untuk menyelesaikannya, setiap faktor mestilah sama dengan sifar:

2x² + 5 = 0, tidak mempunyai penyelesaian.

x - 3 = 0

x = 3.

1 + x = 0

x = - 1.

Dengan cara ini, persamaan yang diberikan mempunyai dua penyelesaian: x = 3 dan x = -1.

Latihan kedua

x⁴ - 36 = 0.

Penyelesaian

Polinomial diberikan, yang boleh ditempatkan semula sebagai perbezaan di dataran untuk mencapai penyelesaian yang lebih cepat. Oleh itu, persamaan tetap:

(x² + 6)_*(x² - 6) = 0.

Untuk mencari penyelesaian persamaan kedua -dua faktor adalah sama dengan sifar:

(x² + 6) = 0, tidak mempunyai penyelesaian.

(x² - 6) = 0

x² = 6

x = ± √6.

Oleh itu, persamaan awal mempunyai dua penyelesaian:

x = √6.

x = - √6.