Unit tenaga bebas gibbs, bagaimana ia dikira, latihan diselesaikan

The Tenaga Percuma Gibbs (biasanya dipanggil g) adalah potensi termodinamik yang ditakrifkan sebagai perbezaan entalpi h, kecuali produk suhu t, oleh entropi s sistem:

G = h - t s

Tenaga Bebas Gibbs diukur dalam joules (mengikut sistem antarabangsa), di ergios (untuk sistem liga unit), kalori atau voltan elektron (Untuk voltan elektro).

Rajah 1. Rajah menunjukkan definisi tenaga Gibbs dan hubungannya dengan potensi termodinamik yang lain. Sumber: kuasa nuklear.jaring.

Dalam proses yang berlaku pada tekanan dan suhu malar, variasi tenaga bebas Gibbs ialah ΔG = ΔH - T ΔS. Dalam proses sedemikian, (g) mewakili tenaga yang terdapat dalam sistem yang boleh menjadi kerja.

Sebagai contoh, dalam tindak balas kimia eksotermik, entalpi berkurangan sementara entropi meningkat. Dalam fungsi Gibbs kedua -dua faktor ini diatasi, tetapi hanya apabila tenaga Gibbs menurunkan tindak balas berlaku secara spontan.

Jadi, jika variasi g adalah negatif, prosesnya adalah spontan. Apabila fungsi Gibbs mencapai minimum, sistem mencapai keseimbangan yang stabil. Ringkasnya, dalam proses yang tekanan dan suhu tetap tetap kita dapat mengesahkan:

- Sekiranya prosesnya spontan, maka ΔG < 0

- Apabila sistem berada dalam keseimbangan: Δg = 0

- Dalam proses bukan spontan, ia meningkat: Δg> 0.

[TOC]

Bagaimana ia dikira?

Gibbs Free Energy (g) dikira dengan definisi yang diberikan pada mulanya:

G = h - t ⋅ s

Sebaliknya, entalpi h adalah potensi termodinamik yang ditakrifkan sebagai:

H = u + p v

- Langkah demi langkah

Seterusnya, analisis langkah -langkah -langkah akan dilakukan, untuk mengetahui pembolehubah bebas yang mana Gibbs Energy adalah fungsi:

1- Undang-undang termodinamik pertama, tenaga dalaman berkaitan dengan entropi sistem dan volumnya V untuk proses yang boleh diterbalikkan melalui hubungan pembezaan:

Ia boleh melayani anda: etidium bromida: struktur, sifat, kegunaan, ketoksikan

Du = DQ - DW = TDS - PDV

Dari persamaan ini ia mengikuti bahawa tenaga dalaman u adalah fungsi pembolehubah s dan v:

U = u (s, v)

2- Bermula dari definisi H dan mengambil perbezaan diperoleh:

dh = du + d (p v) = du + vdp + pdv

3- Menggantikan ungkapan untuk DU yang diperolehi dalam (1) anda perlu:

DH = TDS - PDV + VDP + PDV = TDS + VDP

Dari sini disimpulkan bahawa entalpi h bergantung kepada entropi dan tekanan p, iaitu:

H = h (s, p)

4- Sekarang jumlah pembezaan tenaga bebas Gibbs dikira memperoleh:

Dg = dh -tds -sdt = tds + vdp -tds -sdt

Di mana DH telah digantikan dengan ungkapan yang terdapat dalam (3).

5- Akhirnya, dengan memudahkan anda mendapatkan: DG = VDP - SDT, Sudah jelas bahawa tenaga bebas g bergantung kepada tekanan dan suhu T sebagai:

G = g (p, t)

- Hubungan termodinamik Maxwell

Dari analisis di bahagian sebelumnya, ia mengikuti bahawa tenaga dalaman sistem adalah fungsi entropi dan kelantangan:

U = u (s, v)

Kemudian perbezaan Atau menjadi:

du = ∂_SU |_V DS + ∂_VU |_S Dv = tds - pdv

Dari ungkapan ini dalam derivatif separa, hubungan thermodinamik Maxwell yang disimpulkan dapat disimpulkan. Derivatif separa dikenakan apabila fungsi bergantung kepada lebih daripada satu pemboleh ubah dan mudah dikira dengan menggunakan teorem bahagian berikut.

Hubungan pertama Maxwell

 ∂_VT |_S = -Mon_SP |_V 

Untuk mendapatkan hubungan ini, Teorem Clairaut - Schwarz Mengenai derivatif separa, yang menyatakan perkara berikut:

"Derivatif campuran pesanan kedua dengan pembolehubah yang ditukar adalah sama, dengan syarat fungsi yang diperolehi adalah berterusan dan berbeza".

Hubungan kedua Maxwell

Bermula dari apa yang ditunjukkan dalam titik 3 bahagian sebelumnya:

Boleh melayani anda: faktor yang mempengaruhi kelarutan

H = H (S, P) dan DH = TDS + VDP

Boleh didapati:

 ∂_PT |_S = ∂_SV |_P 

Teruskan dengan cara yang sama dengan Gibbs Free Energy G = g (p, t) Dan dengan tenaga bebas Helmholtz F = f (t, v) Untuk mendapatkan dua hubungan termodinamik yang lain di Maxwell. 

Rajah 2. Josiah Gibbs (1839-1903) adalah ahli fizik, ahli kimia dan ahli matematik Amerika yang memberikan sumbangan besar kepada termodinamik. Sumber: Wikimedia Commons.

Hubungan empat termodinamik Maxwell 

1- dikaitkan dengan tenaga dalaman u: ∂_VT |_S = -Mon_SP |_V

2- Yang diperoleh dari entalpi h: ∂_PT |_S = ∂_SV |_P 

3- Berkaitan dengan tenaga Helmholtz F: ∂_TP |_V = ∂_VS |_T 

4- Dihubungkan dengan Tenaga Percuma Gibbs G: ∂_TV |_P = -Mon_PS |_T

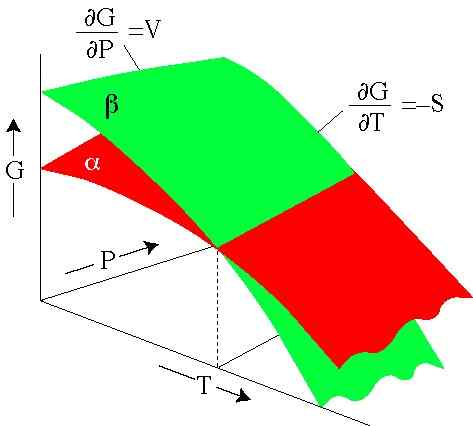Rajah 2. Tenaga Gibbs bergantung pada tekanan dan suhu. Setiap permukaan mewakili fasa. (SERC.Carleton.Edu)

Latihan yang diselesaikan

Latihan 1

Kirakan variasi tenaga bebas Gibbs untuk 2 tahi gas ideal pada suhu 300k semasa pengembangan isoterma yang membawa kepada sistem isipadu awal 20 liter ke jumlah akhir 40 liter.

Penyelesaian

Mengingat definisi tenaga bebas Gibbs adalah:

G = h - t s

Maka variasi f yang terhingga akan menjadi:

ΔG = ΔH - T ΔS, Sejak Δt = 0

Dalam entalpi gas ideal hanya bergantung pada suhu mutlaknya, tetapi kerana ia adalah proses isoterma, maka ΔH = 0 dan ΔG = - T ΔS.

Untuk gas ideal, variasi entropi proses isoterma adalah: 

ΔS = nr ln (v₂/V₁)

Yang digunakan untuk kes latihan ini kita ada:

ΔS = 2 moles x 8,314 j/(k mol) x ln (40L/20L) = 11.53 J/k

Kemudian kita boleh mendapatkan perubahan dalam tenaga Helmholtz:

ΔG = - 300k x 11.53 j/k = -3457.70 j.

Latihan 2

Mengambil kira bahawa tenaga bebas Gibbs adalah fungsi suhu dan tekanan g = g (t, p); Tentukan variasi g semasa proses di mana suhu tidak berubah (isotermal) untuk n moles gas monoatomik yang ideal.

Boleh melayani anda: strontium hidroksida (sr (OH) ₂)

Penyelesaian

Seperti yang ditunjukkan di atas, perubahan tenaga Gibbs hanya bergantung kepada perubahan suhu T dan volum V, jadi variasi yang sangat kecil itu dikira mengikut:

Dg = -sdt + vdp

Tetapi jika ia adalah proses di mana suhu adalah malar maka df = + VDP, jadi variasi tekanan yang terhingga ΔP membawa kepada perubahan dalam tenaga Gibbs yang diberikan oleh:

ΔG = + ∫ vdp = + ∫ (n r t) dp/p = + n r t ln (Δp)

Menggunakan persamaan gas yang ideal:

P v = n r t

Semasa proses isoterma ia berlaku:

D (p v) = p dv + v dp = 0

Itu dia:

dp/p = - dv/v

Jadi hasil sebelumnya boleh ditulis bergantung pada variasi kelantangan ΔV:

ΔG = + ∫ vdp = + ∫ (n r t) dp/p = - ∫ (n r t) dv/v = -n r t ln (ΔV)

Latihan 3

Memandangkan tindak balas kimia berikut:

N₂0 (g) + (3/2) atau₂ (g) ↔️No₂ (g) pada suhu t = 298 k

Cari variasi tenaga bebas Gibbs dan melalui hasil yang diperoleh, tunjukkan sama ada ia adalah proses spontan.

Penyelesaian

Di bawah langkah -langkah:

- Langkah pertama: enthalpi reaksi

ΔHr = 2*ΔH (tidak₂ (g)) - ΔH (n₂0 (g)) = 2*33.2-81.6 = -15.2kj/mol

- Langkah kedua: Variasi entropi reaksi

ΔSR = 2*s (tidak₂ (g)) - s (n₂0 (g)) - (3/2) s (atau₂ (g)) = 2*240.1 - 220.1 - 1.5*205.2 = -47.7 j/(mol*k).

- Langkah Ketiga: Perubahan dalam fungsi Gibbs

Nilai ini akan menentukan keseimbangan antara penurunan tenaga dan meningkatkan entropi untuk mengetahui sama ada tindak balas akhirnya spontan atau tidak.

Δgr = ΔHr -t ΔSr = -15.2 -298*(-47.7) = -985.4 J/mol

Kerana ia adalah variasi negatif tenaga Gibbs, dapat disimpulkan bahawa ia adalah tindak balas spontan pada suhu 298 k = 25 ºC.

Rujukan

1. Castaños e. Latihan Tenaga Percuma. Pulih dari: lidiaconlachimica.WordPress.com.
2. Cengel, dan. 2012. Thermodynamics. Edisi ke -7. McGraw Hill.
3. Libretxts. Tenaga Percuma Gibbs. Pulih dari: chem.Libretxts.org
4. Libretxts. Apa itu Tenaga Percuma. Pulih dari: chem.Libretxts.org
5. Wikipedia. Tenaga Percuma Gibbs. Pulih dari: Adakah.Wikipedia.com
6. Wikipedia. Tenaga Percuma Gibbs. Diperoleh dari: dalam.Wikipedia.com