Formula keseimbangan putaran dan persamaan, contoh, latihan

Dikatakan bahawa badan lanjutan ada keseimbangan putaran Apabila jumlah tork yang bertindak di atasnya adalah sifar. Ini tidak bermaksud bahawa objek itu semestinya berehat, tetapi tidak ada trend bersih untuk mengubah keadaan pergerakannya ke yang lain.

Objek yang bergerak dengan kelajuan tetap melakukannya di sepanjang garis lurus dan kita dapat menganggapnya dalam keseimbangan putaran. Sekarang, objek berputar kerana ada daya yang bertindak pada mereka sedemikian rupa sehingga ia adalah putaran. Keupayaan daya untuk menghasilkan putaran, dipanggil tork atau Torca, Ia bergantung bukan sahaja pada intensiti daya, tetapi juga di mana ia digunakan.

Rajah 1. Jambatan penggantungan angka itu direka untuk menjadi keseimbangan putaran. Sumber: Wikimedia Commons.

Kami mengenali ini dengan serta -merta apabila pintu tertutup akan dibuka: daya tidak pernah digunakan berhampiran engsel, tetapi jauh dari mereka, jadi pemegangnya diletakkan sejauh mungkin, di sebelah pintu pintu.

Engsel melepasi paksi putaran pintu. Bergegas untuk menolaknya sangat dekat dengan engsel, anda perlu berusaha keras untuk pintu untuk bergerak sedikit.

Dalam kesusasteraan adalah tork dengan nama yang berbeza: momen kilasan, kilasan, momen daya dan torca. Semua adalah sinonim.

Oleh itu, kita perlu mengetahui tork yang bertindak pada objek untuk menetapkan keadaan keseimbangan putaran.

[TOC]

Keadaan keseimbangan putaran

Keadaan keseimbangan putaran adalah:

Jumlah semua momen atau tork yang bertindak pada badan, dikira berkenaan dengan mana -mana paksi, mesti tidak sah.

Objek yang dipersoalkan mesti dilanjutkan, kerana zarah, mengikut definisi, hanya mempunyai baki terjemahan.

Anda boleh melayani anda: Undang -undang Kedua Newton: Aplikasi, Eksperimen dan Latihan

Mungkin ada daya yang digunakan di badan dan masih ada keseimbangan putaran, sementara daya tidak mengubahnya.

Mungkin juga ada pergerakan, bahkan dipercepat, tetapi selalu di sepanjang garis lurus, kerana tidak semua daya menyebabkan penampilan tork. Ini muncul apabila kekuatan tidak bertindak sepanjang garis tindakan yang sama.

Tork atau momen kekuatan

Tork dilambangkan dengan lirik Yunani τ, dalam Font Bold Kerana ia adalah vektor dan kita membezakannya dari magnitud atau modulnya, yang merupakan skalar. Ia bergantung pada daya yang digunakan F, vektor r yang diarahkan dari paksi putaran atau ke titik penggunaan daya dan akhirnya, sudut antara kedua -dua vektor ini.

Hubungan yang betul antara magnitud ini ditubuhkan melalui produk vektor:

τ = r x F

Dan modul tork, dilambangkan tanpa berani adalah:

τ = r ⋅f ⋅sen θ

Di mana θ adalah sudut antara r dan F. Unit tork hanya n dalam sistem antarabangsa.

Dalam angka terdapat kunci bahasa Inggeris yang dimaksudkan. Untuk ini, dua kuasa dicuba F_Ke dan F_B.

F_Ke lebih dekat dengan o dan mempunyai vektor r_Ke atau lengan tuil yang lebih pendek, oleh itu tidak menghasilkan banyak tork dan daya F_B, Yang mempunyai magnitud yang sama, tetapi ia mempunyai vektor r_B lebih besar.

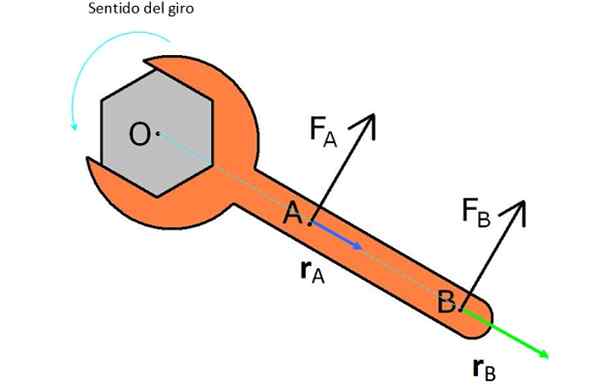Rajah 2. Angkatan dan lengan yang digunakan untuk kunci bahasa Inggeris untuk menjadikannya bertentangan dengan jarum jam. Sumber: Wikimedia Commons.

Perhatikan bahawa jika anda ingin memutar kacang dalam jadual, anda perlu memohon kuasa ke arah yang bertentangan dengan cara mereka muncul dalam angka tersebut.

Arah dan rasa tork

Oleh kerana tork hasil dari produk silang antara kekuatan dan vektor kedudukan, dan ini berada dalam satah kunci bahasa Inggeris, tork harus menjadi vektor yang berserenjang dengan satah itu, iaitu, diarahkan ke pembaca atau di dalam halaman.

Boleh melayani anda: tekanan atmosfera: nilai normal, bagaimana ia diukur, contohnya

Oleh konvensyen, tork adalah positif jika ia menghasilkan giliran ke arah yang bertentangan dengan jarum jam, dan negatif jika ia berbuat demikian ke arah jam.

Arah dan arah tork yang dihasilkan mudah ditentukan oleh peraturan tangan kanan yang ditunjukkan di bawah:

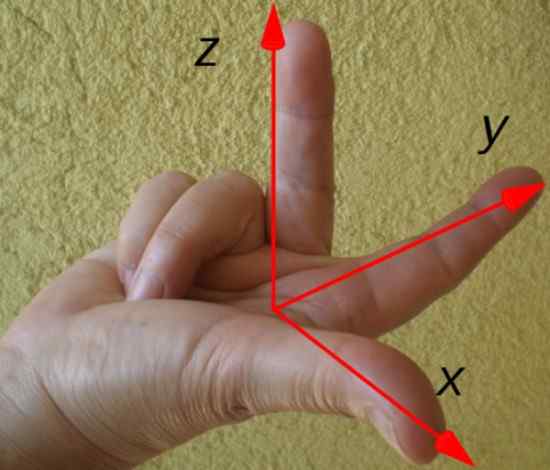Rajah 3. Peraturan tangan kanan untuk menentukan arah dan arah Troca. Sumber: Wikimedia Commons.

Titik jari telunjuk mengikut vektor kedudukan r, Jari tengah mengikut kekerasan F Dan ibu jari menandakan arah dan arah tork τ. Dalam contoh ini, tork diarahkan sepanjang paksi x, mengikut lukisan paksi koordinat.

Formula dan persamaan

Sekiranya tork bertindak pada badan τ₁, τ_2, τ_3… τ_Yo, Tork bersih atau terhasil τ_n Ia adalah jumlah vektor dari mereka semua:

τ_n = τ₁+ τ₂ +  τ₃ +_… τ_Yo

Dengan penjumlahan penjumlahan ia tetap:

τ_n = Σ τ_Yo

Keadaan keseimbangan dinyatakan secara matematik seperti berikut:

τ_n = 0

Wahai:

Σ τ_Yo = 0

Di mana tork τ, Mengenai paksi O tertentu, ia dikira oleh:

τ = r x F

Dan magnitudnya:

τ = r ⋅f ⋅sen θ

Contoh

-Pada manusia dan haiwan, berat badan adalah daya yang boleh menyebabkan tork dan giliran dan jatuh.

Orang biasanya mengekalkan kedudukan sedemikian rupa ketika berjalan, membuatkan mereka dalam keseimbangan putaran, kecuali aktiviti sukan diamalkan, seperti gimnastik, skating atau sukan secara umum.

-Dua anak yang berjaya mendatar di Rocker Sama ada atas dan bawah Mereka berada dalam keseimbangan putaran.

-Apabila piring keseimbangan seimbang, sistem berada dalam keseimbangan putaran.

-Notis dan lampu isyarat yang digantung di jalanan dan jalan juga dalam keseimbangan putaran. Sekiranya kabel yang memegangnya rosak, keseimbangan ini hilang dan notis itu tergantung atau jatuh.

Ia dapat melayani anda: pecutan purata: bagaimana ia dikira dan diselesaikan

-Jambatan Gantung seperti Golden Gate di San Francisco dan Jambatan Rajah 1.

Latihan diselesaikan

Bar yang disokong oleh sokongan yang ditunjukkan dalam angka itu sangat ringan. Daya yang diberikan oleh sokongan adalah F dan pada akhirnya daya berlaku Ke.

Diminta untuk mengira magnitud daya ini memandangkan sistem itu berada dalam keseimbangan terjemahan dan putaran.

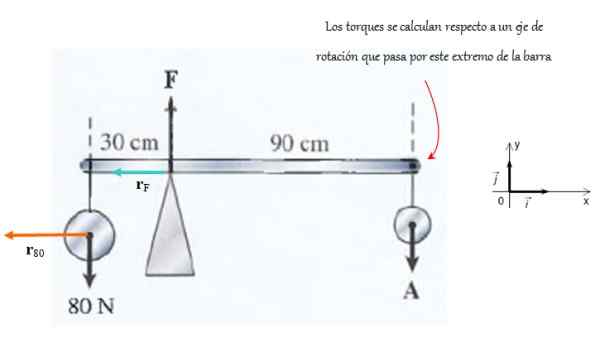Rajah 4. Di bar ini bertindak sedemikian rupa sehingga ia kekal dalam keseimbangan putaran. Sumber: f. Zapata.

Penyelesaian

Oleh kerana sistem tidak bergerak, jumlah kuasa dibatalkan. Semuanya menegak dan anda boleh bekerja dengan magnitud. Perasaan positif semakin meningkat dan negatif, oleh itu:

F - 80 - A = 0

Sekarang keadaan keseimbangan putaran digunakan, yang mana anda perlu memilih paksi putaran sewenang -wenang. Dalam kes ini ia dipilih di hujung kanan, supaya vektor r_Ke Jadilah batal, dengan cara ini tork dilaksanakan oleh Ke, tetapi hanya orang -orang F dan kekuatan kiri.

Tork yang dihasilkan oleh F Ia adalah, mengikut peraturan tangan kanan dan sistem koordinat yang ditunjukkan:

τ_F = r_F x F = 0.9 f (-k) N.m

Ia diarahkan ke dalam skrin dan mempunyai tanda negatif. Walaupun tork yang dihasilkan oleh kekuatan 80 n ialah:

τ = 80 x 1.dua puluh (k) N ⋅ m = 96 (k) N

Tork ini diarahkan dari skrin dan diberikan tanda positif. Kerana terdapat keseimbangan putaran:

96 - 0.9 ⋅F = 0

Magnitud F adalah:

F = (96/0.9) n = 106.7 n

Dan kerana sistem dalam baki terjemahan, jumlah kuasa dibatalkan. Ini membolehkan kita membersihkan magnitud Ke:

F - A - 80 N = 0

Oleh itu:

A = 106.7 - 80 n = 26.7 n.

Rujukan

1. Rex, a. 2011. Asas Fizik. Pearson.
2. Serway, r., Jewett, J. (2008). Fizik untuk Sains dan Kejuruteraan. Jilid 1. Ke -7. Ed. Pembelajaran Cengage.
3. Sears, Zemansky. 2016. Fizik universiti dengan fizik moden. Ke -14. Ed. Jilid 1. Pearson.
4. Tipler, ms. (2006) Fizik untuk Sains dan Teknologi. Edisi ke -5. Jilid 1. Editorial kembali.
5. Tippens, ms. 2011. Fizik: Konsep dan aplikasi. Edisi ke -7. McGraw Hill.