Penentuan Baki Translasi, Aplikasi, Contoh

Dia Keseimbangan translasi Ini adalah keadaan di mana objek secara keseluruhan adalah apabila semua kuasa yang bertindak di atasnya dikompensasi, mengakibatkan kekuatan yang tidak sah. Secara matematik ia bersamaan dengan mengatakan bahawa f₁+ F₂ +  F₃ +… . = 0, menjadi f₁, F₂,  F₃... pasukan yang terlibat.

Hakikat bahawa badan dalam keseimbangan translasi tidak bermaksud bahawa ia semestinya berehat. Ini adalah kes tertentu definisi sebelumnya. Objek boleh bergerak, tetapi jika tiada pecutan, ini akan menjadi pergerakan rectilinear seragam.

Rajah 1. Baki terjemahan adalah penting untuk sebilangan besar sukan. Sumber: Pixabay.

Jadi jika badan berehat terus. Dan jika anda sudah mempunyai pergerakan, ia akan mempunyai kelajuan yang berterusan. Secara umum, pergerakan mana -mana objek adalah komposisi terjemahan dan putaran. Terjemahan boleh seperti yang ditunjukkan dalam Rajah 2: linear atau curvilinear.

Tetapi jika salah satu titik objek ditetapkan, maka satu -satunya kemungkinan bergerak adalah berputar. Contoh ini adalah CD, yang pusatnya tetap. CD mempunyai kemungkinan untuk berputar di sekitar paksi yang melewati titik itu, tetapi tidak bergerak.

Apabila objek mempunyai titik tetap atau disokong di permukaan, ada perbincangan mengenai pautan. Pautan berinteraksi mengehadkan pergerakan yang mampu dibuat oleh objek.

[TOC]

Penentuan keseimbangan translasi

Untuk zarah secara seimbang adalah sah untuk memastikan bahawa:

F_R = 0

Atau dalam ringkasan notasi:

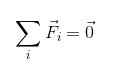
Jelas bahawa untuk badan berada dalam keseimbangan translasi, daya yang bertindak di atasnya mesti diberi pampasan dalam beberapa cara, sehingga hasilnya tidak sah.

Dengan cara ini objek tidak akan mengalami pecutan dan semua zarahnya berada di rehat atau eksperimen terjemahan rectilinear dengan kelajuan tetap.

Ia dapat melayani anda: Teori Big Bang: Ciri -ciri, Tahap, Bukti, Masalah

Sekarang, jika objek boleh berubah, mereka biasanya akan melakukannya. Itulah sebabnya kebanyakan pergerakan terdiri daripada kombinasi terjemahan dan putaran.

Putaran objek

Apabila keseimbangan putaran adalah penting, mungkin perlu untuk memastikan objek itu tidak berubah. Kemudian anda perlu belajar sama ada terdapat tork atau detik -detik yang bertindak di atasnya.

Tork adalah magnitud vektor di mana putaran bergantung. Memerlukan agar daya digunakan, tetapi titik permohonan ini juga penting. Untuk menjelaskan idea itu, pertimbangkan objek lanjutan di mana daya bertindak F Dan mari kita lihat jika anda dapat menghasilkan putaran berkenaan dengan beberapa paksi atau.

Sudah intuited bahawa dengan menolak objek pada titik p dengan daya F, Adalah mungkin untuk menghidupkan titik o, dengan arah anti -horari. Tetapi arah di mana daya digunakan juga penting. Contohnya daya yang digunakan dalam angka medium tidak akan dapat mengubah objek, walaupun ia pasti dapat memindahkannya.

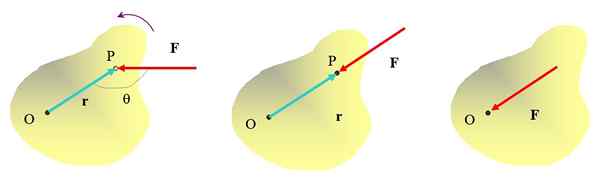Rajah 2. Pelbagai cara untuk memohon daya pada objek yang luas, hanya dalam angka yang melampau kiri kesan putaran diperolehi. Sumber: Diri Diri.

Gunakan daya secara langsung pada titik atau tidak akan digunakan untuk menghidupkan objek sama ada. Kemudian jelas bahawa untuk mencapai kesan putaran, daya mesti digunakan pada jarak tertentu dari paksi putaran dan garis tindakannya tidak boleh melalui paksi itu.

Definisi tork

Tork atau momen daya, dilambangkan sebagai τ magnitud vektor yang bertanggungjawab untuk meletakkan semua fakta ini bersama -sama, ditakrifkan sebagai:

τ = r x f

Vektor r Ia diarahkan dari paksi putaran ke titik penggunaan daya dan penyertaan sudut antara r dan f adalah penting. Oleh itu, magnitud tork dinyatakan sebagai:

Boleh melayani anda: Undang -undang pertama Newton: formula, eksperimen dan latihan

τ = r.F.Sen q

Tork yang paling berkesan berlaku ketika r dan F Mereka berserenjang.

Sekarang, jika dikehendaki bahawa tiada putaran atau lulus ini dengan pecutan sudut yang berterusan, adalah perlu bahawa jumlah tork yang bertindak pada objek itu adalah batal, sama dengan apa yang dipertimbangkan untuk kuasa:

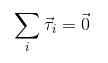
Keadaan keseimbangan

Keseimbangan bermaksud kestabilan, keharmonian dan keseimbangan. Agar pergerakan sesuatu objek memiliki ciri -ciri ini, syarat -syarat yang diterangkan dalam bahagian sebelumnya mesti digunakan:

1) f₁+ F₂ +  F₃ +… . = 0

2) τ₁+ τ₂ +  τ₃ +… . = 0

Keadaan pertama menjamin keseimbangan translasi dan yang kedua adalah putaran. Kedua -duanya mesti dipenuhi jika objek itu mahu kekal baki statik (ketiadaan pergerakan apa -apa jenis).

Aplikasi

Keadaan keseimbangan boleh digunakan untuk pelbagai struktur, kerana apabila bangunan atau pelbagai objek dibina, dibuat dengan niat bahawa bahagian mereka dikekalkan dalam kedudukan relatif yang sama antara satu sama lain. Dengan kata lain, objek itu tidak dilucutkan.

Ini penting misalnya ketika membina jambatan yang tetap kukuh di bawah kaki mereka, atau ketika merancang struktur yang dapat dihuni yang tidak mengubah kedudukan atau mempunyai kecenderungan untuk membuang.

Walaupun dipercayai bahawa pergerakan rectilinear seragam adalah penyederhanaan pergerakan yang melampau, yang biasanya berlaku sedikit, harus diingat bahawa kelajuan cahaya dalam kekosongan adalah tetap, dan bunyi di udara juga, jika menganggap homogen dengan persekitaran.

Dalam banyak struktur mudah alih yang dibuat oleh manusia, penting bahawa kelajuan berterusan dikekalkan: contohnya, pada tangga mekanikal dan garis pemasangan.

Ia boleh melayani anda: Undang -undang Termodinamik Kedua: Formula, Persamaan, Contoh

Contoh keseimbangan translasi

Ini adalah latihan ketegangan klasik yang memegang lampu secara seimbang. Diketahui bahawa lampu beratnya 15 kg. Cari magnitud ketegangan yang diperlukan untuk menyimpannya dalam kedudukan ini.

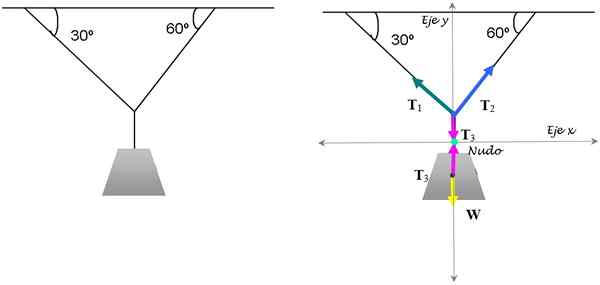Rajah 3. Baki lampu dijamin dengan menggunakan keadaan keseimbangan translasi. Sumber: Diri Diri.

Penyelesaian

Untuk menyelesaikannya, kami memberi tumpuan kepada simpul di mana tiga rentetan bersatu. Gambar rajah badan bebas masing -masing untuk simpulan dan lampu ditunjukkan dalam angka di atas.

Berat lampu adalah W = 5 kg . 9.8 m/s² = 49 n. Untuk lampu itu seimbang, sudah cukup bahawa keadaan keseimbangan pertama dipenuhi:

T₃ - W = 0

T₃ = W = 49 n.

Ketegangan T₁ dan T₂ Mereka mesti terurai:

T_1y + T_{2 dan} - T₃ = 0 (Musim panas kuasa di sepanjang paksi y))

-T_1x +T_2x = 0 (Musim panas kuasa di sepanjang paksi x)

Memohon Trigonometri:

T₁.Cos 60º +t₂ .Cos 30º = 49

- T₁.sen60º +t₂.Sen30º = 0

Ia adalah sistem dua persamaan dengan dua orang yang tidak diketahui, yang jawapannya adalah: T₁ = 24.5 n dan T₂ = 42.4 n.

Rujukan

1. Rex, a. 2011. Asas Fizik. Pearson. 76 - 90.
2. Serway, r., Jewett, J. (2008). Fizik untuk Sains dan Kejuruteraan. Jilid 1. 7^ma. Ed. Pembelajaran Cengage. 120 - 124.
3. Serway, r., Vulle, c. 2011. Asas Fizik. 9^na Ed. Pembelajaran Cengage. 99-112.
4. Tippens, ms. 2011. Fizik: Konsep dan aplikasi. Edisi ke -7. Macgraw Hill. 71 - 87.
5. Walker, J. 2010. Fizik. Addison Wesley. 332 -346.