Formula ralat pensampelan dan persamaan, pengiraan, contoh
- 3657
- 226
- Clarence Greenholt DDS
Dia ralat pensampelan Sama ada Ralat sampel Dalam statistik, ia adalah perbezaan antara nilai purata sampel berkenaan dengan nilai purata jumlah penduduk. Untuk menggambarkan idea itu, mari kita bayangkan bahawa jumlah penduduk bandar adalah satu juta, dari mana anda mahukan kasut purata, yang mana seribu orang diambil secara rawak.
Saiz purata yang timbul daripada sampel tidak semestinya bertepatan dengan jumlah penduduk, walaupun jika sampel tidak berat sebelah, nilai mesti dekat. Perbezaan antara nilai purata sampel dan jumlah penduduk adalah kesilapan sampel.
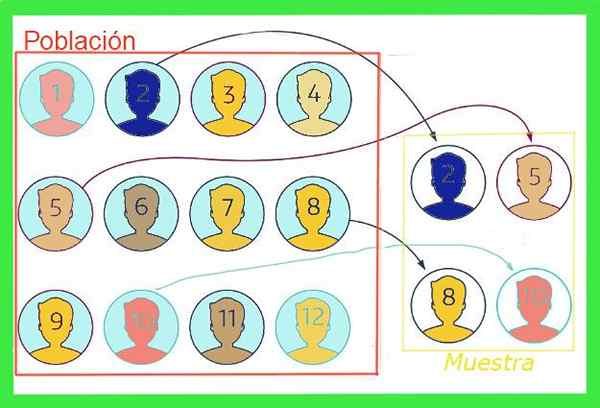
 Rajah 1. Oleh kerana sampel adalah subset dari jumlah penduduk, purata sampel mempunyai margin kesilapan. Sumber: f. Zapata.
Rajah 1. Oleh kerana sampel adalah subset dari jumlah penduduk, purata sampel mempunyai margin kesilapan. Sumber: f. Zapata. Secara umum, nilai purata jumlah penduduk tidak diketahui, tetapi ada teknik untuk mengurangkan kesilapan dan formula tersebut untuk menganggarkan Margin ralat sampel yang akan dipamerkan dalam artikel ini.
[TOC]
Formula dan persamaan
Mari kita letakkan, anda ingin mengetahui nilai purata ciri yang boleh diukur tertentu x Dalam populasi saiz N, tetapi bagaimana N Ia adalah sejumlah besar tidak berdaya maju untuk mengkaji jumlah penduduk, jadi kami terus mengambil a sampel aleatory saiz n<
Nilai purata sampel dilambangkan oleh dan nilai purata jumlah penduduk menandakannya untuk huruf Yunani μ (Ia dibaca Mu atau miu).
Katakan mereka diambil m Jumlah sampel penduduk N, Semua saiz yang sama n Dengan nilai purata
Nilai purata ini tidak akan sama antara satu sama lain dan semuanya akan berada di sekitar nilai populasi purata μ. Dia Margin ralat sampel e menunjukkan pemisahan yang dijangkakan bagi nilai purata berkenaan dengan Nilai populasi purata μ dalam peratusan yang ditentukan dipanggil Tahap Amanah γ (Gamma).
Boleh melayani anda: songsang tambahanDia Margin ralat standard ε sampel saiz n adalah:
ε = σ/√n
di mana σ adalah sisihan piawai (Akar kuadrat varians), yang dikira oleh formula berikut:
σ = √ [(x -)2/(N - 1)]
Maksud Margin ralat standard ε adalah perkara berikut:
Dia nilai pertengahan diperoleh dengan sampel saiz n difahami dalam selang waktu ( - ε, + ε) dengan tahap keyakinan 68.3%.
Cara Mengira Ralat Pensampelan
Di bahagian sebelumnya formula diberikan untuk mencari julat ralat standard sampel n, di mana perkataan standard menunjukkan bahawa ia adalah margin kesilapan dengan keyakinan 68%.
Ini menunjukkan bahawa jika banyak sampel saiz yang sama diambil n, 68% daripadanya akan memberikan nilai purata dalam julat [ - ε, + ε].
Ada peraturan yang mudah, yang disebut Peraturan 68-95-99.7 yang membolehkan kita mencari margin Ralat sampel e Untuk tahap keyakinan 68%, 95% dan 99.7% mudah, kerana margin ini adalah 1ε, 2ε dan 3 ⋅ε masing -masing.
Untuk tahap keyakinan γ
Kalau dia Tahap Amanah γ Ia bukan mana -mana di atas, jadi ralat pensampelan adalah sisihan piawai σ didarab dengan faktor Zγ, yang diperoleh melalui prosedur berikut:
1.- Pertama tahap kepentingan α yang dikira dari Tahap Amanah γ Melalui hubungan berikut: α = 1 - γ
Boleh melayani anda: Teorem Bayes2.- Maka anda mesti mengira nilai 1 - α/2 = (1 + γ)/2, yang sepadan dengan kekerapan normal yang terkumpul antara -∞ dan Zγ, Dalam pengedaran normal atau Gaussian yang ditonjolkan f (z), definisi yang dapat dilihat dalam Rajah 2.
3.- Persamaan diselesaikan F (Zγ) = 1 - α/2 Melalui jadual pengedaran biasa (terkumpul) F, o Melalui aplikasi komputer yang mempunyai fungsi Gaussian songsang yang ditonjolkan F-1.
Dalam kes yang kedua anda ada:
Zγ = g-1(1 - α/2).
4.- Akhirnya, formula ini untuk kesilapan persampelan dengan tahap kebolehpercayaan digunakan γ:
E = Zγ⋅(σ/√n)
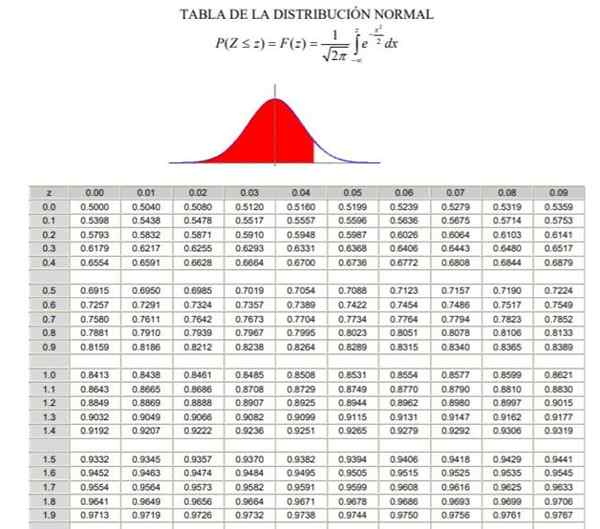 Rajah 2. Jadual pengedaran normal. Sumber: Wikimedia Commons.
Rajah 2. Jadual pengedaran normal. Sumber: Wikimedia Commons. Contoh
- Contoh 1
Kirakan Margin ralat standard Pada purata berat sampel 100 bayi yang baru lahir. Pengiraan berat purata adalah = 3,100 kg dengan sisihan piawai σ = 1,500 kg.
Penyelesaian
Dia Margin ralat standard adalah ε = σ/√n = (1,500 kg)/√100 = 0.15 kg. Yang bermaksud bahawa dengan data ini dapat disimpulkan bahawa berat 68% bayi yang baru lahir antara 2,950 kg dan 3.25 kg.
- Contoh 2
Menentukan margin kesilapan sampel dan dan julat berat 100 bayi baru lahir dengan tahap keyakinan 95% jika berat purata 3,100 kg dengan sisihan piawai σ = 1,500 kg.
Penyelesaian
Jika Kaedah 68; 95; 99.7 → 1 ⋅ε; 2ε; 3 ⋅ε, Kamu ada:
E = 2 ⋅ε = 2 ⋅0.15 kg = 0.30 kg
Dengan kata lain, 95% daripada bayi baru lahir akan mempunyai peso antara 2,800 kg dan 3,400 kg.
- Contoh 3
Tentukan julat peso yang baru lahir dari Contoh 1 dengan margin keyakinan 99.7%.
Boleh melayani anda: rhomboid: ciri -ciri, cara mengeluarkan perimeter dan kawasanPenyelesaian
Ralat sampel dengan keyakinan 99.7% adalah 3 σ/√n, Itu untuk contoh kami ialah E = 3 *0.15 kg = 0.45 kg. Dari sini disimpulkan bahawa 99.7% daripada bayi baru lahir akan mempunyai peso antara 2,650 kg dan 3,550 kg.
- Contoh 4
Tentukan faktor Zγ Untuk tahap kebolehpercayaan sebanyak 75%. Tentukan margin ralat persampelan dengan tahap kebolehpercayaan ini untuk kes yang dibangkitkan dalam Contoh 1.
Penyelesaian
Dia tahap keyakinan adalah γ = 75% = 0.75 yang berkaitan dengan tahap kepentingan α melalui hubungan γ= (1 - α), supaya tahap kepentingan adalah α = 1 - 0.75 = 0.25.
Ini bermaksud bahawa kebarangkalian normal terkumpul antara -∞ dan Zγ adalah:
P (z ≤ Zγ ) = 1 - 0.125 = 0.875
Apa yang sepadan dengan nilai Zγ daripada 1,1503, seperti yang ditunjukkan dalam Rajah 3.
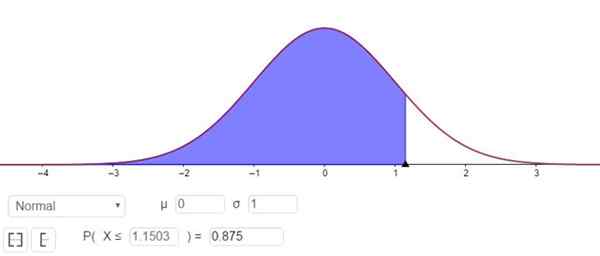 Rajah 3. Penentuan faktor Zγ yang sepadan dengan tahap keyakinan 75%. Sumber: f. Zapata melalui geogebra.
Rajah 3. Penentuan faktor Zγ yang sepadan dengan tahap keyakinan 75%. Sumber: f. Zapata melalui geogebra. Dengan kata lain, ralat pensampelan adalah E = Zγ⋅(σ/√n)= 1.15⋅(σ/√n).
Apabila digunakan untuk Contoh 1 data, ia memberikan ralat:
E = 1.15*0.15 kg = 0.17 kg
Dengan tahap keyakinan 75%.
- Latihan 5
Apakah tahap kepercayaan jika zα/2 = 2.4 ?
Penyelesaian
P (z ≤ zα/2 ) = 1 - α/2
P (z ≤ 2.4) = 1 - α/2 = 0.9918 → α/2 = 1 - 0.9918 = 0.0082 → α = 0.0164
Tahap kepentingan adalah:
α = 0.0164 = 1.64%
Dan akhirnya, tahap kepercayaan tetap:
1- α = 1 - 0.0164 = 100% - 1.64% = 98.36%
Rujukan
- Canavos, g. 1988. Kebarangkalian dan Statistik: Aplikasi dan Kaedah. McGraw Hill.
- DEVORE, J. 2012. Kebarangkalian dan statistik untuk kejuruteraan dan sains. Ke -8. Edisi. Cengage.
- Levin, r. 1988. Statistik untuk pentadbir. 2. Edisi. Prentice Hall.
- Sudman, s.1982. Meminta Soalan: Panduan Praktikal untuk Reka Bentuk Soal Selidik. San Francisco. Jossey Bass.
- Walpole, r. 2007. Kebarangkalian dan statistik untuk kejuruteraan dan sains. Pearson.
- Wonnacott, t.H. dan r.J. Wonnacott. 1990. Statistik Pengenalan. Edisi ke -5. Wiley
- Wikipedia. Ralat sampel. Diperoleh dari: dalam.Wikipedia.com
- Wikipedia. Margin ralat. Diperoleh dari: dalam.Wikipedia.com
- « Sejarah Statistik Inferensi, Ciri -ciri, Apa Itu, Contohnya
- U -TEST OF MANN - WHITNEY Apa yang ada dan ketika terpakai, pelaksanaan, contohnya »

