Usaha biasa apa yang terdiri daripada, bagaimana ia dikira, contohnya

Dia usaha biasa Digunakan untuk bahan tertentu, juga disebut usaha uniaxial, ia adalah hubungan antara daya yang digunakan serenjang ke permukaan tertentu dan kawasan keratan rentas di mana ia bertindak, atau beban per unit kawasan. Secara matematik, jika p adalah magnitud daya dan a adalah kawasan di mana ia digunakan, usaha σ adalah kuota: σ = p/a.

Unit usaha biasa dalam sistem antarabangsa adalah Newton /Metro², Dikenali sebagai Pascal dan Pa Singkat. Ini adalah unit tekanan yang sama. Unit lain yang muncul dalam kesusasteraan sering pound / inci² Sama ada psi.

Rajah 1. Batu -batu sentiasa tertakluk kepada usaha akibat aktiviti tektonik, menyebabkan ubah bentuk di kerak bumi. Sumber: Pixabay.

Dalam Rajah 2, dua daya magnitud yang sama digunakan secara serentak ke kawasan silang -keratan, membuat daya tarikan pada bar yang sangat ringan yang cenderung untuk memanjangkannya.

Pasukan ini menghasilkan usaha biasa yang juga dipanggil Beban paksi berpusat, kerana garis tindakannya bertepatan dengan paksi paksi, di mana centroid terletak.

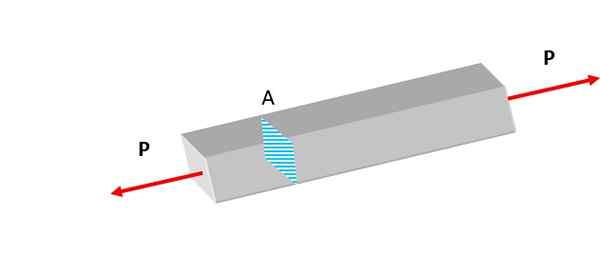Rajah 2. Bar yang ditunjukkan adalah tertakluk kepada daya tarikan. Sumber: Diri Diri.

Usaha, sama ada jenis normal atau lain -lain, kelihatan berterusan. Di litosfera, batuan tertakluk kepada graviti dan aktiviti tektonik, bereksperimen ubah bentuk.

Dengan cara ini struktur seperti lipatan dan kegagalan berasal, yang kajiannya penting dalam penggunaan mineral dan kejuruteraan awam, untuk pembinaan bangunan dan jalan raya, untuk menamakan beberapa contoh.

[TOC]

Bagaimana ia dikira?

Persamaan yang diberikan pada permulaan σ = P/A membolehkan untuk mengira usaha normal purata di kawasan yang dipersoalkan. Nilai P adalah magnitud daya yang dihasilkan di kawasan yang digunakan untuk centroid dan mencukupi untuk banyak situasi mudah.

Dalam kes ini, pengedaran daya seragam, terutamanya pada titik jauh dari mana anda mempunyai bar tertakluk kepada daya tarikan atau mampatan. Tetapi jika usaha itu perlu untuk dikira pada titik tertentu atau kuasa tidak diedarkan sama rata, perlu menggunakan definisi berikut:

Boleh melayani anda: litar elektrik tertutup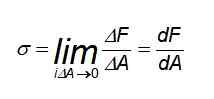

Kemudian secara umum, nilai usaha pada titik tertentu mungkin berbeza dari nilai purata. Sebenarnya usaha itu boleh berbeza mengikut bahagian yang perlu dipertimbangkan.

Ini digambarkan dalam angka berikut, di mana daya tarikan f cuba memisahkan bar dalam keseimbangan di bahagian mm dan nn.

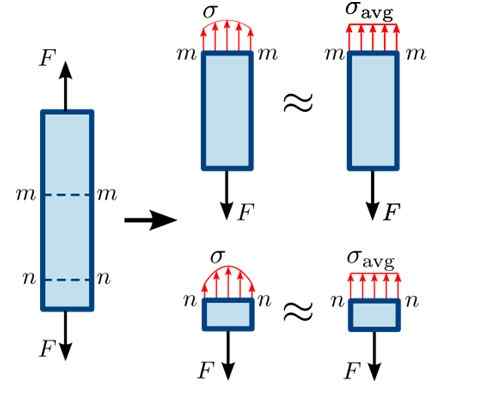Rajah 3. Pengagihan usaha biasa di bahagian bar yang berlainan. Sumber: https: // commons.Wikimedia.org/wiki/fail: normal_stress.Svg#/media/fail: normal_stress.SVG

Sebagai bahagian nn Ia sangat dekat dengan di mana daya turun, pengagihan daya di permukaan tidak sepenuhnya homogen, anak -anak bawah umur ini lebih jauh dari titik itu. Pengagihan sedikit lebih homogen di bahagian mm.

Dalam apa jua keadaan usaha biasa selalu cenderung untuk meregangkan atau memampatkan dua bahagian badan yang terdapat di kedua -dua belah satah di mana mereka bertindak. Sebaliknya, usaha lain yang berbeza, seperti ricih, cenderung bergerak dan memisahkan bahagian -bahagian ini.

Undang -undang Hooke dan usaha biasa

Undang -undang Hooke menyatakan bahawa dalam batas elastik, usaha biasa adalah berkadar terus dengan ubah bentuk yang dialami oleh bar atau objek. Kalau macam itu:

Usaha biasa ∝ ubah bentuk kesatuan

Perpaduan yang berterusan adalah modul muda (y):

Usaha Normal (σ) = Modul Muda (Y) X Deformasi Unsurary (ε)

σ = y. ε

Dengan ε = ΔL/l, di mana ΔL adalah perbezaan antara akhir dan panjang awal, iaitu l.

Modul Modul atau Keanjalan Muda adalah ciri bahan, dimensinya adalah sama dengan usaha itu, kerana ubah bentuk unit tidak dimensi.

Ia boleh melayani anda: 13 contoh undang -undang kedua Newton dalam kehidupan seharian

Kepentingan usaha dalam rintangan bahan dan geologi

Menentukan betapa tahannya bahan -bahan untuk usaha sangat penting. Untuk struktur yang digunakan dalam pembinaan bangunan, serta dalam reka bentuk bahagian untuk peranti yang berbeza, adalah perlu untuk memastikan bahan -bahan yang dipilih dengan betul memenuhi fungsi mereka.

Oleh itu, bahan -bahan dianalisis secara menyeluruh di makmal melalui ujian yang ditakdirkan untuk mengetahui berapa banyak daya yang dapat mereka tolak sebelum ubah bentuk dan pecah, sehingga kehilangan fungsi mereka. Berdasarkan ini, keputusan dibuat sama ada atau tidak untuk mengeluarkan sekeping tertentu atau menjadi sebahagian daripada peranti.

Adalah dipercayai bahawa saintis pertama yang secara sistematik mengkaji rintangan bahan -bahan adalah Leonardo da Vinci. Dia meninggalkan bukti percubaan di mana dia menentukan rintangan wayar yang menggantung batu -batu peso yang berbeza.

Dalam usaha kedua -dua magnitud daya dan juga dimensi struktur dan bagaimana ia digunakan adalah penting, untuk menetapkan had di mana bahan itu mempunyai tingkah laku elastik; iaitu, ia kembali ke bentuk asalnya apabila usaha itu terhenti.

Dengan hasil ujian ini, lengkung pembentukan usaha dilakukan untuk pelbagai jenis bahan, seperti keluli, konkrit, aluminium dan banyak lagi.

Contoh

Dalam contoh -contoh berikut, diandaikan bahawa daya diedarkan secara merata, dan bahan itu homogen dan isotropik. Ini bermaksud bahawa sifatnya adalah sama ke arah mana pun. Oleh itu, sah untuk memohon persamaan σ = p/a untuk mencari usaha.

-Latihan 1

Dalam Rajah 3, diketahui bahawa usaha biasa purata yang bertindak di bahagian AB mempunyai magnitud 48 kPa. Cari: a) Besarnya daya F yang bertindak dalam CB, b) usaha di bahagian BC.

Ia boleh melayani anda: menembak mendatar: ciri, formula dan persamaan, latihan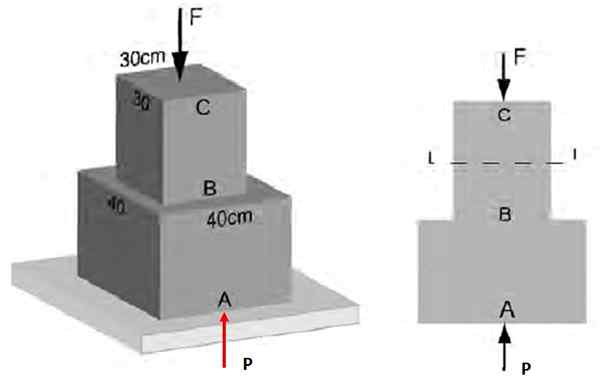Rajah 4. Usaha biasa pada struktur Contoh 1 ..

Penyelesaian

Oleh kerana strukturnya berada dalam keseimbangan statik, menurut undang -undang kedua Newton:

P-f = 0

Usaha biasa di bahagian AB mempunyai magnitud:

σ_Ab = P/a_Ab

Di mana p = σ_Ab . Ke_Ab = 48000 Pa. (40 x 10 ^-2 m)² = 7680 n

Oleh itu f = 7680 n

Usaha biasa di bahagian BC adalah nisbah antara magnitud f dan kawasan bahagian silang di sebelah itu:

σ_BC = F/a_BC = 7680 n / (30 x 10 ^-2 m)² = 85.3 kPa.

-Latihan 2

Wayar 150 m panjang dan 2.Diameter 5 mm diregangkan dengan daya 500 N. Cari:

a) Usaha membujur σ.

b) ubah bentuk kesatuan, mengetahui bahawa panjang akhir adalah 150.125 m.

c) modul keanjalan Dan dari dawai ini.

Penyelesaian

a) σ = f / a = f / π.r²

Radius dawai adalah separuh daripada diameter:

R = 1.25 mm = 1.25 x 10^-3 m.

Kawasan cross -section adalah π.r², Maka usaha itu:

σ = f / π.r² = 500 / (π.(1.25 x 10^-3)² PA = 101859.2 Pa

b) ε = ΔL / L = (Panjang Akhir - Panjang Awal) / Panjang Awal

Oleh itu:

ε = (150.125 - 150) /150 = 0.125/150 = 0.000833

c) Modul muda dawai dibersihkan dengan mengetahui nilai ε dan σ yang dikira sebelum ini:

Y = σ / ε = 101859.2 PA / 0.000833 = 1.22 x 10⁸ PA = 122 mpa.

Rujukan

1. Bir, f. 2010. Bahan mekanik. 5th. Edisi. McGraw Hill. 7 - 9.
2. Giancoli, d.  2006. Fizik: Prinsip dengan aplikasi. 6^tth  Ed. Prentice Hall. 238-242.
3. Hibbeler, R.C. 2006. Bahan mekanik. 6th. Edisi. Pendidikan Pearson. 22 -25
4. Valera Negrete, J. 2005. Nota Fizik Umum. Unam. 87-98.
5. Wikipedia. Tekanan (Mekanik). Pulih dari: wikipedia.org.