Sejarah statistik deskriptif, ciri, contoh, konsep

The Statistik deskriptif Ia adalah cabang statistik yang berkaitan dengan mengumpul dan menganjurkan maklumat mengenai tingkah laku sistem dengan banyak elemen, secara umumnya dikenali sebagai nama penduduk.

Untuk ini, ia menggunakan teknik berangka dan grafik, di mana ia memberikan maklumat, tanpa membuat ramalan atau kesimpulan tentang penduduk di mana ia datang.

Statistik deskriptif dianggap menyusun dan mengemukakan maklumat dengan mudah

[TOC]

Sejarah

Berusia

Statistik mempunyai asal -usulnya dalam keperluan manusia untuk mengatur maklumat yang diperlukan untuk kelangsungan hidup dan kesejahteraannya, serta menyediakan peristiwa yang mempengaruhinya. Tamadun Besar Antiquity meninggalkan rekod peneroka, cukai yang dikumpulkan, jumlah tanaman dan saiz tentera.

Sebagai contoh, semasa pemerintahannya yang panjang, Ramses II (1279-1213 hingga.C) mengarahkan banci tanah dan penduduk di Mesir, yang pada masa itu mempunyai kira -kira 2 juta penduduk.

Begitu juga, Alkitab bahawa Musa melaksanakan banci untuk mengetahui berapa banyak askar yang mempunyai dua belas suku Israel.

Juga dalam tuduhan kuno orang dan sumber kuno dibuat. Orang Roma, yang terkenal dengan organisasi mereka yang tinggi, mendaftarkan penduduk secara berkala, menyediakan banci setiap lima tahun, termasuk wilayah dan sumber.

Renaissance

Selepas kemerosotan Rom, rekod statistik penting takut, sehingga ketibaan Renaissance, ketika statistik kembali.

Memuncak abad ke -17, teori kebarangkalian dilahirkan, hasil kecenderungan orang untuk perjudian, yang memberikan statistik keteguhan matematik yang menjadikannya sains sendiri.

Zaman Moden

Dorongan baru datang dengan teori kesilapan dan dataran minimum pada abad kesembilan belas, yang mengikuti kaedah korelasi antara pembolehubah, secara kuantitatif menilai hubungan antara mereka.

Sehingga akhirnya, pada abad kedua puluh, statistik diperluaskan kepada setiap cabang sains dan kejuruteraan sebagai alat yang sangat diperlukan dalam menyelesaikan masalah.

Ciri -ciri statistik deskriptif

Statistik deskriptif dicirikan oleh:

- Susun maklumat yang dikumpulkan dalam data dan grafik. Grafik boleh beragam: histogram, poligon kekerapan, gambarajah berbentuk kek, antara lain.

- Mengedarkan data dalam julat frekuensi untuk memudahkan pengurusan mereka. Gunakan aritmetik untuk mencari nilai yang paling mewakili data, melalui langkah kecenderungan pusat, serta menganalisis penyebarannya.

- Tentukan bentuk pengagihan, simetri mereka, jika mereka berpusat atau berat sebelah, dan jika mereka ditunjuk atau agak diratakan.

Boleh melayani anda: derivatif tersirat: bagaimana mereka diselesaikan dan diselesaikan latihan

Apakah statistik deskriptif untuk?

Bila -bila masa perlu.

Kemudian kami menyebut beberapa contoh:

Ekonomi

Statistik deskriptif berkaitan dengan mendaftarkan dan menganjurkan data mengenai populasi dan umur mereka, pendapatan, pelaburan, keuntungan dan perbelanjaan. Dengan cara ini kerajaan dan institusi merancang penambahbaikan dan melabur dengan sewajarnya.

Dengan bantuan anda, anda memantau pembelian, jualan, pulangan dan kecekapan perkhidmatan. Atas sebab ini, statistik sangat diperlukan dalam membuat keputusan.

Fizik dan Mekanikal

Fizik dan mekanik menggunakan statistik untuk kajian media berterusan, yang terdiri daripada sejumlah besar zarah, seperti atom dan molekul. Ternyata tidak mungkin untuk memantau masing -masing secara berasingan.

Tetapi mengkaji tingkah laku global sistem (bahagian gas, contohnya) dari sudut pandangan makroskopik, adalah mungkin untuk mengetahui purata dan menentukan pembolehubah makroskopik untuk mengetahui sifatnya. Contohnya ialah teori kinetik gas.

Ubat

Ini adalah alat penting ketika memantau penyakit, dari asal -usulnya dan semasa evolusinya, serta keberkesanan rawatan.

Statistik yang menggambarkan kadar morbiditi, penyembuhan, masa inkubasi atau perkembangan penyakit, umur di mana ia biasanya muncul dan data gaya, diperlukan apabila merancang rawatan yang paling berkesan.

Pemakanan

Salah satu daripada banyak aplikasi statistik deskriptif adalah untuk mendaftarkan dan memerintahkan data mengenai penggunaan makanan dalam populasi yang berbeza: kuantiti, kualiti dan yang paling banyak dimakan, di antara banyak pemerhatian lain bahawa pakar minat.

Contoh statistik deskriptif

Di bawah ini kita akan melihat beberapa contoh yang menggambarkan betapa bergunanya alat statistik deskriptif untuk membantu membuat keputusan:

Contoh 1

Untuk meningkatkan bilik makan sekolah, maklumat pengguna diperlukan. Sumber: Wikimedia Commons.

Pihak berkuasa pendidikan pelan negara penambahbaikan institusi. Katakan mereka akan melaksanakan sistem bilik makan sekolah baru.

Untuk ini adalah perlu mempunyai data mengenai populasi pelajar, contohnya bilangan pelajar setiap gred, umur, jantina, ketinggian, berat dan keadaan sosio -ekonomi mereka. Kemudian maklumat ini dibentangkan dalam bentuk jadual dan graf.

Contoh 2

Untuk memantau pasukan bola sepak tempatan dan membuat penandatanganan baru, pengurus membawa bilangan perlawanan yang dimainkan, dimenangi, terikat dan hilang, serta jumlah gol, pencetak gol dan bagaimana mereka berjaya menjaringkan gol: tendangan bebas, dari setengah mahkamah, penalti, dengan kaki kiri atau kanan, antara butiran lain.

Ia boleh melayani anda: Peristiwa yang saling eksklusif: Contoh dan Contohnya

Contoh 3

Kedai ais krim mempunyai beberapa perisa ais krim dan ingin meningkatkan jualan mereka, oleh itu pemilik menjalankan kajian di mana mereka mengira bilangan pelanggan, memisahkannya ke dalam kumpulan dengan seks dan umur.

Dalam kajian ini, rasa ais krim kegemaran dan persembahan jualan terbaik dicatatkan, sebagai contoh. Dan dengan data yang dikumpulkan, mereka merancang pembelian perisa dan bekas dan aksesori yang diperlukan untuk penyediaannya.

Konsep asas statistik deskriptif

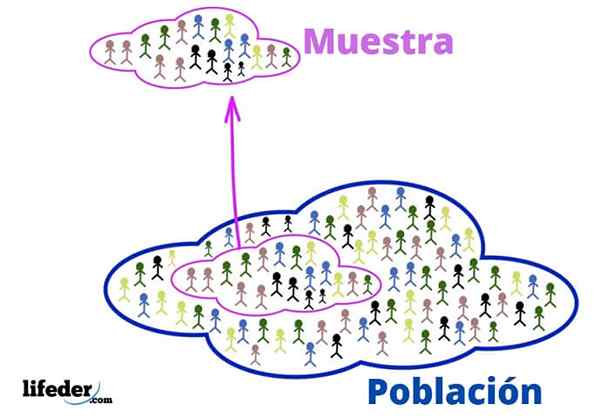Penduduk dan sampel

Konsep -konsep asas ini diperlukan untuk menggunakan teknik statistik, mari kita lihat:

Penduduk

Dalam konteks statistik penduduk merujuk kepada alam semesta atau kolektif dari mana maklumat itu datang.

Ia tidak selalu mengenai orang, kerana mereka boleh menjadi set haiwan, tumbuhan atau objek seperti kereta, atom, molekul, dan juga peristiwa dan idea.

Contoh

Apabila penduduknya sangat besar, sampel wakil diekstrak daripadanya dan dianalisis, tanpa kehilangan maklumat yang relevan.

Ia boleh dipilih secara rawak, atau mengikut beberapa kriteria yang ditubuhkan oleh penganalisis. Kelebihannya ialah menjadi subset penduduk, ia lebih mudah diurus.

Pembolehubah

Ia merujuk kepada set nilai yang boleh mengambil ciri -ciri tertentu penduduk. Kajian mungkin mengandungi pelbagai pembolehubah, seperti umur, jantina, berat badan, tahap akademik, status sivil, pendapatan, suhu, warna, masa dan banyak lagi.

Pembolehubah boleh menjadi sifat yang berbeza, jadi ada kriteria untuk mengklasifikasikannya dan memberi mereka rawatan yang paling sesuai.

Pembolehubah kategori dan pembolehubah berangka

Mengikut cara mereka diukur, pembolehubah boleh:

-Kategori

-Berangka

Pembolehubah kategori, juga dipanggil kualitatif, Mereka mewakili kualiti seperti status sivil seseorang, yang boleh menjadi bujang, berkahwin, bercerai atau janda.

Sebaliknya, kepada pembolehubah berangka atau kuantitatif, Mereka boleh diukur, seperti umur, masa, berat badan, pendapatan dan banyak lagi.

Grafik sangat penting untuk membentangkan maklumat, kerana sekilas trend data dihargai. Sumber: PIQSELS.

Pembolehubah pemboleh ubah yang diskret dan berterusan

Pemboleh ubah diskret hanya mengambil nilai diskret, seperti namanya. Contoh mereka adalah bilangan anak keluarga, berapa banyak subjek dalam kursus tertentu dan jumlah kereta di tempat letak kereta.

Pembolehubah ini tidak selalu mengambil nilai keseluruhan, kerana terdapat juga pecahan.

Sebaliknya, pembolehubah berterusan mengakui nilai tak terhingga dalam julat tertentu, seperti berat seseorang, pH darah, masa konsultasi telefon dan diameter bola bola sepak.

Boleh melayani anda: simetri

Langkah kecenderungan pusat

Memberi idea trend umum yang mengikuti data. Kami akan menyebutkan tiga langkah pusat yang paling banyak digunakan:

-Separuh

-Median

-Fesyen

Separuh

Bersamaan dengan nilai purata. Ia dikira dengan menambahkan semua pemerhatian dan membahagikan antara jumlah keseluruhan:

 Di mana x_Yo Itu adalah pemerhatian dan n adalah jumlahnya.

Fesyen

Ia adalah nilai yang paling banyak diulang dalam set data, yang paling kerap, kerana dalam pengedaran mungkin ada lebih dari satu fesyen.

Median

Semasa memesan set data, median adalah nilai pusat semuanya.

Langkah -langkah penyebaran

Mereka menunjukkan kebolehubahan data dan memberi gambaran sejauh mana atau tersebar mereka dari langkah -langkah pusat. Yang paling banyak digunakan ialah:

Julat

Ia adalah perbezaan antara nilai terbesar x_M dan x terkecil_m set data:

Julat = x_M - x_m

Varians

Mengukur sejauh mana data nilai purata. Untuk ini, purata dibuat, tetapi dengan perbezaan antara sebarang nilai x_Yo dan rata -rata, kuadrat untuk menghalang mereka daripada membatalkan satu sama lain. Biasanya dilambangkan oleh huruf Yunani σ kuadrat, atau dengan s²:

Sisihan piawai

Varians tidak mempunyai unit yang sama seperti data, jadi sisihan piawai ditakrifkan sebagai akar kuadrat varians dan dilambangkan sebagai σ atau s:

Pengagihan kekerapan

Daripada mengambil kira setiap data secara individu, lebih baik untuk mengelompokkannya dalam julat, yang memudahkan kerja, terutama jika terdapat banyak nilai. Sebagai contoh, ketika bekerja dengan anak -anak sekolah, mereka dapat dikelompokkan ke julat umur: dari 0 hingga 6 tahun, dari 6 hingga 12 tahun dan dari 12 hingga 18 tahun.

Graf

Mereka merupakan cara terbaik untuk menghargai pengedaran data pandangan, dan mengandungi semua maklumat yang dikumpulkan dalam jadual dan gambar, tetapi lebih berpatutan.

Terdapat pelbagai jenis mereka: dengan bar, linear, bulat, batang dan daun, histogram, poligon kekerapan dan pictograms. Contoh graf statistik dibentangkan dalam Rajah 3.

Tema minat

Cawangan statistik.

Pembolehubah statistik.

Penduduk dan sampel.

Statistik inferensi.

Rujukan

1. Faraldo, ms. Statistik dan metodologi penyelidikan. Pulih dari: EIO.USC.adalah.
2. Fernández, s. 2002. Statistik deskriptif. 2. Edisi. Editorial ESIC. Pulih dari: Buku Google.
3. Sejarah Statistik. Pulih dari: eumed.jaring.
4. Ibañez, ms. 2010. Matematik II. Pendekatan Kecekapan. Pembelajaran Cengage.
5. Monroy, s. 2008. Statistik deskriptif. 1st. Edisi. Institut Politeknik Kebangsaan Mexico.
6. Formula Universe. Statistik deskriptif. Pulih dari: universoformulas.com.