Faktor Biasa untuk Menggabungkan Istilah Contoh, Latihan

Dia Faktor Umum untuk Perjumpaan Syarat Ini adalah prosedur algebra yang membolehkan menulis beberapa ungkapan algebra dalam bentuk faktor. Untuk mencapai matlamat ini, ungkapan mesti terlebih dahulu mengumpulkan dan mengamati bahawa setiap kumpulan yang dibentuk telah, sebenarnya, faktor yang sama.

Memohon teknik dengan betul memerlukan beberapa amalan, tetapi dalam masa yang singkat, mungkin untuk menguasai. Mari kita lihat terlebih dahulu contoh ilustrasi yang diterangkan langkah demi langkah. Maka pembaca dapat menerapkan apa yang mereka pelajari dalam setiap latihan yang akan muncul setelah.

Rajah 1. Keluarkan faktor umum untuk mengumpulkan istilah memudahkan kerja dengan ekspresi algebra. Sumber: Pixabay.

Sebagai contoh, katakan anda perlu faktor ungkapan berikut:

2x² + 2xy - 3zx - 3zy

Ekspresi algebra ini terdiri daripada 4 monomial atau istilah, dipisahkan oleh tanda + dan -, iaitu:

2x², 2xy, -3zx, -3zy

Memerhatikan dengan teliti, x adalah biasa pada tiga yang pertama, tetapi tidak kepada yang terakhir, sementara dan biasa pada yang kedua dan keempat, dan z adalah biasa pada yang ketiga dan keempat.

Oleh itu, pada dasarnya tidak ada faktor yang sama dengan empat istilah pada masa yang sama, tetapi jika mereka dikelompokkan kerana ia akan dipaparkan di bahagian berikut, seseorang boleh membantu menulis ungkapan sebagai produk dua atau lebih faktor.

[TOC]

Contoh

Faktor ungkapan: 2x² + 2xy - 3zx - 3zy

Langkah 1: Kumpulan

2x² + 2xy - 3zx - 3zy = (2x² + 2xy) + (-3zx - 3zy)

Langkah 2: Keluarkan faktor biasa dari setiap kumpulan

2x² + 2xy - 3zx - 3zy =

= (2x² + 2xy) - (3zx + 3zy) =

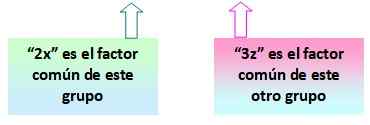
= 2x (x+y) - 3z (x+y)

YoMportante: Tanda negatif juga merupakan faktor biasa yang mesti diambil kira.

Boleh melayani anda: ruang vektor: asas dan dimensi, aksioma, sifat

Sekarang perhatikan bahawa kurungan (x+y) diulang dalam dua syarat yang diperoleh semasa kumpulan. Itulah faktor biasa yang dicari.

Langkah 3: Memastikan semua ungkapan

2x² + 2xy - 3zx - 3zy = (x+y) (2x - 3z)

Dengan hasil terdahulu, matlamat pemfaktoran telah dicapai, yang tidak lain adalah mengubah ungkapan algebra berdasarkan jumlah dan penolakan istilah, dalam produk dua atau lebih faktor, dalam contoh kami,: (x+ y) dan (2x - 3z).

Isu penting mengenai faktor kumpulan biasa

soalan 1: Bagaimana untuk mengetahui bahawa hasilnya betul?

Jawapan: Harta pengedaran digunakan untuk hasil yang diperoleh dan selepas mengurangkan dan memudahkan, ungkapan yang dicapai mesti bertepatan dengan yang asal, jika tidak, ada ralat.

Dalam contoh sebelumnya, ia berfungsi sebaliknya dengan hasilnya, untuk mengesahkan bahawa ia adalah baik:

(x+y) (2x - 3z) = 2x² -3zx +2xy - 3zy

Oleh kerana perintah tambahan tidak mengubah jumlahnya, setelah memohon harta pengedaran, semua istilah asal, ada tanda -tanda yang disertakan, oleh itu, pemfaktoran itu betul.

Soalan 2: Bolehkah anda berkumpul dengan cara lain?

Jawapan: Terdapat ungkapan algebra yang mengakui lebih daripada satu bentuk kumpulan dan lain -lain yang tidak. Dalam contoh yang dipilih, pembaca boleh mencuba kemungkinan lain, contohnya kumpulan:

2x² + 2xy - 3zx - 3zy = (2x²- 3zx) + (2xy - 3zy)

Dan anda dapat melihat bahawa hasilnya sama seperti yang diperolehi di sini. Mencari kumpulan yang optimum adalah soal amalan.

Boleh melayani anda: Cotangent Berasal: Pengiraan, Demonstrasi, Latihan

Soalan 3: Mengapa perlu mendapatkan faktor biasa dari ungkapan algebra?

Jawapan: Kerana terdapat aplikasi di mana ekspresi yang difikirkan memudahkan pengiraan. Contohnya, katakan anda mahu melakukan 2x² + 2xy - 3zx - 3zy sama dengan 0. Apa kemungkinannya?

Untuk menjawab kebimbangan ini, versi yang difikirkan jauh lebih berguna daripada perkembangan asal dari segi. Ia timbul seperti ini:

(x+y) (2x - 3z) = 0

Satu kemungkinan bahawa ungkapan itu bernilai 0 ialah x = -y, tanpa mengira nilai z. Dan yang lain ialah x = (3/2) z, tanpa masalah nilai y.

Latihan

- Latihan 1

Dapatkan faktor umum ungkapan berikut dengan mengumpulkan istilah:

kapak+ay+bx+oleh

Penyelesaian

Dua yang pertama dikelompokkan, dengan faktor umum "A" dan dua yang terakhir dengan faktor umum "B":

kapak+ay+bx+by = a (x+y)+b (x+y)

Sebaik sahaja ini dilakukan, faktor umum yang baru diturunkan, iaitu (x+y), supaya:

kapak+ay+bx+by = a (x+y)+b (x+y) = (x+y) (a+b)

Cara lain untuk berkumpulan

Ungkapan ini mengakui cara kumpulan lain. Mari kita lihat apa yang berlaku jika istilah disusun semula dan kumpulan dibuat dengan mana ia mengandungi x dan yang lain dengan yang mengandungi dan:

AX +AY +BX +BY = AX +BX +AY +BY = X (A +B) +Y (A +B)

Dengan cara ini faktor umum baru adalah (a+b):

AX+AY+BX+BY = AX+BX+AY+BY = X (A+B)+Y (A+B) = (X+Y) (A+B)

Yang membawa kepada hasil yang sama dari cara pertama kumpulan yang diuji.

- Latihan 2

Ia dikehendaki menulis ungkapan algebra berikut sebagai dua faktor produk:

Ke -3³ - Ke -3²B+9AB²-ke²+AB-3B²

Boleh melayani anda: mata coplanares: persamaan, contoh dan latihan yang diselesaikan

Penyelesaian

Ungkapan ini mengandungi 6 istilah. Mari cuba mengumpulkan pertama dan keempat, kedua dan ketiga dan akhirnya kelima dan keenam:

Ke -3³ - Ke -3²B+9AB²-ke²+AB-3B² = (3³ -ke²) + (- ke-3²B+9AB²) + (Ab-3b²)

Sekarang setiap kurungan adalah faktor:

= (3³ -ke²) + (- ke-3²B+9AB²) + (Ab -3b²) = a² (3a -1) + 3ab (3b -a) + b (a -3b)

Pada pandangan pertama nampaknya keadaan telah rumit, tetapi pembaca tidak boleh digalakkan, kerana kita akan menulis semula istilah terakhir:

ke² (3a -1) + 3ab (3b -a) + b (a -3b) = a² (3a - 1) + 3ab (3b -a) - b (3b -a)

Dua syarat terakhir kini mempunyai faktor yang sama, iaitu (3b-a), jadi mereka boleh difakkan. Sangat penting untuk tidak melupakan jangka masa pertama² (3a - 1), yang mesti terus menemani segala -galanya sebagai menambah, jadi anda tidak bekerja dengannya:

ke² (3a - 1) + 3ab (3b -a) - b (3b -a) = a² (3A-1) + (3B-A) (3AB-B)

Ekspresi telah dikurangkan kepada dua istilah dan faktor umum baru ditemui pada yang terakhir, iaitu "B". Sekarang ia tetap:

ke² (3a-1) + (3b-a) (3ab-b) = a² (3A-1) +B (3B-A) (3A-1)

Faktor umum seterusnya dalam muncul ialah 3 - 1:

ke² (3a - 1) +b (3b -a) (3a -1) = (3a - 1) [a² + B (3b-a)]

Atau jika anda lebih suka tanpa kurungan persegi:

(3 - 1) [a² + B (3b -a)] = (3a - 1) (a² -AB + 3B²)

Bolehkah pembaca mencari cara lain untuk mengumpulkan yang membawa kepada hasil yang sama?

Rajah 2. Latihan pemfaktoran yang dicadangkan. Sumber: f. Zapata.

Rujukan

1. Baldor, a. 1974. Algebra Elementary. Kebudayaan Venezuela s.Ke.
2. Jiménez, r. 2008. Algebra. Prentice Hall.
3. Kes utama pemfaktoran. Pulih dari: julioprofe.jaring.
4. Unam. Matematik Asas: Pemfaktoran dengan mengumpulkan istilah. Fakulti Perakaunan dan Pentadbiran.
5. Zill, d. 1984. Algebra dan trigonometri. Macgraw Hill.