Faktor pembungkusan

Faktor pembungkusan adalah pecahan yang menunjukkan berapa jumlah zarah yang diduduki, sama ada atom, ion atau molekul, di ruang dalaman kristal. Nilainya sentiasa kurang daripada 1, yang menjadi 100% daripada jumlah kaca; Lebih tepat lagi, sel kesatuannya, yang merupakan perwakilan terkecil dari seluruh kaca.

Faktor pembungkusan 100% bermaksud bahawa zarah menduduki jumlah sel kesatuan secara keseluruhan. Secara fizikal, mustahil untuk ini berlaku, kerana ia akan menyiratkan, sebagai contoh, atom -atom mengubah radio mereka dan membubarkan seolah -olah mereka adalah "cecair elektronik". Geometri atom, sfera untuk kemudahan, selalu menghasilkan ruang kosong semasa pembungkusan.

Seperti yang berlaku dalam mesin pengisaran yang manis, faktor pembungkusan memberitahu kita bagaimana "ketat" adalah zarah kristal: semakin besar, lebih banyak gusi, atau atom, akan ada ruang angkasa

Dalam definisi faktor pembungkusan, diandaikan bahawa atom terdiri daripada sfera tegar, seperti gusi atau bola gula -gula mesin yang dibebaskan (imej unggul). Di antara sfera akan sentiasa ada ruang kosong di mana sfera yang lebih kecil (kekotoran atau bahan tambahan dapat menyelinap).

Sekiranya kita meningkatkan faktor pembungkusan, sfera akan diperah, menjadikan kaca yang paling padat dan padat; atau sebaliknya, lebih cacat, seperti logam yang mudah dibentuk dan mulur.

Faktor pembungkusan digunakan untuk sebarang jenis kaca. Walau bagaimanapun, pengiraannya boleh menjadi sedikit membosankan, jadi ia hanya akan dipertimbangkan untuk kristal atom dengan struktur mudah.

[TOC]

Formula faktor pembungkusan

Faktor pembungkusan biasanya dinyatakan sebagai peratusan. Sebagai contoh, jika nilainya adalah 40%, ini bermakna zarah -zarah hampir tidak menduduki 40% daripada jumlah ruang sel unit; atau apa yang sama seperti menyatakan bahawa 60% kaca "kosong".

Di atas menjelaskan apakah formula untuk mengira faktor ini:

• Ugly = (Volume of Atoms)/ (Jilid Sel Unit)

Di mana cara hodoh Faktor Pembungkusan Atom, Apakah kristal paling mudah.

Jumlah sel unit bergantung kepada parameternya (seperti panjang sisinya), yang mana ia diteruskan oleh geometri mudah untuk mengira kelantangannya. Atom, sebaliknya, adalah mereka yang menentukan sel, jadi mungkin untuk menyatakan dimensi yang sama dari radio atom, seperti yang akan dilihat di bahagian seterusnya.

Ia boleh melayani anda: campuran racemik: chirtal, contoh

Berkenaan dengan jumlah atom, jumlahnya yang terdapat dalam sel unit (1, 2, 3, dan lain -lain.), serta geometri sfera. Oleh itu, formula diubah sedikit:

Ugly = (nº atom) (volum atom)/ (jumlah sel unit)

Untuk mengira hodoh, anda perlu menentukan kemudian, v_atom dan v_{Sel kesatuan}.

Cubic mudah

Sel unit padu mudah. Sumber: CCC_CRYSTAL_CELL_ (legap).SVG: *COBIQUE_CENTRE_ATOMES_PAR_MAILLE.SVG: Cdang (Idea Asal dan Pelaksanaan SVG), Samuel Dupré (3d Odeeling dengan Solidworks) Derve Work: Daniele Pugliesi (Talk) Derive Work: Daniele Pugliesi, CC By-SA 3.0, melalui Wikimedia Commons

Sel kesatuan yang paling mudah adalah kubik yang mudah. Di dalamnya kita mempunyai beberapa bahagian atom di setiap sudut. Sekiranya kita melihat, kita akan melihat bahawa panjangnya ke Dari sel ini sama dengan 2R, kerana ia adalah atom yang menentukan sel. Jadi, jumlah sel unit akan sama dengan:

V_{Sel kesatuan} = ke³ (jumlah kiub)

= (2r)³

= 8r³

Sementara itu, jumlah atom akan sama dengan:

V_atom = (4/3) πr³ (jumlah sfera)

Setiap sudut dikongsi oleh 8 lagi sel unit jiran. Oleh itu, kita mempunyai pecahan 1/8 di setiap sudut, dan mempunyai 8 daripadanya, kita tidak peduli 1 atom per unit sel (1/8 x 8 = 1).

Faktor pembungkusan adalah:

Ugly = (1) (4/3) πr³ /8r³

= π/6 ≈ 52%

Iaitu, dalam sel padu mudah atom menduduki 52% daripada keseluruhan jumlah kaca.

Padu berpusat di dalam badan

Penentuan kelantangan sel

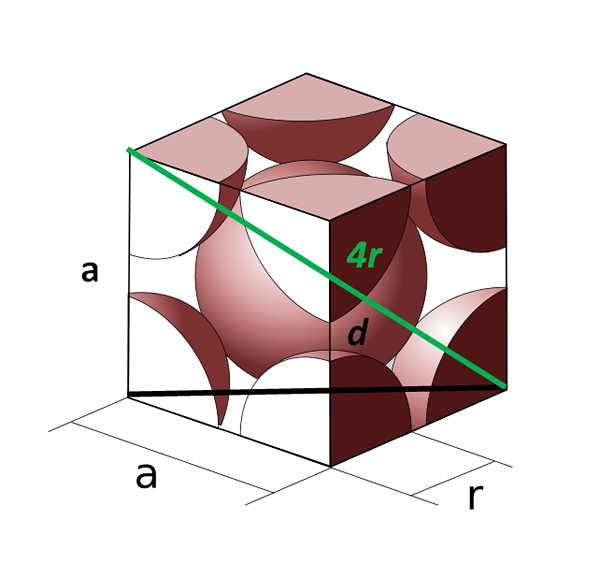Sel kesatuan badan berpusat pada badan. Sumber: COBIQUE_CENTRE_ATOMES_PAR_MAILLE.SVG: CDAG (Idea Asal dan Pelaksanaan SVG), Samuel Dupré (3D Odeeling dengan Solidworks) Kerja Derivatif: Daniele Pugliesi, CC BY-SA 3.0, melalui Wikimedia Commons

Sekarang mari kita lihat sel padu yang berpusat di badan. Sebelah ke Ia tidak lagi sama dengan 2r, kerana kita mempunyai ruang kosong antara kedua -dua atom sudut. Oleh itu, ada pepenjuru d sama dengan 4R (warna hijau) yang melintasi sel melalui pusat dan sentuh sudut yang bertentangan, dan satu lagi pepenjuru d muka (hitam).

Sisi ke, d dan 4R melukis segitiga segi empat tepat yang boleh kita gunakan trigonometri untuk mengira nilai ke:

(4r)² = d² + ke²

Boleh melayani anda: daya intermolecular

Tetapi sebaliknya, di dasar sel unit kita mempunyai segitiga lain (ke, ke dan d) yang mana kita boleh mengira hipotenus:

d²  = a² + ke²

= 2a²

Menggantikan maka kita akan mempunyai:

(4r)² = (2²) + a²

(4r)² = 3a²

A = (4/√3) r

V_{Sel kesatuan} adalah sama dengan:

V_{Sel kesatuan} = a³

= ((4/√3) r)³

Penentuan faktor pembungkusan

Perhatikan bahawa berkenaan dengan bilangan atom kita mempunyai 1 atom di dalam sel ini, berikutan potongan yang sama dibuat untuk sel padu mudah, dan atom tambahan lain yang terletak di tengah sel. Oleh itu, terdapat 2 atom untuk setiap sel padu yang berpusat pada badan.

Faktor pembungkusan kemudiannya:

Ugly = (2) (4/3) πr³ / ((4/ √3) r)³

= (√3/8) π ≈ 68%

Iaitu, dalam sel padu yang memberi tumpuan kepada badan, 68% daripada jumlah kaca diduduki oleh atom. Oleh itu, susunan kristal ini lebih padat (atau padat) daripada kubik yang mudah.

Padu berpusat di wajah

Penentuan kelantangan sel

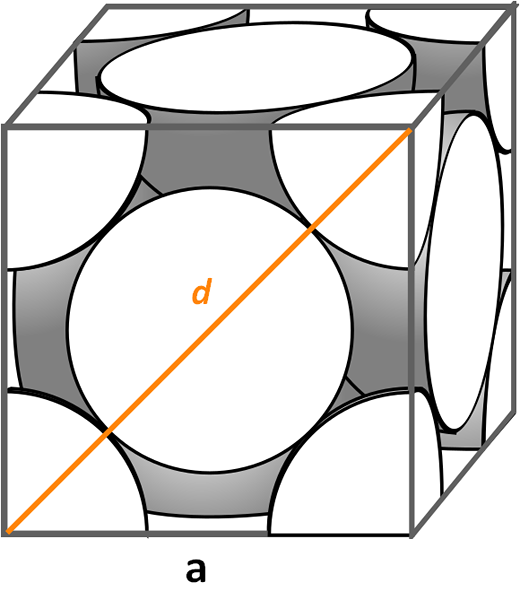Sel kesatuan kubik berpusat di wajah. Sumber: Cdang, CC By-SA 3.0, melalui Wikimedia Commons

Mari kita lihat sel kesatuan padu yang berpusat di wajah, sangat biasa dalam simfines garam bukan organik dan beberapa logam, seperti emas dan perak. Untuk menentukan faktor pembungkusannya, kita mesti memulakan, mengikuti contoh sebelumnya, untuk mencari berapa jumlah sel unitnya. Adalah perlu untuk mengira sisi lagi ke Dan sebagainya jumlah kiub ke³.

Kali ini prosedur lebih mudah dan lebih langsung, kerana kita mempunyai pepenjuru d Depan itu, bersama -sama dengan sisi ke, Mereka membentuk segitiga yang betul yang boleh kita gunakan trigonometri:

d² = a² + ke²

= 2a²

Penjelasan ke kita akan mempunyai:

ke = D/√2

Tetapi, kita perasan secara visual d Ia sama dengan 4R, jadi kami membuat penggantian:

ke = 4r/√2

= 2r 2^1-1/2

= (2√2) r

Menjadi v_{Sel kesatuan} sama dengan:

ke³ = ((2√2) r)³

= (16√2) r³

Mengenai bilangan atom setiap sel, kami mempunyai lapan bahagian satu atom di setiap sudut, dan juga separuh atom untuk setiap enam muka, yang dikongsi oleh sel lain yang berdekatan. Oleh itu, bilangan atom adalah sama dengan:

Atom nº = 1/8 (8) + 1/2 (6) = 1 + 3 = 4

Penentuan faktor pembungkusan

Memandangkan terdapat 4 atom di setiap sel padu yang memberi tumpuan kepada wajah, dan juga jumlahnya, yang sama dengan (16√2) r³, Kita kemudian boleh mengira faktor pembungkusan:

Ugly = (nº atom) (volum atom)/ (jumlah sel unit)

= (4) (4/3) πr³ / (16√2) r³

Ia boleh melayani anda: Kumpulan Acilo: Struktur, Ciri, Sebatian dan Derivatif

= π/(3√2) ≈ 74%

Perhatikan bahawa sel ini lebih padat daripada yang sebelumnya: 74% daripada jumlah keseluruhan sel diduduki oleh atom. Dalam kristal yang sempurna dan tulen, ini bersamaan dengan mengatakan bahawa 26% daripada jumlahnya tersedia untuk menjadi tuan rumah atom tetamu lain.

Hexagonal padat

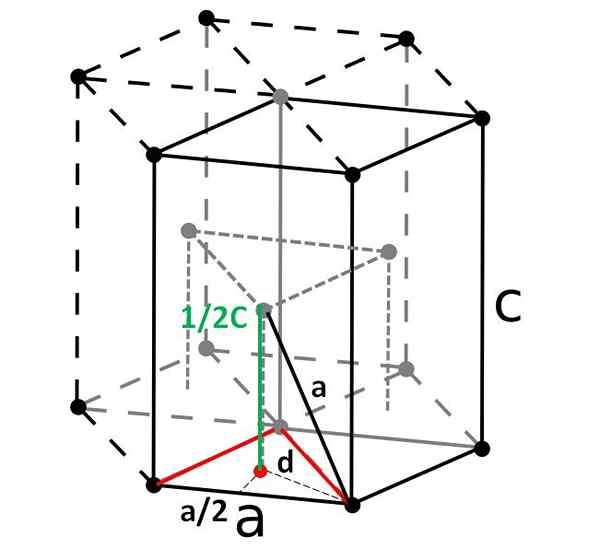Sel heksagon padat dan sel primitif rhombohedralnya. Sumber: Asal: Dornelfvector: Depiep, CC BY-SA 3.0, melalui Wikimedia Commons

Akhirnya, di antara sel unit yang paling mudah dan paling padat kita mempunyai heksagon padat. Tidak seperti yang sebelumnya, pengiraan jumlahnya sedikit lebih rumit. Seperti yang dapat dilihat, ia bukan padu, jadi ia mempunyai dua parameter ke dan c, Yang terakhir adalah ketinggian sel.

Penentuan ketinggian sel

Sel heksagon dapat dipecahkan kepada tiga sel rhomboyan, dan dari salah satu daripadanya ia akan dikira ke dan c. Sebelah ke, Walaupun tidak begitu jelas dalam imej di atas, ia sama dengan 2R. Untuk mengira c, Sebaliknya, kami menggunakan segitiga dan produk titik merah dari prisma segi tiga dalaman sel yang sama.

Kita perlu mengira jarak d Untuk dapat menentukan berapa harganya c. Di lantai segitiga merah adalah sama, dengan sudut 60º. Tetapi jika segitiga segi empat tepat dalaman lain dianggap dengan sisi ke/2 dan d, dan sudut 30º (separuh), kemudian dengan trigonometri kita dapat menentukan d:

Cos (30º) = (ke/2) / d

d = ke/√3

Dan sekarang kita menganggap segitiga yang betul terdiri daripada sisi c/2 (hijau), ke (hitam) dan d (bertitik):

ke² = (ke/√3)² + (C/2)²

Penjelasan c Kami akan mempunyai:

c = √ (8/3) ke

Dan menggantikan ke Oleh 2r:

c = √ (8/3) (2R)

= √ (4 · 2/3) (2R)

= 4√ (2/3) r

Penentuan kelantangan sel

Untuk menentukan kelantangan sel heksagon, anda perlu mengalikan kawasan heksagon dengan ketinggiannya. Mengetahui bahawa segitiga sama rata mempunyai sisi ke, ketinggiannya dikira h. Oleh itu, mencari kawasan segitiga, iaitu untuk kes ini √3/4ke², Kami membiak nilai ini dengan 6 untuk mendapatkan kawasan heksagon: 3 (√3/2)ke²

Oleh itu, jumlahnya:

V_{Sel kesatuan} = Ketinggian kawasan heksagon x

= 3 (√3/2)ke² X 4√ (2/3) r

Dan menggantikan sekali lagi ke Oleh 2r:

V_{Sel kesatuan}  = 3 (√3/2) (2R)² X 4√ (2/3) r

= 24√2 r³

Penentuan faktor pembungkusan

Di sel heksagon terdapat 12 atom di sudut, yang mempunyai 1/6 jumlahnya di dalamnya. Terdapat juga 3 atom dalaman yang jumlahnya selesai, dan 2 lagi atom di bahagian atas dan bawah yang separuh daripada jumlahnya berada di dalam sel.

Oleh itu, bilangan atom adalah sama dengan:

Nº atom = 1/6 (12) + 1 (3) + 1/2 (2) = 6 atom

Dan faktor pembungkusan akhirnya:

Ugly = (nº atom) (volum atom)/ (jumlah sel unit)

= (6) (4/3) πr³ / 24√2 r³

= π/(3√2) ≈ 74%

Perhatikan bahawa faktor petak untuk sel heksagon adalah sama seperti sel padu yang berpusat di wajah. Iaitu, kedua -duanya sama padat.

Rujukan

1. C. Barry Carter & m. Grant Norton. (2007). Sains dan Kejuruteraan Bahan Seramik. Springer.
2. Shiver & Atkins. (2008). Kimia bukan organik. (Edisi Keempat). MC Graw Hill.
3. Whitten, Davis, Peck & Stanley. (2008). Kimia. (8th ed.). Pembelajaran Cengage.
4. Wikipedia. (2021). Faktor Pembungkusan Atom. Diperoleh dari: dalam.Wikipedia.org
5. Brandon. (2021). Apakah faktor pembungkusan atom (dan bagaimana mengira ia untuk SC, BCC, FCC, dan HCP)? Pelajar Sains & Kejuruteraan Bahan. Pulih dari: msestudent.com