Formula kekerapan terkumpul, pengiraan, pengedaran, contoh

The kekerapan terkumpul Ia adalah jumlah frekuensi mutlak f, dari kanak -kanak yang sepadan dengan nilai tertentu pembolehubah. Sebaliknya, kekerapan mutlak adalah bilangan kali pemerhatian muncul dalam set data.

Jelas, pemboleh ubah kajian mesti teratur. Dan kerana kekerapan terkumpul diperoleh dengan menambahkan frekuensi mutlak, ternyata kekerapan terkumpul ke data terakhir mesti bertepatan dengan jumlahnya. Jika tidak ada ralat dalam pengiraan.

Kekerapan terkumpul digunakan dalam pengurusan data statistik

Secara umum, kekerapan terkumpul dilambangkan sebagai f_Yo (Atau kadang -kadang n_Yo), untuk membezakannya dari kekerapan mutlak f_Yo dan penting untuk menambah lajur untuknya di dalam jadual yang mana data dianjurkan, yang dikenali sebagai Jadual kekerapan.

Dengan cara ini ia difasilitasi, antara lain, untuk menyimpan akaun berapa banyak data yang dikira sehingga pemerhatian tertentu.

A f_Yo Ia juga dikenali sebagai Kekerapan terkumpul mutlak. Sekiranya anda membahagikan antara jumlah data, anda mempunyai Frekuensi terkumpul relatif, Jumlah akhir yang mesti sama dengan 1.

[TOC]

Formula

Kekerapan terkumpul nilai tertentu pembolehubah x_Yo  Ia adalah jumlah frekuensi mutlak f dari semua nilai yang lebih rendah daripada atau sama dengannya:

F_Yo  = f₁ + F₂ + F₃  +... f_Yo

Dengan menambahkan semua frekuensi mutlak, jumlah data n diperoleh, iaitu:

F₁ + F₂ + F₃ +… . + F_n = N

Operasi sebelumnya ditulis secara ringkas dengan simbol jumlah Σ:

Σ f_Yo = N

Frekuensi terkumpul lain

Frekuensi berikut juga boleh dikumpulkan:

-Frekuensi relatif: Ia diperoleh dengan membahagikan kekerapan mutlak f_Yo Antara jumlah data n:

F_r = f_Yo / N

Sekiranya frekuensi relatif ditambah dari kanak -kanak kepada yang sepadan dengan pemerhatian tertentu, kekerapan relatif terkumpul. Nilai terakhir mestilah sama dengan 1.

-Peratusan Kekerapan Terkumpul: Kekerapan relatif terkumpul setiap 100% didarab.

F_% = (f_Yo / N) x 100%

Frekuensi ini berguna untuk menggambarkan tingkah laku data, contohnya dengan mencari langkah kecenderungan pusat.

Cara mendapatkan kekerapan terkumpul?

Untuk mendapatkan kekerapan terkumpul, diperlukan untuk memerintahkan data dan menyusunnya dalam jadual kekerapan. Prosedur ini digambarkan dalam situasi praktikal berikut:

Boleh melayani anda: penggantian kompaun

-Di kedai dalam talian yang menjual telefon bimbit, rekod jualan jenama tertentu bulan Mac, nilai berikut setiap hari:

1; 2; 1; 3; 0; 1; 0; 2; 4; 2; 1; 0; 3; 3; 0; 1; 2; 4; 1; 2; 3; 2; 3; 1; 2; 4; 2; 1; 5; 5; 3

Pembolehubah adalah Bilangan telefon yang dijual sehari Dan ia kuantitatif. Data yang dibentangkan tidak begitu mudah untuk mentafsir, contohnya pemilik kedai mungkin berminat untuk mengetahui sama ada terdapat trend, seperti hari minggu ketika penjualan jenama itu lebih besar.

Maklumat seperti ini dan banyak lagi, ia dapat diperoleh dengan menyampaikan data dengan cara yang teratur dan menentukan frekuensi.

Cara Mengisi Jadual Kekerapan

Untuk mengira kekerapan terkumpul, data diperintahkan:

 0; 0; 0; 0; 1; 1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 2; 2; 2; 2; 3; 3; 3; 3; 3; 3; 4; 4; 4; 5; 5

Kemudian meja dengan maklumat berikut dibina:

-Lajur pertama di sebelah kiri dengan jumlah telefon yang dijual, antara 0 dan 5 dan dalam peningkatan urutan.

-Lajur kedua: kekerapan mutlak, iaitu bilangan hari yang dijual 0 telefon, 1 telefon, 2 telefon dan sebagainya.

-Lajur Ketiga: Kekerapan terkumpul, yang terdiri daripada jumlah kekerapan sebelumnya ditambah kekerapan data yang akan dipertimbangkan.

Lajur ini bermula dengan lajur pertama lajur frekuensi mutlak, dalam kes ini adalah 0. Untuk nilai seterusnya, ini ditambah dengan sebelumnya. Oleh itu, data terakhir kekerapan terkumpul diteruskan, yang mesti bertepatan dengan jumlah data.

Jadual kekebalan

Jadual berikut menunjukkan pemboleh ubah "bilangan telefon yang dijual dalam satu hari", kekerapan mutlaknya dan pengiraan terperinci kekerapannya yang terkumpul.

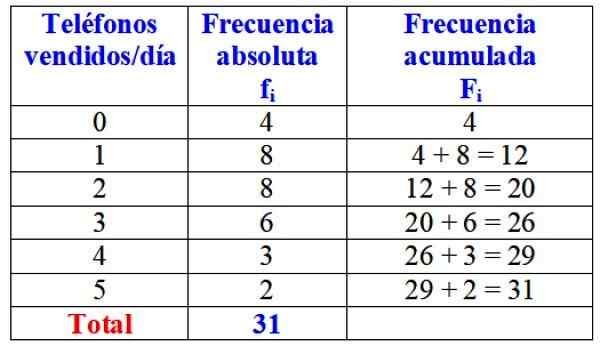Jadual frekuensi mutlak dan terkumpul untuk pemboleh ubah "Telefon yang dijual setiap hari". Sumber: f. Zapata.

Dalam pandangan pertama, boleh dikatakan bahawa jenama yang dimaksudkan hampir selalu dijual satu atau dua telefon sehari, kerana kekerapan yang paling mutlak adalah 8 hari, yang sepadan dengan nilai -nilai ini pembolehubah. Hanya selama 4 hari sebulan tidak menjual satu telefon.

Ia boleh melayani anda: Sebab Trigonometrik: Contoh, Latihan dan Aplikasi

Seperti yang dinyatakan, lebih mudah untuk memeriksa jadual daripada data longgar yang asalnya dikumpulkan.

Pengagihan kekerapan terkumpul

Pengagihan kekerapan terkumpul adalah jadual di mana frekuensi mutlak, frekuensi terkumpul, frekuensi relatif terkumpul dan frekuensi peratusan terkumpul tersedia.

Walaupun kelebihan mengatur data dalam jadual seperti yang sebelumnya diperhatikan, jika nombor data sangat besar, mungkin tidak cukup untuk mengaturnya seperti yang ditunjukkan di atas, kerana jika banyak frekuensi muncul, masih sukar untuk mentafsir.

Masalahnya boleh menjadi ubat dengan membina a Pengagihan kekerapan Oleh selang waktu, prosedur yang berguna apabila pemboleh ubah mengambil sejumlah besar nilai atau jika ia adalah pemboleh ubah berterusan.

Di sini nilai dikumpulkan ke dalam selang amplitud yang sama, yang dipanggil kelas. Kelas dicirikan dengan mempunyai:

-Had Kelas: adalah nilai melampau setiap selang, terdapat dua, had atas dan had yang lebih rendah. Secara umum, had atas tidak tergolong dalam selang waktu tetapi untuk berikut segera, sementara batas yang lebih rendah adalah milik.

-Jenama Kelas: Ia adalah titik tengah setiap selang, dan diambil sebagai nilai wakilnya.

-Lebar kelas: Ia dikira dengan menolak nilai utama dan terkecil (julat) dan membahagikan bilangan kelas:

Lebar kelas = julat / bilangan kelas

Maka penjelasan pengagihan kekerapan terperinci.

Contoh

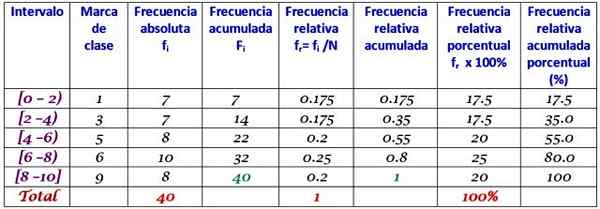
Set data ini sepadan dengan 40 gred peperiksaan matematik, pada skala dari 0 hingga 10:

0; 0; 0; 1; 1; 1; 1; 2; 2; 2; 3; 3; 3; 3; 4; 4; 4; 4; 5; 5; 5; 5; 6; 6; 6; 6; 7; 7; 7; 7; 7; 7; 8; 8; 8; 9; 9; 9; 10; 10.

Pengagihan kekerapan dengan jumlah kelas tertentu boleh dibangunkan, contohnya 5 kelas. Perlu diingat bahawa apabila menggunakan banyak kelas, data tidak mudah untuk mentafsir dan rasa melaksanakan kumpulan itu hilang.

Boleh melayani anda: Berapa banyak yang perlu anda tambahkan hingga 3/4 untuk mendapatkan 6/7?

Dan jika sebaliknya mereka dikelompokkan dengan sangat sedikit, maka maklumat itu dicairkan dan sebahagian daripadanya hilang. Semuanya bergantung pada jumlah data yang anda ada.

Dalam contoh ini adalah idea yang baik untuk mempunyai dua skor dalam setiap selang, kerana terdapat 10 skor dan 5 kelas akan dibuat. Peringkat adalah penolakan antara penarafan utama dan terkecil, lebar kelas menjadi:

Lebar kelas = (10-0)/5 = 2

Selang ditutup oleh kiri dan terbuka di sebelah kanan (kecuali yang terakhir), yang dilambangkan dengan kurungan persegi dan kurungan masing -masing. Semua mempunyai lebar yang sama, tetapi tidak wajib walaupun yang paling kerap.

Setiap selang mengandungi sejumlah elemen atau kekerapan mutlak, dan dalam lajur berikut adalah kekerapan terkumpul, di mana jumlahnya dibawa. Jadual juga menunjukkan kekerapan relatif f_r  (Kekerapan mutlak antara jumlah data) dan peratusan peratusan peratusan f f_r × 100%.

Latihan yang dicadangkan

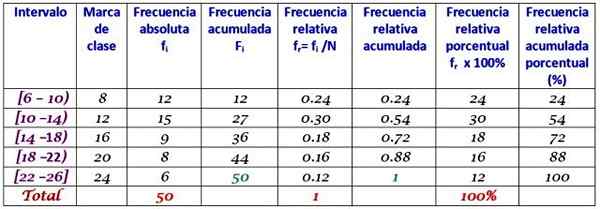
Sebuah syarikat membuat panggilan harian kepada pelanggannya selama dua bulan pertama tahun ini. Data adalah seperti berikut:

6, 12, 7, 15, 13, 18, 20, 25, 12, 10, 8, 13, 15, 6, 9, 20, 24, 12, 7, 10, 11, 13, 9, 12, 15, 18, 20, 13, 17, 23, 25, 14, 18, 6, 14, 16, 9, 6, 10, 12, 13, 17, 14, 26, 7, 12, 24, 7, 7, 7, 7,

Kumpulan dalam 5 kelas dan membina jadual dengan pengagihan kekerapan.

Jawapan

Lebar kelas adalah:

(26-6)/5 = 4

Cuba selesaikannya sebelum melihat jawapannya.

Rujukan

1. Berenson, m. 1985. Statistik untuk Pentadbiran dan Ekonomi. Inter -American s.Ke.
2. DEVORE, J. 2012. Kebarangkalian dan statistik untuk kejuruteraan dan sains. Ke -8. Edisi. Cengage.
3. Levin, r. 1988. Statistik untuk pentadbir. 2. Edisi. Prentice Hall.
4. Kebarangkalian dan statistik. Lebar selang kelas. Diperolehi daripada: Pedroprobabability dan stadistik.Blogspot.com.
5. Spiegel, m. 2009. Statistik. Siri Schaum. 4 ta. Edisi. McGraw Hill.
6. Walpole, r. 2007. Kebarangkalian dan statistik untuk kejuruteraan dan sains. Pearson.