Formula kekerapan mutlak, pengiraan, pengedaran, contoh

The Frekuensi mutlak Ditakrifkan sebagai bilangan kali data yang sama diulangi dalam set pemerhatian pemboleh ubah berangka. Jumlah frekuensi mutlak bersamaan dengan jumlah data.

Apabila terdapat banyak nilai pemboleh ubah statistik, mudah untuk mengaturnya dengan betul untuk mengekstrak maklumat mengenai tingkah laku mereka. Maklumat sedemikian diberikan oleh langkah kecenderungan pusat dan langkah penyebaran.

Rajah 1. Kekerapan mutlak pemerhatian statistik adalah kunci untuk mencari trend yang mengikuti set data

Dalam pengiraan langkah -langkah ini, data diwakili melalui kekerapan yang mana ia muncul dalam semua pemerhatian.

Contoh berikut menunjukkan bagaimana mendedahkan kekerapan mutlak setiap data adalah. Pada separuh pertama bulan Mei, ini adalah saiz kostum koktel yang terbaik, dari gudang pakaian wanita yang terkenal:

8; 10; 8; 4; 6; 10; 12; 14; 12; 16; 8; 10; 10; 12; 6; 6; 4; 8; 12; 12; 14; 16; 18; 12; 14; 6; 4; 10; 10; 18

Berapa banyak pakaian yang dijual dalam saiz tertentu, contohnya saiz 10? Pemilik berminat untuk mengetahui pesanan.

Memesan data lebih mudah dikira, terdapat 30 pemerhatian secara keseluruhan, daripada yang diperintahkan dari yang terkecil hingga yang tertinggi adalah seperti ini:

4; 4; 4; 6; 6; 6; 6; 8; 8; 8; 8; 10; 10; 10; 10; 10; 10; 12; 12; 12; 12; 12; 12; 14; 14; 14; 16; 16; 18; 18

Dan sekarang jelas bahawa saiz 10 diulang 6 kali, oleh itu kekerapan mutlaknya sama dengan 6. Prosedur yang sama dijalankan untuk mengetahui kekerapan mutlak saiz yang tinggal.

[TOC]

Formula

Kekerapan mutlak, dilambangkan sebagai f_Yo, Ia sama dengan bilangan kali sebagai nilai x tertentu_Yo berada dalam kumpulan pemerhatian.

Dengan mengandaikan bahawa jumlah pemerhatian adalah nilai n, jumlah semua frekuensi mutlak mestilah sama dengan nombor tersebut:

Boleh melayani anda: papomudas

Σf_Yo = f₁ + F₂ + F₃ +... f_n = N

Frekuensi lain

Sekiranya setiap nilai f_Yo Ia dibahagikan dengan jumlah data n, anda mempunyai frekuensi relatif F_r nilai x_Yo:

F_r = f_Yo / N

Frekuensi relatif adalah nilai antara 0 dan 1, kerana n sentiasa lebih besar daripada f_Yo, Tetapi jumlahnya mestilah sama dengan 1.

Mengalikan dengan 100 hingga setiap nilai f_r anda mempunyai Frekuensi peratusan relatif, Jumlahnya 100%:

Frekuensi peratusan relatif = (f_Yo / N) x 100%

Ia juga penting kekerapan terkumpul F_Yo Sehingga pemerhatian tertentu, ini adalah jumlah semua frekuensi mutlak sehingga kata pemerhatian termasuk:

F_Yo = f₁ + F₂ + F₃ +... f_Yo

Sekiranya kekerapan terkumpul dibahagikan dengan jumlah data n, anda mempunyai kekerapan relatif terkumpul, yang berlipat ganda setiap 100 hasil di Peratusan Frekuensi Relatif Terkumpul.

Cara mendapatkan kekerapan mutlak?

Untuk mencari kekerapan mutlak nilai tertentu yang dimiliki oleh set data, semuanya dianjurkan dari yang paling sedikit ke yang paling besar dan nilai dikira.

Dalam contoh saiz pakaian, kekerapan mutlak saiz 4 adalah 3 pakaian, iaitu f₁ = 3. Untuk saiz 6, 4 pakaian telah dijual: f₂ = 4. Dalam saiz 8 4 pakaian juga dijual, f₃ = 4 dan sebagainya.

Tabulasi

Jumlah hasil boleh diwakili dalam jadual yang menunjukkan frekuensi mutlak masing -masing:

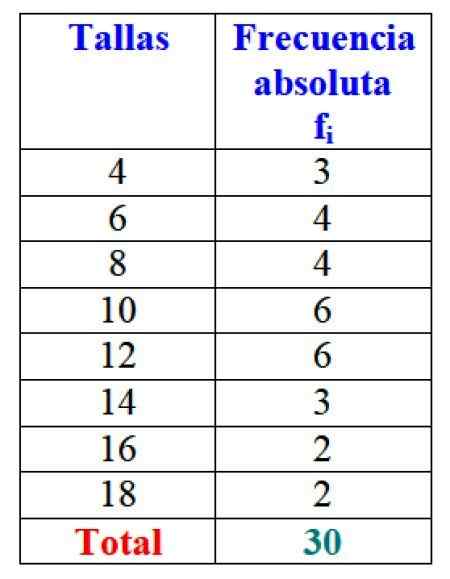Rajah 2. Jadual yang mewakili pembolehubah "Jualan Jualan" dan frekuensi mutlak masing -masing. Sumber: f. Zapata.

Jelasnya adalah berfaedah untuk memerintahkan maklumat dan dapat mengaksesnya, bukannya bekerja dengan data longgar.

Penting: Perhatikan bahawa dengan menambahkan semua nilai lajur f_Yo  Jumlah data selalu diperoleh. Sekiranya tidak, perakaunan mesti dikaji semula, kerana terdapat ralat.

Jadual kekerapan lanjutan

Jadual sebelumnya boleh dilanjutkan dengan menambahkan jenis kekerapan lain dalam lajur berturut -turut ke kanan:

Boleh melayani anda: homocedasticity: apakah, kepentingan dan contoh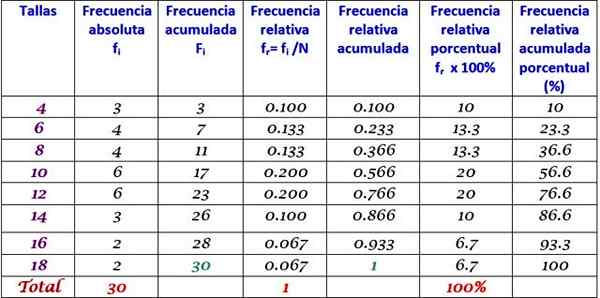

Pengagihan kekerapan

Pengagihan kekerapan adalah hasil penganjuran data dari segi frekuensi mereka. Apabila bekerja dengan banyak data, mudah untuk mengumpulkannya ke dalam kategori, selang atau kelas, masing -masing dengan frekuensi masing -masing: mutlak, relatif, terkumpul dan peratusan.

Objektif untuk melakukannya adalah dengan lebih mudah mengakses maklumat yang dimiliki oleh data, serta menafsirkannya dengan betul, yang tidak mungkin apabila mereka dibentangkan tanpa perintah.

Dalam contoh saiz, data tidak dikumpulkan, kerana mereka tidak terlalu banyak saiz dan mudah dimanipulasi dan dikira. Pembolehubah kualitatif juga boleh dilakukan dengan cara ini, tetapi apabila data sangat banyak, mereka bekerja lebih baik mengumpulkannya dalam kelas.

Pengagihan kekerapan untuk data dikumpulkan

Untuk mengumpulkan data dalam kelas yang sama saiz, yang berikut mesti dipertimbangkan:

-Saiz, lebar atau amplitud kelas: Ia adalah perbezaan antara nilai terbesar kelas dan minor.

Saiz kelas diputuskan dengan membahagikan julat r dengan bilangan kelas untuk dipertimbangkan. Julat adalah perbezaan antara nilai maksimum data dan kanak -kanak, seperti ini:

Saiz kelas = julat / bilangan kelas.

-Had Kelas: selang yang pergi dari had bawah ke had atas kelas.

-Jenama Kelas: Ia adalah titik tengah selang, yang dianggap wakil kelas. Ia dikira dengan separuh hayat atas dan had bawah kelas.

-Bilangan kelas: Formula Sturges boleh digunakan:

Kelas = 1 + 3,322 log n

Di mana n adalah bilangan kelas. Seperti biasanya nombor perpuluhan, berikut adalah bulat.

Contoh

Mesin kilang besar tidak beroperasi, kerana ia mengalami kegagalan berulang. Tempoh tidak aktif berturut -turut dalam beberapa minit, mesin tersebut, direkodkan di bawah, dengan sejumlah 100 data:

Ia boleh melayani anda: kebarangkalian kekerapan: konsep, bagaimana ia dikira dan contohnya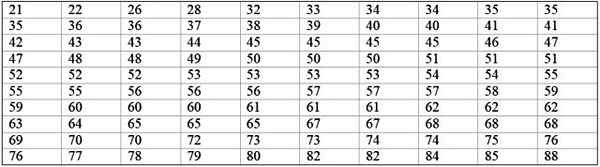

Pertama bilangan kelas ditentukan:

Kelas = 1 + 3,322 log n = 1 + 3.32 log 100 = 7.64 ≈ 8

Saiz kelas = julat / bilangan kelas = (88-21) / 8 = 8.375

Ia juga merupakan nombor perpuluhan, jadi ia memerlukan 9 sebagai saiz kelas.

Jenama kelas adalah purata antara had kelas atas dan bawah, contohnya untuk kelas [20-29) terdapat tanda:

Jenama kelas = (29 + 20) / 2 = 24.5

Teruskan dengan cara yang sama untuk mencari jenama kelas selang selang.

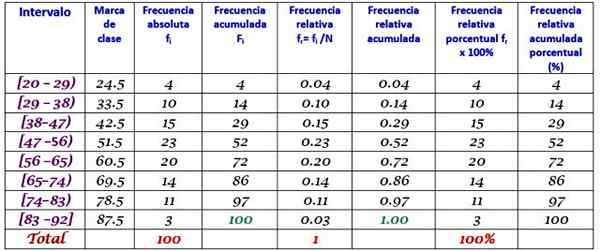
Latihan diselesaikan

40 orang muda menunjukkan bahawa masa dalam beberapa minit yang berlalu di internet pada Ahad lepas adalah yang akan datang, diperintahkan semakin:

0; 12; dua puluh; 35; 35; 38; 40; Empat lima; 45, 45; 59; 55; 58; 65; 65; 70; 72; 90; 95; 100; 100; 110; 110; 110; 120; 125; 125; 130; 130; 130; 150; 160; 170; 175; 180; 185; 190; 195; 200; 220.

Diminta untuk membina pengagihan kekerapan data ini.

Penyelesaian

Kedudukan r dari set n = 40 data adalah:

R = 220 - 0 = 220

Permohonan formula Sturges untuk menentukan bilangan kelas menghasilkan hasil berikut:

Kelas = 1 + 3,322 log n = 1 + 3.32 log 40 = 6.3

Seperti perpuluhan, keseluruhannya adalah 7, oleh itu data dikelompokkan menjadi 7 kelas. Setiap kelas mempunyai lebar:

Saiz kelas = julat / bilangan kelas = 220/7 = 31.4

Nilai dekat dan bulat ialah 35, oleh itu lebar kelas 35 dipilih.

Tanda kelas dikira dengan purata had atas dan bawah setiap selang, contohnya, untuk selang [0.35):

Jenama kelas = (0+35)/2 = 17.5

Kami meneruskan dengan cara yang sama dengan kelas yang tinggal.

Akhirnya, frekuensi dikira mengikut prosedur yang diterangkan di atas, mengakibatkan pengedaran berikut:

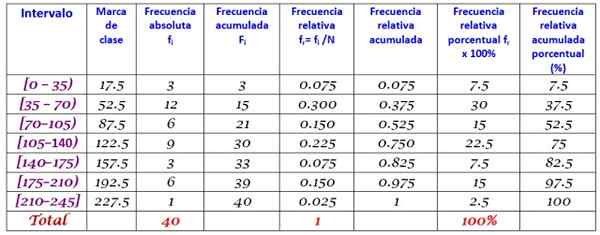
Rujukan

1. Berenson, m. 1985. Statistik untuk Pentadbiran dan Ekonomi. Inter -American s.Ke.
2. DEVORE, J. 2012. Kebarangkalian dan statistik untuk kejuruteraan dan sains. Ke -8. Edisi. Cengage.
3. Levin, r. 1988. Statistik untuk pentadbir. 2. Edisi. Prentice Hall.
4. Spiegel, m. 2009. Statistik. Siri Schaum. 4 ta. Edisi. McGraw Hill.
5. Walpole, r. 2007. Kebarangkalian dan statistik untuk kejuruteraan dan sains. Pearson.