Fungsi Berkembang Cara Mengenalpasti, Contoh, Latihan

Awak ada satu fungsi berkembang Apabila nilai y meningkat jika x juga meningkat, berbanding dengan fungsi penurunan, di mana nilai dan berkurangan apabila x meningkat.

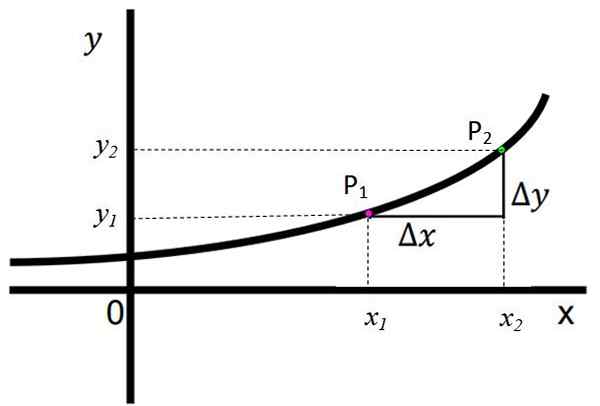
Angka berikut menunjukkan fungsi yang semakin meningkat, dan jelas diperhatikan bahawa apabila bergerak dari kiri ke kanan pada paksi x, nilai koordinat masing -masing dan, bersamaan dengan f (x), secara beransur -ansur meningkat. Dikatakan bahawa jika untuk semuanya x₂ > x₁, Kemudian ia wujud dan₂ > dan₁.

Rajah 1. Fungsi yang semakin meningkat. Sumber: f. Zapata.

Mata p₁ Dan p₂ Mereka ditunjukkan, masing -masing, koordinat (x₁, dan₁) dan (x₂,dan₂). Mereka ditakrifkan:

Δy = y₂ -dan₁

Δx = x₂ -x₁

Dalam fungsi ini, kedua -dua Δy dan Δx mempunyai tanda positif, yang bermaksud dan₂ > dan₁ dan x₂ > x₁, masing -masing. Ini adalah tanda yang jelas bahawa fungsi itu berkembang dengan berkesan.

Contoh yang baik dari fungsi yang sentiasa berkembang (meningkatkan membosankan) adalah logaritma neperian nombor sebenar. Semakin tinggi bilangannya, semakin besar logaritmanya.

[TOC]

Cara mengenal pasti fungsi yang semakin meningkat?

Dalam fungsi yang mudah dan berterusan seperti yang ditunjukkan dalam Rajah 1, mudah untuk menentukan sama ada fungsi semakin meningkat atau berkurang, dengan syarat grafik ada.

Walau bagaimanapun, fungsi yang lebih kompleks dapat tumbuh dalam beberapa selang dan penurunan pada orang lain. Itulah sebabnya kita bercakap Selang pertumbuhan dan penurunan fungsi.

Di rangkaian terdapat grafik dalam talian percuma, seperti geogebra, yang membolehkan grafik semua jenis fungsi. Memiliki graf, mudah untuk menentukan sama ada fungsi sentiasa meningkat, seperti f (x) = log x atau jika ia mempunyai selang di mana ia tumbuh dan yang lain di mana ia berkurangan dan apa itu.

Kriteria derivatif pertama

Memandangkan selang berangka tertentu i, jika kuantiti antara kuantiti Δy dan Δx positif, fungsi semakin meningkat. Dan sebaliknya, jika negatif, fungsi itu berkurangan.

Ia boleh melayani anda: kebarangkalian kekerapan: konsep, bagaimana ia dikira dan contohnya

Kamu perlu:

Δy / Δx> 0 → fungsi berkembang

Hakikat bahawa Δy / Δx> 0 dan fungsi semakin meningkat dalam selang tertentu, menunjukkan bahawa yang pertama diperoleh dari fungsi, atau sebaliknya tandanya, boleh digunakan sebagai kriteria untuk menentukan sama ada, fungsi tumbuh secara tertentu selang atau bahkan di titik tertentu domain anda.

Malah, derivatif pertama ditakrifkan sebagai cerun lengkung setiap titik:

Yang bermaksud bahawa Δx dapat dilakukan sekecil yang anda mahukan. Jika f '(x)> 0 untuk nilai tertentu x, contohnya x = a, cerun lengkung pada titik f' (a) positif dan fungsi akan meningkat di sana.

Teorem berikut menawarkan kriteria untuk mengetahui apabila fungsi berkembang dalam selang (a, b):

Teorem

Biarkan f (x) menjadi fungsi terbitan dalam (a, b). Jika f '(x)> 0, untuk apa -apa nilai x milik selang tersebut, dikatakan bahawa f (x) berkembang dalam (a, b).

Teorem ini digunakan untuk mengetahui di mana selang fungsi tumbuh, berikutan langkah -langkah ini:

Langkah 1

Cari mata di mana f '(x) = 0, dan juga yang f' (x) tidak wujud. Ini, dipanggil mata kritikal, Ini adalah titik di mana f '(x) boleh menukar tanda dan oleh itu f (x) mempunyai peluang untuk bergerak dari berkembang ke penurunan atau sebaliknya.

Langkah 2

Cari tanda f '(x) untuk nilai sewenang -wenangnya dalam setiap selang yang ditentukan oleh titik yang terdapat dalam langkah 1.

Langkah 3

Gunakan teorem untuk mengetahui sama ada fungsi semakin meningkat atau tidak dalam setiap selang waktu.

Contoh fungsi yang semakin meningkat

Terdapat fungsi yang mempunyai selang pertumbuhan dan yang lain penurunan, tetapi yang ditunjukkan di bawah selalu berkembang.

Berat berdasarkan umur

Berat orang sejak dilahirkan, sehingga kira -kira menamatkan remaja, hampir selalu menjadi fungsi usia yang semakin meningkat. Bayi dan kanak -kanak berkembang dan berkembang selama bertahun -tahun, dan kemudian, apabila mereka mencapai dewasa, sepanjang hayat mereka dijangka mengekalkan berat badan yang stabil, walaupun naik dan turun sangat kerap.

Boleh melayani anda: garis menegak

Fungsi logaritma

Fungsi logaritma pembolehubah sebenar neperian f (x) = ln x dan logaritma perpuluhan f (x) = log x selalu tumbuh.

Fungsi akar kuadrat nombor sebenar

Fungsi lain yang sentiasa berkembang ialah fungsi akar kuadrat nombor sebenar yang positif:

y = √x

Fungsi yang berkaitan dan fungsi linear

Fungsi yang berkaitan:

f (x) = mx + b

Ia berkembang apabila garis adalah cerun positif. Begitu juga, identiti dan fungsi linear:

f (x) = x dan f (x) = kapak, dengan> 0

Mereka tumbuh di semua domain mereka.

Fungsi eksponen

Fungsi eksponen seperti f (x) = e^x  Dan secara umum, fungsi bentuk:

f (x) = a^x, Dengan> 1

Mereka tumbuh di semua domain mereka.

Fungsi indeks impar yang berpotensi

Fungsi berpotensi eksponen ganjil, seperti ini:

• f (x) = x³
• g (x) = x⁵

Mereka selalu tumbuh.

Latihan

Latihan 1

Tentukan di mana selang fungsi yang diwakili dalam graf berikut semakin meningkat:

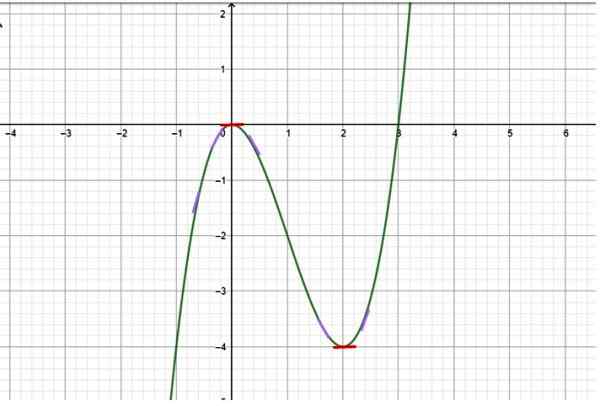Rajah 2. Berfungsi dengan pertumbuhan dan penurunan selang waktu. Sumber: f. Zapata.

Penyelesaian

Oleh kerana grafik tersedia, dari pemerhatian yang teliti ia ditentukan bahawa fungsi itu mempunyai tingkah laku berikut:

-Dari x → -∞ hingga x = 0 fungsi semakin meningkat, kerana nilai y menjadi kurang dan kurang negatif. Segmen cerun kecil telah ditarik dalam ungu untuk menunjukkan cerun garis tangen ke lengkung pada pelbagai titik (cerun tangen ke lengkung adalah tepat derivatif pertama).

Segmen -segmen ini mempunyai cerun positif, jadi teorem memastikan bahawa fungsi berkembang dalam selang ini.

-Tetapi pada x = 0 cerun lengkung dibatalkan, yang ditunjukkan dengan segmen merah mendatar kecil. Ini adalah Titik kritikal fungsi.

Boleh melayani anda: Apakah matematik dan apa yang mereka buat? 7 aplikasi penting

Dari situ fungsi mula berkurang, menjadi lebih negatif nilai dan. Keadaan ini berterusan sehingga x = 2, yang merupakan titik kritikal yang lain.

Kemudian, dalam selang dari x = 0 hingga x = 2 fungsi berkurangan.

-Dari x = 2 fungsi menjadi kurang dan kurang negatif, sehingga pada x = 3 melintasi paksi x dan terus menjadi lebih positif setiap kali. Oleh itu ini adalah selang pertumbuhan.

Kesimpulan: Selang pertumbuhan adalah (--∞, 0) dan (2, ∞+), sementara selang penurunan adalah (0.2).

Latihan 2

Tentukan selang pertumbuhan fungsi berikut, melalui kriteria derivatif pertama:

f (x) = x² - 2x

Penyelesaian

Berikutan langkah -langkah yang ditunjukkan di atas, derivatif pertama dikira dan sama dengan 0 untuk mencari titik kritikal:

f '(x) = 2x -2

2x - 2 = 0

x = 1

Nilai ini menentukan kewujudan selang (-∞, 1) dan (1, ∞+). Dua nilai sewenang -wenang dipilih yang dimiliki oleh masing -masing:

-Untuk x = 0, yang dimiliki oleh (-∞, 1), anda perlu f '(0) = 2.0 - 2 = -2. Hasilnya negatif, fungsi berkurangan dalam selang ini.

-Untuk x = 3, milik (1, ∞+), derivatif pertama bernilai f '(3) = 2.3 - 2 = 4. Oleh kerana hasilnya positif, disimpulkan bahawa fungsi tumbuh dalam selang ini.

Pembaca boleh grafik fungsi asal f (x) = x² - 2x pada grafik dalam talian untuk menyokong hasil ini.

Rujukan

1. Ayres, f. 2000. Pengiraan. 5ed. MC Graw Hill.
2. Leithold, l. 1992. Pengiraan dengan geometri analisis. Harla, s.Ke.
3. Purcell, e. J., Varberg, d., & Rigdon, s. Dan. (2007). Pengiraan. Mexico: Pendidikan Pearson.
4. Matemobile. Fungsi, berkembang, berkurangan dan tetap. Pulih dari: Matemovil.com
5. Requena, b. Fungsi yang semakin meningkat. Pulih dari: universoformulas.com.
6. Stewart, J. 2006. Preccculment: Matematik untuk Pengiraan. 5th. Edisi. Pembelajaran Cengage.