Ciri -ciri fungsi, contoh, latihan terhenti

The fungsi terhuyung -huyung y = s (x) adalah fungsi yang ditakrifkan dalam kepingan atau oleh bahagian -bahagian, sehingga dalam selang terhingga [a, b] ia mempunyai bilangan ketidakselarasan yang terhingga, yang akan kita panggil x₀ < x₁ < x₂ <… . x_n.  Dalam setiap selang terbuka (x_Yo , x_i+1), dan mempunyai nilai malar nilai s_Yo, Dengan ketidakpatuhan -saltos- pada titik x_Yo.

Graf yang dihasilkan dari fungsi seperti ini terdiri daripada langkah atau langkah. Mari lihat contoh di bawah:

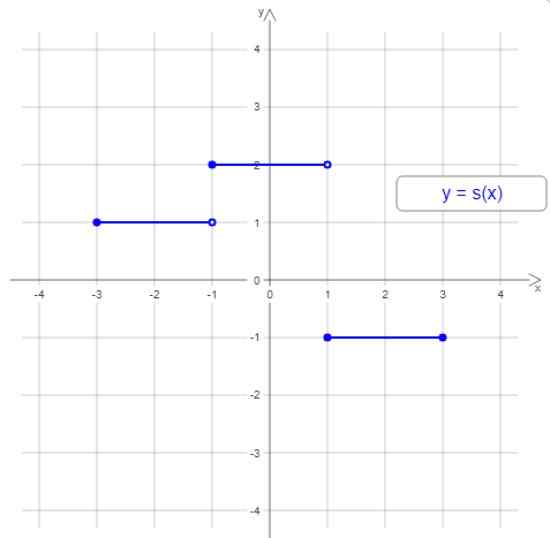
Rajah 1. Contoh fungsi terhuyung. Sumber: Wikimedia Commons.

Grafik fungsi melangkah ini mempunyai tiga langkah atau selang waktu yang terhuyung. Lebar langkah boleh berbeza dan tangga tidak selalu naik atau turun.

Fungsi contoh contohnya boleh ditulis dengan menentukan lebar dan tinggi setiap langkah, seperti ini:

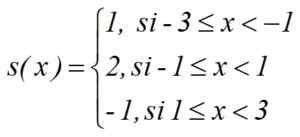
[TOC]

Ciri -ciri fungsi melangkah

-Fungsi ini menerima namanya dengan graf dalam bentuk langkah -langkah, yang diberikan oleh segmen yang mengarangnya. Setiap segmen mempunyai sebahagian daripada domain fungsi dan dalam setiap satu, fungsinya adalah malar.

-Domain fungsi berperingkat adalah nilai -nilai yang dimiliki oleh selang waktu yang ditakrifkan: [a, b], sementara julatnya dibentuk oleh nilai s_Yo ketinggian langkah.

Dalam contoh Rajah 1, domain adalah selang [-3,3] dan julatnya ialah nilai -1, 1 dan 2.

-Fungsi terhuyungnya berterusan kecuali dalam nilai -nilai yang membatalkan setiap langkah, titik x_Yo.

-Fungsi Escalonada dapat ditambah dan didarabkan untuk menimbulkan fungsi baru yang melangkah.

-Derivatifnya adalah 0 untuk titik -titik di mana ia ditakrifkan, kerana di dalamnya fungsi itu tetap. Bagi pihaknya, derivatif tidak wujud dalam ketidakpastian.

-Integral fungsi melangkah s (x) antara ke dan b Ia wujud dan sepadan dengan jumlah kawasan segi empat tepat lebar x_Yo- x_I-1 dan ketinggian s_k, sama dengan langkah.

Boleh melayani anda: peristiwa bebas: demonstrasi, contoh, latihan

Oleh kerana kawasan segi empat tepat adalah produk asas dengan ketinggian, kita perlu:

Contoh fungsi terhuyung -huyung

Di dalam fungsi yang terhuyung -huyung terdapat beberapa jenis, contohnya fungsi seluruh bahagian dan fungsi Langkah kesatuan, Serta pelbagai fungsi berperingkat yang menggambarkan situasi yang sama, seperti kadar banyak perkhidmatan. Mari lihat beberapa contoh:

- Contoh 1: Seluruh pihak

Fungsi keseluruhan bahagian sering menggunakan pendakap berganda:

f (x) = [[x]]

Dan ia ditakrifkan sebagai fungsi yang diberikan kepada setiap nombor sebenar integer yang terdekat atau lebih kecil, mengabaikan perpuluhan yang mempunyai nombor. Seperti yang berlaku, kita ada:

Fungsi bumbung atau langit

Menyerahkan kepada setiap domain nilai integer terdekat dengan kelebihan. Sebagai contoh:

[[+2.56]] = 3

Bahagian perpuluhan yang 0 diabaikan.56 dan integer terdekat diberikan yang lebih besar daripada 2.

Contoh yang lain:

[[-4.2]]= -3

Sekali lagi bahagian perpuluhan 0 ditinggalkan.2 dan integer tertinggi yang paling dekat dengan -4 diambil sebagai nilai fungsi, iaitu -3.

Dalam angka berikut adalah graf fungsi siling, ambil perhatian bahawa langkah itu dibatasi oleh bulatan berongga kecil ke kiri dan satu penuh ke kanan, kerana beberapa selang waktu, integer terbesar diberikan antara hujung antara di antara hujung antara berakhir di antara hujung selang waktu.

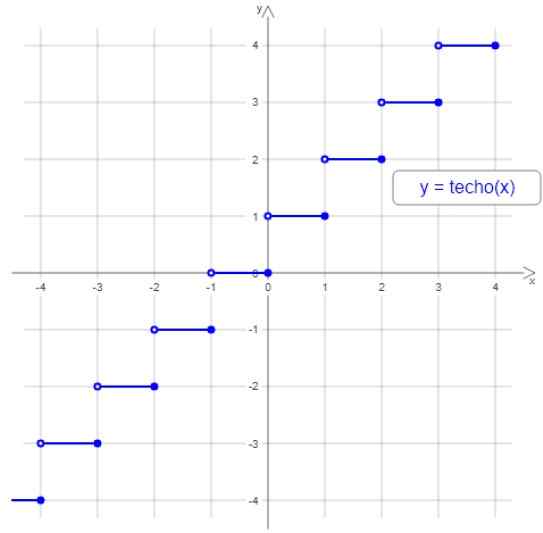Rajah 2. Fungsi bumbung atau langit. Sumber: Wikimedia Commons.

Sebagai contoh, semua nilai antara 3 dan 4 diberikan keseluruhan 4, yang antara -2 dan -1 diberikan -1 dan sebagainya.

Fungsi lantai atau tanah

Diberikan kepada setiap nilai domain nombor keseluruhan yang paling dekat secara lalai. Contoh fungsi ini adalah:

Dapat melayani anda: Berapa kesepuluh di dalam satu unit?

[[+3.7]] = 3

[[-1.5]] = -2

[[π]] = 3

Kedua -dua fungsi ini berterusan kecuali nombor keseluruhan, di mana lompatan dibentangkan, dan ia tetap untuk nilai -nilai antara bilangan bulat k dan k+1.

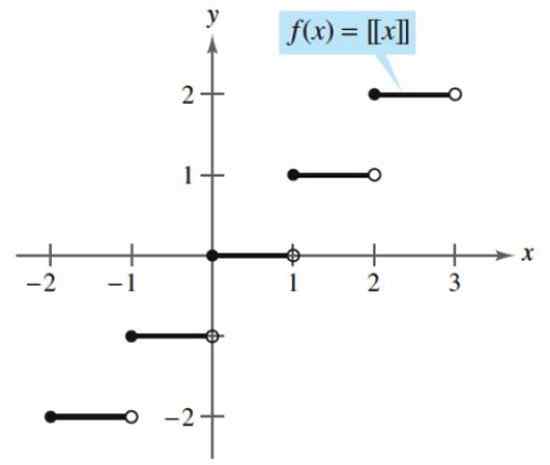Rajah 3. Fungsi lantai atau tanah. Sumber: Larson, r. Pengiraan pemboleh ubah.

- Contoh 2

Di bandar kadar teksi adalah 3.$ 65, untuk 100 m pertama. Dan untuk setiap 100 m adalah 0.$ 18, sebagai had setiap laluan 50 km.

Adalah dikehendaki untuk menubuhkan fungsi yang mengaitkan laluan dalam meter dengan kos perkhidmatan dengan $, yang mesti mempunyai bentuk ini:

f (x) = 3.65 + 0.18. [[x /100]] $

Di mana fungsi keseluruhan bahagian boleh berfungsi langit, yang mana kadar asasnya ditambahkan.$ 65. Contohnya, jika kita ingin tahu berapa banyak yang akan dibayar untuk perjalanan 6.25 km = 6250 m, kita akan mempunyai:

f (x) = 3.65 + 0.18. [[x /100]] $ = 3.65 + 0.18 . [[6250/100]] $ = 3.65 + [[11.25]] $ = 15.$ 65

Jika syarikat teksi memilih fungsi lantai, maka pelanggan akan membayar sedikit kurang untuk perjalanan:

f (x) = 3.65 + 0.18. [[x /100]] $ = 3.65 + 0.18 . [[6250/100]] $ = 3.65 + [[11.25]] $ = 14.$ 65

Latihan yang diselesaikan

- Latihan 1

Panggilan jarak jauh antara bandar a dan b kos 0.40 $ 10 minit. Selepas tempoh itu, pecahan atau minit tambahan bernilai 0.05 $.

Menyatakan kos c (t) panggilan yang berlangsung sejumlah minit.

Penyelesaian

Kami dapat menyatakan fungsi ini jika kita menganalisis apa yang berlaku dengan setiap pilihan untuk tempoh panggilan:

Untuk t ≤ 10 minit

Apabila t, yang merupakan masa panggilan yang berlangsung, kurang dari atau sama dengan 10 minit, dibayar 0.$ 40.

Boleh melayani anda: 2 -bahagian yang diselesaikan

Oleh itu:

f (t) = 0.$ 40 untuk t termasuk antara 0 dan 10 minit.

Kami sudah mempunyai bahagian fungsi.

Untuk t> 10 minit

Kes entero t

Sekarang mari kita lihat apa yang berlaku apabila masa t = 10 minit melebihi: mungkin berlaku bahawa lebihan adalah integer, contohnya perbualan berlangsung tepat 11, 12, 13, 14 minit atau lebih. Dalam hal ini jumlah panggilan akan:

f (t) = 0.40 + 0.05 (t-10) $, untuk t lebih daripada 10 minit, dengan keseluruhan t.

Iaitu dalam kes ini: t = 11, 12, 13, 14, 15 ... minit.

Sebagai contoh, katakan perbualan berlangsung tepat 15 minit, kosnya akan:

F (15) = 0.40 + 0.05 (15-10) $ = 0.$ 65

Kes perpuluhan

Akhirnya, pertimbangkan kes di mana panggilan berlangsung selama satu masa dengan bahagian perpuluhan. Contohnya, katakan bahawa panggilan berlangsung selama 15 minit dan 45 saat, yang akan menjadi decimally 15.75 minit.

Kami dapat menyatakannya dari segi seluruh bahagian jenis lantai, dengan mengandaikan bahawa syarikat itu ingin memberi lebih banyak faedah kepada pelanggan, atau langit:

f (t) = 0.40 + 0.05 ⋅ [[T-9]] $

Mari kita lihat apa yang akan dibayar oleh pelanggan jika ia berfungsi:

F (15.75) = 0.40 + 0.05 ⋅ [[15.75-9]] $ = 0.40 + 0.05 ⋅ [[6.75]] $ = 0.40 + 0.05 × 6 $ = 0.$ 70.

Atau sebagai fungsi langit, dalam hal ini kosnya:

F (15.75) = 0.40 + 0.05 [[15.75-9]] $ = 0.40 + 0.05 ⋅ [[6.75]] $ = 0.40 + 0.05 × 7 $ = 0.75 $.

Fungsi dan grafik

Sebagai fungsi yang ditakrifkan oleh bahagian adalah:

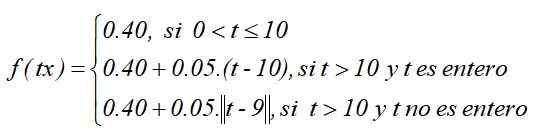
Grafik fungsi seperti ini, dengan mengandaikan bahawa fungsi jenis siling keseluruhan dipilih:

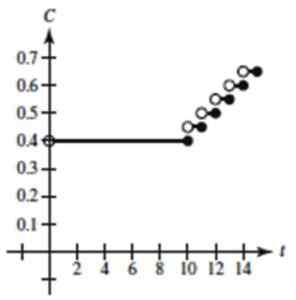Rajah 4. Graf fungsi melangkah latihan diselesaikan 1. Sumber: Larson, r. Pengiraan pemboleh ubah.

- Latihan 2

Kirakan integral ∫s (x) dx antara -3 dan 3 fungsi melangkah:

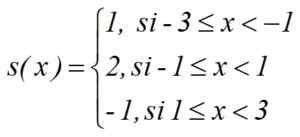
Penyelesaian

Kami menggunakan definisi untuk integral fungsi yang berperingkat:

Oleh itu, integral dicari saya adalah:

I = 1. [(-1)-(-3)] + 2.[1- (-1)]+(-1).[3-1] = 2+4-2 = 4

Rujukan

1. Jiménez, r. 2006.Fungsi matematik. Pendidikan Pearson.
2. Larson, r. 2010. Pengiraan pemboleh ubah. 9NA. Edisi. McGraw Hill.
3. Matematik iv. Fungsi. Pulih dari: Cobaqroo.Edu.mx.
4. Wikipedia. Keseluruhan fungsi bahagian. Pulih dari: Adakah.Wikipedia.org.
5. Wikipedia. Fungsi terhuyung -huyung. Pulih dari: Adakah.Wikipedia.org.